7_3 分数拆分（UVa10976）<缩小枚举范围>

每一个（k>0）这种形式的分数我们总是可以找到2个正整数x和y（x >= y），使得：
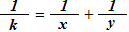
现在我们的问题是：给你k，请你写一个程序找出所有的x和y。
Input
输入含有多组测试数据（不会超过100组）。每组测试数据一列，有1个正整数k（0 < k <= 10000）。
Output
对每一组测试数据输出一列，输出共有多少组（x，y），然后输出这些解答。输出格式请参考Sample Output。

Sample Input
2
12

Sample Output

2
1/2 = 1/6 + 1/3
1/2 = 1/4 + 1/4
8
1/12 = 1/156 + 1/13
1/12 = 1/84 + 1/14
1/12 = 1/60 + 1/15
1/12 = 1/48 + 1/16
1/12 = 1/36 + 1/18
1/12 = 1/30 + 1/20
1/12 = 1/28 + 1/21
1/12 = 1/24 + 1/24