需求：

有时候当移动速度很慢，GPS定位的轨迹点就非常的多，这时候为了缩减数据量，需要将不突出的点去掉。

思路：

(1) 在曲线首尾两点间虚连一条直线,求出其余各点到该直线的距离。

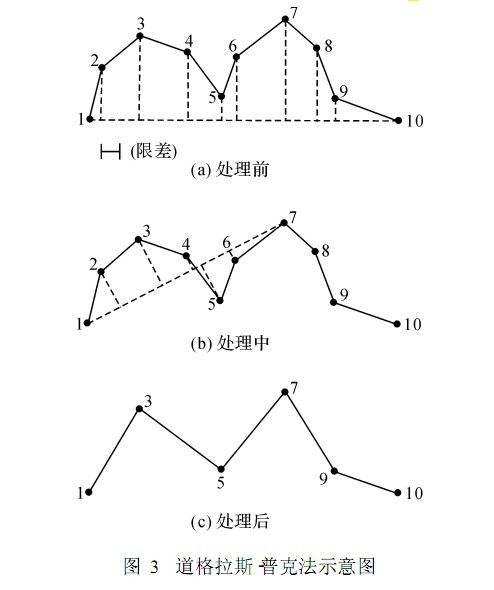
（2）选其最大者与阈值相比较,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点全部舍去。
（3）依据所保留的点,将已知曲线分成两部分处理,重复第1、2步操作，迭代操作，即仍选距离最大者与阈值比较,依次取舍,直到无点可舍去，最后得到满足给定精度限差的曲线点坐标

这里使用道格拉斯-普克算法实现，易于理解。效果对比图如下：

源代码：

<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">

<html xmlns="http://www.w3.org/1999/xhtml">

<head>

   <meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>

   <title>DouglasPeucker</title>

</head>

<body>

   <canvas id="drawing" style="height:300px;width:100%"></canvas>

    <canvas id="drawing2" style="height:300px;width:100%"></canvas>

</body>

<script type="text/javascript" >

    var points1=[];

    var pointsshao=[];

    var pts=[];

    var hval=30;//阈值

    //随机生成1000个点

    for(var i=0;i<1000;i++){

    var  oldx=i*10,oldy=Math.random()*150;

      points1.push([oldx,oldy,i]);

    }

    //求斜率

    function xielv(pt1,pt2)

    {

      var k,b;

      var canshu={};

      canshu.k=(pt1[1]-pt2[1])/(pt1[0]-pt2[0]);

      canshu.b=pt1[1]-canshu.k*pt1[0];

      return canshu;

    }

    //求点到直线的距离

    function distanceToline(pt,cs){

       return (Math.abs(cs.k*pt[0]-pt[1]+cs.b))/Math.sqrt(cs.k*cs.k+1);

    }

    //开始计算(道格拉斯普克算法)

    pts.push(points1[0]);

    countPoint(points1);

    pts.push(points1[points1.length-1]);

    //排序

    function sort(pts){

      for(var i=0;i<pts.length-1;i++)

      {

         var a=pts[i];

         var b=pts[i+1];

         if(b[2]>a[2]){

         pts[i]=b;

         pts[i+1]=a;

         for(var j=i;j>0;j--)

         {

             var c=pts[j-1];

             if(b[2]>c[2]){

               pts[j-1]=b;

               pts[j]=c;

             }

         }

         }

      }

    }

  //对坐标点进行取舍

 function countPoint(points){

       var maxD=0;

       var maxPoint=null;

       var maxindex=0;

       //大于2个点才开始计算

       if(points.length>2){

             var pt1=points[0];

           var pt2=points[points.length-1];

           var cs=xielv(pt1,pt2);

           for(var i=0;i<points.length;i++){

             var pt=points[i];

             var dis=distanceToline(pt,cs);

            //判断该线段中是否有点到由该线段端点组成的直线的距离大于限值

             if(dis>maxD)

             {

               maxD=dis;

               maxPoint=pt;

               maxindex=i;

             }

           }

               if(maxD>hval) //如果最大值就从该点位置将线段进行切分

             {

                 var pts1=points.slice(maxindex);//中分末尾数组

                 var pts2=points.slice(0,maxindex+1);//中分前面数组

                if(pts1.length>2 && pts2.length>2)

                {

                 if(!countPoint(pts1) && !countPoint(pts2)){  //如果两个线段都没有超过限制就结束计算

                   pts.push(maxPoint);

                 }

                }else if(pts1.length>2 && pts2.length<=2){ //计算pts1

                    if(!countPoint(pts1))pts.push(maxPoint);

                }else if(pts1.length<=2 && pts2.length>2){ //计算pts2

                   if(! countPoint(pts2))pts.push(maxPoint);

                }

             } return false;

       }

     }

    //由大到小

    sort(pts);

    drawWay("drawing2",pts);

    drawWay("drawing",points1)
    //绘制曲线

    function drawWay(name,points){

      var drawing=document.getElementById(name);

      if(drawing.getContext){

        var context=drawing.getContext("2d");

        context.beginPath();

        var oldx=points[0][0];

        var oldy=points[0][1];

        for(var i=0;i<points.length;i++){

          var p=points[i];

          context.moveTo(oldx,oldy);

          oldx=p[0];

          oldy=p[1];

          context.lineTo(oldx,oldy);

       }

       context.closePath();

       context.stroke();

    }

}

</script>

道格拉斯-普克算法（JavaScript实现）的更多相关文章

  1. OpenCV 学习笔记03 凸包convexHull、道格拉斯-普克算法Douglas-Peucker algorithm、approxPloyDP 函数

    凸形状内部的任意两点的连线都应该在形状里面. 1 道格拉斯-普克算法 Douglas-Peucker algorithm 这个算法在其他文章中讲述的非常详细,此处就详细撰述. 下图是引用维基百科的.ε ...

  2. GIS矢量数据化简：一种改进的道格拉斯-普克算法以及C++实现

    GIS领域的同志都知道,传统的道格拉斯-普克算法都是递归实现.然而有时候递归的层次太深的话会出现栈溢出的情况.在此,介绍一种非递归的算法. 要将递归算法改为非递归算法,一般情况下分为两种场景.第一种是 ...

  3. 道格拉斯—普克(Douglas一Peukcer)节点抽稀算法

    Douglas一Peukcer算法由D.Douglas和T.Peueker于1973年提出,简称D一P算法,是眼下公认的线状要素化简经典算法.现有的线化简算法中,有相当一部分都是在该算法基础上进行改进 ...

  4. .net中使用 道格拉斯-普特 抽希轨迹点

    Douglas一Peukcer算法由D.Douglas和T.Peueker于1973年提出,简称D一P算法,是目前公认的线状要素化简经典算法.现有的线化简算法中,有相当一部分都是在该算法基础上进行改进 ...

  5. 数据结构与算法JavaScript (一) 栈

    序 数据结构与算法JavaScript这本书算是讲解得比较浅显的,优点就是用javascript语言把常用的数据结构给描述了下,书中很多例子来源于常见的一些面试题目,算是与时俱进,业余看了下就顺便记录 ...

  6. 《数据结构与算法JavaScript描述》

    <数据结构与算法JavaScript描述> 基本信息 作者: (美)Michael McMillan 译者: 王群锋 杜欢 丛书名: 图灵程序设计丛书 出版社:人民邮电出版社 ISBN:9 ...

  7. 翻阅《数据结构与算法javascript描述》--数组篇

    导读: 这篇文章比较长,介绍了数组常见的操作方法以及一些注意事项,最后还有几道经典的练习题(面试题). 数组的定义: JavaScript 中的数组是一种特殊的对象,用来表示偏移量的索引是该对象的属性 ...

  8. 数据结构与算法javascript描述

    <数据结构与算法javascript描述>--数组篇 导读: 这篇文章比较长,介绍了数组常见的操作方法以及一些注意事项,最后还有几道经典的练习题(面试题). 数组的定义: JavaScri ...

  9. 列表的实现-----数据结构与算法JavaScript描述 第三章

    实现一个列表 script var booklist = new List(); booklist.append('jsbook'); booklist.append('cssbook'); book ...

随机推荐

  1. 2006年NOIP普及组复赛题解

    题目涉及算法: 明明的随机数:简单模拟: 开心的金明:01背包: Jam的计数法:模拟: 数列:二进制. 明明的随机数 题目链接:https://www.luogu.org/problem/P1059 ...

  2. hdu 4394 Digital Square（bfs）

    Digital Square Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)To ...

  3. TensorFlow指定使用GPU 多块gpu

    持续监控GPU使用情况命令: $ watch -n 10 nvidia-smi1一.指定使用某个显卡如果机器中有多块GPU,tensorflow会默认吃掉所有能用的显存, 如果实验室多人公用一台服务器 ...

  4. linux的iptables和firewall的区别

    firewall是centos7里面的新的防火墙命令,它底层还是使用 iptables 对内核命令动态通信包过滤的,简单理解就是firewall是centos7下管理iptables的新命令 Linu ...

  5. Java开发之快捷键

    1.显示桌面快捷键:win+D或者右击状态栏,选择显示桌面. 2.UE编辑器:如果想把多行记录合并为一行,使用替换(Ctrl+R),查找里输入^p(代表回车换行符),替换为里什么都不填,替换位置选择所 ...

  6. js基础——面向对象（构造函数）

    1.面向对象:类的标志,通过类可创建多个具有相同属性和方法的对象 2.创建对象 1)工厂模式方式:避免重复实例化但未能解决识别问题  function boss(name, age) {       ...

  7. Error与Exception的区别,Java常见异常Execption总结

    错误和异常的区别(Error vs Exception) 错误和异常的区别(Error vs Exception) 今天面试问了这样一个问题,"Error" 和 "Exc ...

  8. 2018-2-13-win10-uwp-图标制作器

    title author date CreateTime categories win10 uwp 图标制作器 lindexi 2018-2-13 17:23:3 +0800 2018-2-13 17 ...

  9. C#反射与特性(一)：反射基础

    目录 C#反射与特性(一):反射基础 1. 说明 1.1 关于反射.特性 2. 程序集操作 2.1 获取 程序集对象(Assembly) 2.2 Assembly 使用 2.3 获取程序集的方式 C# ...

  10. 银川区域赛 H道路与航线（原题啊）

    按照<算法竞赛进阶指南>写的 哦对了,注意下最后判断,因为开始拓扑的时候,s可能不在里边,所以不一定等于INF,而是应该大于等于INF #include<cstring> #i ...