FFT

study from:

http://www.orchidany.cf/2019/02/19/FFT1/

https://www.cnblogs.com/zwfymqz/p/8244902.html

e^iθ=cosθ+isinθ

重新写了一遍……

A(x)=F(x)*G(x)

F(x),G(x),A(x)分别为n,m,n+m次多项式

对于任意x，A(x),F(x),G(x)都是一个特定的数值。

F(x),G(x)为什么可以进行系数表示法和点值表示法的互换?

因为它们是k次多项式，如使用拉格朗日插值多项式从点值表示法转换为系数表示法。

对于A(x)，同样也是如此！

为什么可以进行F(x)*G(x)点值的相乘呢？

1.无论x为多少，A(x)都等于F(x)*G(x)

2.A(x)可以用点值表示，它是n+m次多项式（感觉说了句无用的话）

那需要多少个F(x)和G(x)点值的相乘呢？

由于A(x)是n+m次多项式，则F(x),G(x)至少各需要n+m+1个点值

得到的是n+m+1个点值，然后点值表示法转系数表示法，求出A(x)这个n+m次多项式的所有系数。

关于蝴蝶操作（迭代实现）

最后的编号（一种规则）->起始

两个位置在原位置上的改动

区间1->2->4->...

P3803 【模板】多项式乘法（FFT）

 #include <cstdio>

 #include <cstdlib>

 #include <cmath>

 #include <cstring>

 #include <string>

 #include <algorithm>

 #include <iostream>

 using namespace std;

 #define ll long long

 const double eps=1e-;

 const ll inf=1e9;

 const ll mod=1e9+;

 const int maxn=(1e6+)*; ///注意乘4[(n+m)*2]

 const double pi=acos(-);

 struct complex

 {

     double x,y;

     complex()

     {

     }

     complex(double x,double y)

     {

         this->x=x;

         this->y=y;

     }

     void init(double x,double y)

     {

         this->x=x;

         this->y=y;

     }

     complex operator+(const complex &b) const

     {

         return complex(x+b.x , y+b.y);

     }

     complex operator-(const complex &b) const

     {

         return complex(x-b.x , y-b.y);

     }

     complex operator*(const complex &b) const

     {

         return complex(x*b.x-y*b.y , x*b.y+y*b.x);

     }

 }a[maxn],b[maxn];

 int r[maxn],n,m,tot;

 void fft(complex a[maxn],int mode)

 {

     int i,j,pre_siz,cur_siz;

     complex temp,value,x,y;

     for (i=;i<tot;i++)

         if (i<r[i]) ///just change one time

             swap(a[i],a[r[i]]);

     for (pre_siz=;pre_siz<tot;pre_siz<<=)

     {

         cur_siz=pre_siz<<;

         /// 2pi/cur_siz = pi/pre_siz

         temp.init(cos(pi/pre_siz),mode*sin(pi/pre_siz));

         for (i=;i<tot;i+=cur_siz)

         {

             value.init(,);

             for (j=;j<pre_siz;j++,value=value*temp)

             {

                 x=a[i+j],y=value*a[i+pre_siz+j];

                 a[i+j]=x+y;

                 a[i+pre_siz+j]=x-y;

             }

         }

     }

 }

 int main()

 {

     int i,nm,len;

     scanf("%d%d",&n,&m);

     for (i=;i<=n;i++)

         scanf("%lf",&a[i].x);

     for (i=;i<=m;i++)

         scanf("%lf",&b[i].x);

     nm=n+m;

     tot=,len=;

     while (tot<=nm)  ///2^len not less than n+m+1

     {

         tot<<=;

         len++;

     }

     ///关系 ......

     for (i=;i<tot;i++)

         r[i]=(r[i>>]>>) | ((i&)<<(len-));

     ///系数表示法转点值表示法

     fft(a,);

     fft(b,);

     ///a,b点值相乘

     for (i=;i<tot;i++)

         a[i]=a[i]*b[i];

     ///点值表示法转系数表示法，恰巧为......

     fft(a,-);

     for (i=;i<=nm;i++) ///n+m

         ///点值表示法转系数表示法，要除以的系数

         printf("%lld%c",(ll)(a[i].x/tot+0.5),i==tot?'\n':' ');  /// /tot

     return ;

 }

P1919 【模板】A*B Problem升级版（FFT快速傅里叶）

 #include <cstdio>

 #include <cstdlib>

 #include <cmath>

 #include <cstring>

 #include <string>

 #include <algorithm>

 #include <iostream>

 using namespace std;

 #define ll long long

 const double eps=1e-;

 const ll inf=1e9;

 const ll mod=1e9+;

 const int maxn=(1e6+)*; ///注意乘4[(n+m)*2]

 const double pi=acos(-);

 struct complex

 {

     double x,y;

     complex()

     {

     }

     complex(double x,double y)

     {

         this->x=x;

         this->y=y;

     }

     void init(double x,double y)

     {

         this->x=x;

         this->y=y;

     }

     complex operator+(const complex &b) const

     {

         return complex(x+b.x , y+b.y);

     }

     complex operator-(const complex &b) const

     {

         return complex(x-b.x , y-b.y);

     }

     complex operator*(const complex &b) const

     {

         return complex(x*b.x-y*b.y , x*b.y+y*b.x);

     }

 }a[maxn],b[maxn];

 int r[maxn],n,m,tot,z[maxn];

 char str[maxn];

 void fft(complex a[maxn],int mode)

 {

     int i,j,pre_siz,cur_siz;

     complex temp,value,x,y;

     for (i=;i<tot;i++)

         if (i<r[i]) ///just change one time

             swap(a[i],a[r[i]]);

     for (pre_siz=;pre_siz<tot;pre_siz<<=)

     {

         cur_siz=pre_siz<<;

         /// 2pi/cur_siz = pi/pre_siz

         temp.init(cos(pi/pre_siz),mode*sin(pi/pre_siz));

         for (i=;i<tot;i+=cur_siz)

         {

             value.init(,);

             for (j=;j<pre_siz;j++,value=value*temp)

             {

                 x=a[i+j],y=value*a[i+pre_siz+j];

                 a[i+j]=x+y;

                 a[i+pre_siz+j]=x-y;

             }

         }

     }

 }

 int main()

 {

     int i,nm,len;

     scanf("%d",&n); ///输入样例有毒，n后面有空格

     n--;

     scanf("%s",str);

     for (i=;i<=n;i++)

         a[n-i].x=str[i]-;

     scanf("%s",str);

     for (i=;i<=n;i++)

         b[n-i].x=str[i]-;

     nm=n+n;

     tot=,len=;

     while (tot<=nm)  ///2^len not less than n+m+1

     {

         tot<<=;

         len++;

     }

     ///关系 ......

     for (i=;i<tot;i++)

         r[i]=(r[i>>]>>) | ((i&)<<(len-));

     ///系数表示法转点值表示法

     fft(a,);

     fft(b,);

     ///a,b点值相乘

     for (i=;i<tot;i++)

         a[i]=a[i]*b[i];

     ///点值表示法转系数表示法，恰巧为......

     fft(a,-);

     for (i=;i<=nm;i++)

     {

         ///点值表示法转系数表示法，要除以的系数

         z[i]+=a[i].x/tot+0.5;

 //        printf("%d ",a[i].x/tot+0.5);

         if (z[i]>=)

         {

             z[i+]+=z[i]/;

             z[i]%=;

         }

         else if (z[i]<)

         {

             z[i+]+=z[i]/-(z[i]!=);

             z[i]=(z[i]%+)%;

         }

     }

     while (z[i]>=)

     {

         z[i+]=z[i]/;

         z[i]%=;

         i++;

     }

     ///输入的都是正整数

     ///前导0

     while (z[i]==)

         i--;

     while (i>=)

         printf("%d",z[i--]);

     ///也可以认为结果是a[0]+a[1]*10+a[2]*10^2+...

     return ;

 }

 /*

 2

 12

 13

 2

 99

 99

 3

 199

 299

 10

 9789344841

 4839019669

 另外的提高速度的方法：

 压位

 结果为：

 a[0]+a[1]*x+a[2]*x^2

 x=10^k

 */

==================================================

NTT

https://www.cnblogs.com/Wuweizheng/p/8553155.html

百度“原根”

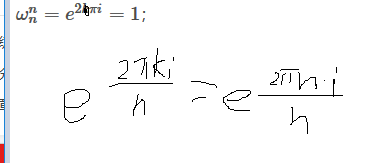
对于选取的P，可用的n最大的值与P中的2的系数有关

如选择998244353就优于1004535809。

如果选择框住的三个数，那么可以处理的最大的n+m为2^23=8388608。

最好模数对应的g(底数，最后一列)都相同，否则对于不同的模数，要选择不同的g。

如果题目要求除以998244353之类的满足条件的数，则可以直接用这个方法做，不用后续处理

P1919 【模板】A*B Problem升级版（FFT快速傅里叶）

结果小于等于

9[第一个数每一位的最大值]*9[第二个数每一位的最大值]*n[两个数的最大长度] = 4860000

可以使用取模998244353

 #include <cstdio>

 #include <cstdlib>

 #include <cmath>

 #include <cstring>

 #include <string>

 #include <algorithm>

 #include <iostream>

 using namespace std;

 #define ll long long

 const double eps=1e-;

 const ll inf=1e9;

 const ll mod=;

 const int maxn=(1e5+)*;

 ll di=;

 int tot,r[maxn];

 ll a[maxn],b[maxn],inv_siz[],inv_rev_siz[],c[maxn];

 char str[maxn];

 ll mul(ll a,ll b)

 {

     ll y=;

     while (b)

     {

         if (b&)

             y=y*a%mod;

         a=a*a%mod;

         b>>=;

     }

     return y;

 }

 void ntt(ll a[maxn],int mode)

 {

     int i,j,cnt_pre,cnt_cur,siz;

     ll x,y,sing,value;

     for (i=;i<tot;i++)

         if (i<r[i])

             swap(a[i],a[r[i]]);

     for (cnt_pre=,siz=;cnt_pre<tot;cnt_pre=cnt_pre<<,siz++)  ///

     {

         cnt_cur=cnt_pre<<;

         sing=mode==?inv_siz[siz]:inv_rev_siz[siz];

         for (i=;i<tot;i+=cnt_cur)

         {

             value=;

             for (j=;j<cnt_pre;j++,value=value*sing%mod)

             {

                 x=a[i+j],y=value*a[i+j+cnt_pre]%mod;

                 a[i+j]=(x+y)%mod;

                 a[i+j+cnt_pre]=(x-y+mod)%mod;

             }

         }

     }

 }

 int main()

 {

     int n,m,len,nm,i,j;

  //    scanf("%d%d%d",&n,&m,&p);

 //    for (i=0;i<=n;i++)

 //        scanf("%lld",&a[i]);

 //    for (i=0;i<m;i++)

 //        scanf("%lld",&b[i]);

     scanf("%d",&n);

     n--;

     scanf("%s",str);

     for (i=;i<=n;i++)

         a[i]=str[n-i]-;

     scanf("%s",str);

     for (i=;i<=n;i++)

         b[i]=str[n-i]-;

     nm=n+n;

     tot=,len=;

     while (tot<=nm)

     {

         tot<<=;

         len++;

     }

     for (i=;i<tot;i++)

         r[i]=(r[i>>]>>) | ((i&)<<(len-));

     for (i=,j=;i<=tot;i=i<<,j++) ///

     {

         inv_siz[j]=mul(di,(mod-)/i);

         inv_rev_siz[j]=mul(di,(mod-)-(mod-)/i);

     }

     ntt(a,);

     ntt(b,);

     for (i=;i<tot;i++)

         a[i]=a[i]*b[i]%mod;

     ntt(a,-);

     j=mul(tot,mod-);

     for (i=;i<=nm;i++)

     {

         a[i]=a[i]*j%mod;

         c[i]+=a[i];

         if (c[i]>=)

         {

             c[i+]+=c[i]/;

             c[i]%=;

         }

         else if (c[i]<)

         {

             c[i+]+=c[i]/-(c[i]!=);

             c[i]=(c[i]%+)%;

         }

     }

     while (c[i]>=)

     {

         c[i+]=c[i]/;

         c[i]%=;

         i++;

     }

     while (c[i]==)

         i--;

     while (i>=)

         printf("%lld",c[i--]);

     return ;

 }

 /*

 1

 8

 9

 2

 12

 13

 2

 99

 99

 3

 111

 111

 3

 999

 102

 101898

 */

感觉别人的代码短很多：

https://www.bbsmax.com/A/ke5jRWmO5r/

mode=-1下不同的实现方法

reverse(&a[1],&a[limit]);

P4245 【模板】任意模数NTT

https://www.luogu.org/problemnew/solution/P4245

https://www.cnblogs.com/Memory-of-winter/p/10223844.html

这样写的前提是取模的数之间互质，才能使用inv(模数) [inv 指的是 求逆]

可以理解为k1''=k1'+g*B

x1+k1''A=x1+(k1'+g*B)*A=(x1+k1'*A)+g*A*B

======================================

max = 10^9 * 10^9 * 10^5 = 10^23

对应若干个模数的相等大于它

 #include <cstdio>

 #include <cstdlib>

 #include <cmath>

 #include <cstring>

 #include <string>

 #include <algorithm>

 #include <iostream>

 using namespace std;

 #define ll long long

 const double eps=1e-;

 const ll inf=1e9;

 const int maxn=(1e5+)*;

 ll chu[]={,,};  ///single>10^8 all>10^24

 ll di=,mod,re[][maxn];

 int tot,r[maxn];

 ll a[maxn],b[maxn],aa[maxn],bb[maxn],inv_siz[],inv_rev_siz[],c[maxn];

 ll mul(ll a,ll b)

 {

     ll y=;

     while (b)

     {

         if (b&)

             y=y*a%mod;

         a=a*a%mod;

         b>>=;

     }

     return y;

 }

 ll _mul(ll a,ll b,ll c)

 {

     ll y=;

     while (b)

     {

         if (b&)

             y=y*a%c;

         a=a*a%c;

         b>>=;

     }

     return y;

 }

 void ntt(ll a[maxn],int mode)

 {

     int i,j,cnt_pre,cnt_cur,siz;

     ll x,y,sing,value;

     for (i=;i<tot;i++)

         if (i<r[i])

             swap(a[i],a[r[i]]);

     for (cnt_pre=,siz=;cnt_pre<tot;cnt_pre=cnt_pre<<,siz++)  ///

     {

         cnt_cur=cnt_pre<<;

         sing=mode==?inv_siz[siz]:inv_rev_siz[siz];

         for (i=;i<tot;i+=cnt_cur)

         {

             value=;

             for (j=;j<cnt_pre;j++,value=value*sing%mod)

             {

                 x=a[i+j],y=value*a[i+j+cnt_pre]%mod;

                 a[i+j]=(x+y)%mod;

                 a[i+j+cnt_pre]=(x-y+mod)%mod;

             }

         }

     }

 }

 int main()

 {

     int n,m,len,nm,i,j,k;

     ll p;

     scanf("%d%d%lld",&n,&m,&p);

     for (i=;i<=n;i++)

     {

         scanf("%lld",&aa[i]);

         aa[i]%=p;

     }

     for (i=;i<=m;i++)

     {

         scanf("%lld",&bb[i]);

         bb[i]%=p;

     }

     nm=n+m;

     tot=,len=;

     while (tot<=nm)

     {

         tot<<=;

         len++;

     }

     for (i=;i<tot;i++)

         r[i]=(r[i>>]>>) | ((i&)<<(len-));

     for (k=;k<;k++)

     {

         memcpy(a,aa,sizeof(aa));

         memcpy(b,bb,sizeof(bb));

         ///最主要觉得一起写在ntt函数中，不好改

         mod=chu[k];

         for (i=,j=;i<=tot;i=i<<,j++) ///

         {

             inv_siz[j]=mul(di,(mod-)/i);

             inv_rev_siz[j]=mul(di,(mod-)-(mod-)/i);

         }

         ntt(a,);

         ntt(b,);

         for (i=;i<tot;i++)

             a[i]=a[i]*b[i]%mod;

         ntt(a,-);

         j=mul(tot,mod-);

         for (i=;i<=nm;i++)

             re[k][i]=a[i]*j%mod;

     }

     /**

     取模的数之间，gcd(mod1,mod2)=1

     **/

     ll x1,x2,x3,x4,A,B,C,k1,k4;

     for (j=;j<=nm;j++)

     {

         x1=re[][j],x2=re[][j],x3=re[][j];

         A=chu[],B=chu[],C=chu[];

         k1=(((x2-x1)%B+B)%B)*_mul(A,B-,B)%B;

         x4=x1+k1*A;

         k4=(((x3-x4)%C+C)%C)*_mul(A*B%C,C-,C)%C;   ///(...%C+C)%C

         printf("%lld%c",(x4%p+k4%p*A%p*B%p)%p,j==nm?'\n':' '); ///k4%p, since k4>p

         ///it is safe that x4%p

         ///之后则是((x4-x5+D)%D)*mul(A*B%D*C%D,D-2,D)%D;

     }

     return ;

 }

 /*

 1 1 10001

 1000000000 1000000000

 1000000000 1000000000

 1 2 10001

 1000000000 1000000000

 1000000000 1000000000 1000000000

 5 6 1000000009

 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000

 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000

 */

看毛啸《再探快速傅里叶变换》

题目练习：

[SDOI2015]序列统计

==================================================

分治FFT

P4721 【模板】分治 FFT

https://blog.csdn.net/VictoryCzt/article/details/82939586

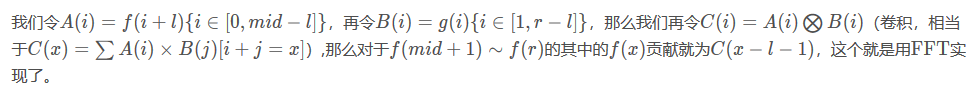
其实，C(x)是多算了一些内容，C(0)~C(mid-l-1)是无用的，但是没办法。

(r-mid)+(r-mid-1)+...+1 -> FFT len=大于等于r-l的最小的数，O(len*log(len))。

对于f(x) 其它数1-~x-1对f(x)的贡献，

通过cdq处理

类似的题 https://www.cnblogs.com/cmyg/p/11146038.html

 #include <cstdio>

 #include <cstdlib>

 #include <cmath>

 #include <cstring>

 #include <string>

 #include <algorithm>

 #include <iostream>

 using namespace std;

 #define ll long long

 const double eps=1e-;

 const ll inf=1e9;

 const ll mod=;

 const int maxn=(1e5+)*;

 ll f[maxn],g[maxn],a[maxn],b[maxn];

 ll inv_di[],inv_rev_di[],inv_tot[];

 int tot,ind[maxn];

 ll di=;

 ll mul(ll a,ll b)

 {

     ll y=;

     while (b)

     {

         if (b&)

             y=y*a%mod;

         a=a*a%mod;

         b>>=;

     }

     return y;

 }

 void ntt(ll *a,int mode)

 {

     int i,j,cnt_pre,cnt_cur,cnt=;

     ll sing,value,x,y;

     for (i=;i<tot;i++)

         if (i<ind[i])

             swap(a[i],a[ind[i]]);

     for (cnt_pre=,cnt=;cnt_pre<tot;cnt_pre<<=,cnt++)

     {

         cnt_cur=cnt_pre<<;

         sing=mode==?inv_di[cnt]:inv_rev_di[cnt];

         for (i=;i<tot;i+=cnt_cur)

         {

             value=;

             for (j=;j<cnt_pre;j++,value=value*sing%mod)

             {

                 x=a[i+j],y=a[i+j+cnt_pre]*value%mod;

                 a[i+j]=(x+y)%mod;

                 a[i+j+cnt_pre]=(x-y+mod)%mod;

             }

         }

     }

 }

 void cdq(int l,int r)

 {

     if (l==r)

         return;

     int m=(l+r)>>,nm,len,i;

     cdq(l,m);

     /**

     对于[m+1,r],

     [l,m]对它们的贡献

     C(z)=f(l+x)*g(1+y)

     x in [0,m-l]

     y in [0,r-l-1]

     z=x+y

     [m-l,r-l-1]

     **/

     tot=,len=;

     nm=(m-l)+(r-l-);

     while (tot<=nm)

         tot<<=,len++;

     for (i=;i<tot;i++)

         ind[i]=(ind[i>>]>>) | ((i&)<<(len-));

     for (i=;i<=m-l;i++)

         a[i]=f[l+i];

     for (i=m-l+;i<tot;i++)

         a[i]=;

     for (i=;i<=r-l-;i++)

         b[i]=g[+i];

     for (i=r-l;i<tot;i++)

         b[i]=;

     ntt(a,);

     ntt(b,);

     for (i=;i<tot;i++)

         a[i]=a[i]*b[i]%mod;

     ntt(a,-);

     for (i=m-l;i<=r-l-;i++)

         (f[i+l+]+=a[i]*inv_tot[len])%=mod;

     cdq(m+,r);

 }

 int main()

 {

     int n,i,j;

     scanf("%d",&n);

     for (i=;i<n;i++)

         scanf("%lld",&g[i]);

     f[]=;

     for (i=,j=;i<=4e5;i<<=,j++)

     {

         inv_tot[j]=mul(i,mod-);

         inv_di[j]=mul(di,(mod-)/i);

         inv_rev_di[j]=mul(di,(mod-)-(mod-)/i);

     }

     cdq(,n);   ///begin from 0

     for (i=;i<n;i++)

         printf("%lld%c",f[i],i==n-?'\n':' ');

     return ;

 }

快速沃尔什变换 与 快速莫比乌斯变换
https://www.cnblogs.com/cmyg/p/10424145.html

FTT & NTT & 分治FFT的更多相关文章

  1. 洛谷.4721.[模板]分治FFT(NTT)

    题目链接 换一下形式:\[f_i=\sum_{j=0}^{i-1}f_jg_{i-j}\] 然后就是分治FFT模板了\[f_{i,i\in[mid+1,r]}=\sum_{j=l}^{mid}f_jg ...

  2. luoguP4721 【模板】分治 FFT (分治NTT)

    给定 $g[1....n-1]$,求 $f[0],f[1],...,f[n-1]$,其中   $f[i]=\sum_{j=1}^{i}f[i-j]g[j]$    变界为 $f[0]=1$ 答案模 9 ...

  3. 再探快速傅里叶变换(FFT)学习笔记(其三)(循环卷积的Bluestein算法+分治FFT+FFT的优化+任意模数NTT)

    再探快速傅里叶变换(FFT)学习笔记(其三)(循环卷积的Bluestein算法+分治FFT+FFT的优化+任意模数NTT) 目录 再探快速傅里叶变换(FFT)学习笔记(其三)(循环卷积的Blueste ...

  4. BNUOJ 51279[组队活动 Large](cdq分治+FFT)

    传送门 大意:ACM校队一共有n名队员,从1到n标号,现在n名队员要组成若干支队伍,每支队伍至多有m名队员,求一共有多少种不同的组队方案.两个组队方案被视为不同的,当且仅当存在至少一名队员在两种方案中 ...

  5. 【XSY2666】排列问题 DP 容斥原理 分治FFT

    题目大意 有\(n\)种颜色的球,第\(i\)种有\(a_i\)个.设\(m=\sum a_i\).你要把这\(m\)个小球排成一排.有\(q\)个询问,每次给你一个\(x\),问你有多少种方案使得相 ...

  6. 【XSY2887】【GDOI2018】小学生图论题 分治FFT 多项式exp

    题目描述 在一个 \(n\) 个点的有向图中,编号从 \(1\) 到 \(n\),任意两个点之间都有且仅有一条有向边.现在已知一些单向的简单路径(路径上任意两点各不相同),例如 \(2\to 4\to ...

  7. 【XSY2744】信仰圣光 分治FFT 多项式exp 容斥原理

    题目描述 有一个\(n\)个元素的置换,你要选择\(k\)个元素,问有多少种方案满足:对于每个轮换,你都选择了其中的一个元素. 对\(998244353\)取模. \(k\leq n\leq 1525 ...

  8. 【BZOJ5119】【CTT2017】生成树计数 DP 分治FFT 斯特林数

    CTT=清华集训 题目大意 有\(n\)个点,点权为\(a_i\),你要连接一条边,使该图变成一颗树. 对于一种连边方案\(T\),设第\(i\)个点的度数为\(d_i\),那么这棵树的价值为: \[ ...

  9. 【XSY2166】Hope 分治 FFT

    题目描述 对于一个\(1\)到\(n\)的排列\(a_1,a_2,a_3,\ldots,a_n\),我们定义这个排列的\(P\)值和\(Q\)值: 对于每个\(a_i\),如果存在一个最小的\(j\) ...

随机推荐

  1. 2018-2-13-win10-uwp-hashcash

    title author date CreateTime categories win10 uwp hashcash lindexi 2018-2-13 17:23:3 +0800 2018-2-13 ...

  2. tomcat的首次登录配置

    登录tomcat时需要输入账号密码,而账号密码需要在配置文件中配置好才能使用. 此处我们先点击取消,tomcat会弹出一个提示界面: 这个界面的大致意思是: 401未经授权 您无权查看此页面. 如果您 ...

  3. {"timestamp":"2019-11-12T02:39:28.949+0000","status":415,"error":"Unsupported Media Type","message":"Content type 'text/plain;charset=UTF-8' not supported","path":&quo

    在Jmeter运行http请求时报错: {"timestamp":"2019-11-12T02:39:28.949+0000","status&quo ...

  4. laravel写crontab定时任务（发送邮件）和laravel crontab不执行的问题

    1.artisan命令: php artisan make:command SendRejectEmail 2.app/Console/Commands下就会看到SendRejectEmail.php ...

  5. SnowFlakeId 分布式雪花id算法

    package com.jn.baseservice.utils; import com.jn.baseservice.common.Number; import lombok.Getter; imp ...

  6. 分布式项目pom

    <dependencies> <dependency> <groupId>junit</groupId> <artifactId>junit ...

  7. elementUi-复选框，使用v-for循环出来的复选框,默认多个值为勾选状态

    1. 使用 v-model="BottomSelectFor[index].tick" 绑定要默认勾选的状态 2.在数组中定义 tick:true,没有的字段默认为false 3. ...

  8. AcWing 197. 阶乘分解 （筛法）打卡

    给定整数 N ,试把阶乘 N! 分解质因数,按照算术基本定理的形式输出分解结果中的 pipi 和 cici 即可. 输入格式 一个整数N. 输出格式 N! 分解质因数后的结果,共若干行,每行一对pi, ...

  9. [ZJOI2010]排列计数 题解

    Description 称一个1,2,...,N的排列P1,P2...,Pn是Magic的,当且仅当2<=i<=N时,Pi>Pi/2. 计算1,2,...N的排列中有多少是Magic ...

  10. 【C#技术】一篇文章搞掂：LLBL

    公司代码速查 ParameterBase.CurrentUser.UserId ICustomerDeskDetailManager customerDeskDetailManager = Clien ...