[Elementary Mechanics-01]Two masses and a spring

[Elementary Mechanics Using Python-01]

Question

5.28 Two masses and a spring. Two particles of m = 0.1 kg are attached with a spring with spring constant k = 100 N/m and equilibrium length b = 0.01 m. Both particles start at rest and the spring is at equilibrium. An external force F = 1000 N acts during 1 s on one of the particles in the direction of the other particle. Find the position of both particles as a function of time from the time t = 0 s when the external force starts acting. (You may solve this problem analytically or numerically).

设置变量

设前后两个质点的位移分别为\(x_1\),\(x_2\),时间为\(t_1\)。

列出质点的微分方程

\[\left\{
\begin{matrix}
m\frac{d^2}{dt^2}x_1 = F -k(x_1 - x_2 + b) \\
m\frac{d^2}{dt^w}x_2 = k(x_1 - x_2 + b)
\end{matrix}
\right.
\]

初始值

\[\left\{
\begin{matrix}
x_1(0) = 0 \\
x_2(0) = b \\
v_1(0) = 0 \\
v_2(0) = 0 \\
a_1(0) = \frac{F}{m} \\
a_2(0) = 0
\end{matrix}
\right.
\]

利用Python

// 引入库
import numpy as np
import matplotlib.pyplot as plt

// 定义常量
F = 1000
m = 0.1
k = 100
b = 0.01

// 建立时间Array
t = np.linspace(0, 1, 1000000)
// 设置时间间隔
dt = 1/1000000

// 两质点的运动量Array
x1 = np.zeros(1000000, dtype =float)
v1 = np.zeros(1000000, dtype =float)
a1 = np.zeros(1000000, dtype =float)
x2 = np.zeros(1000000, dtype =float)
v2 = np.zeros(1000000, dtype =float)
a2 = np.zeros(1000000, dtype =float)

// 初值条件
x1[0], v1[0], a1[0] = 0, 0, F/m
x2[0], v2[0], a2[0] = b, 0, 0

// 数值积分
for index in range(1, 1000000):
    // 质点1的微分方程
    a1[index] = (F - k*(x1[index-1] - x2[index-1] + b)) / m
    v1[index] = v1[index-1] + a1[index-1]*dt
    x1[index] = x1[index-1] + v1[index-1]*dt
    // 质点2的微分方程
    a2[index] = k*(x1[index-1] - x2[index-1] + b) / m
    v2[index] = v2[index-1] + a2[index-1]*dt
    x2[index] = x2[index-1] + v2[index-1]*dt
    // 弹性碰撞
    if x1[index] >= x2[index]:
        v1[index], v2[index] = v2[index], v1[index] 

// 画图
plt.title("b = {}".format(b))
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
plt.xlim([0, 1*1.1])
plt.xlabel("t(s)")
plt.ylim([0, 2500*1.1])
plt.ylabel("x(m)")
plt.plot(t, x1, label="x1(t)")
plt.plot(t, x2, label="x2(t)")
plt.legend()
plt.savefig("{0}.jpg".format(b))

我们看看随着b减小二者的运动变化

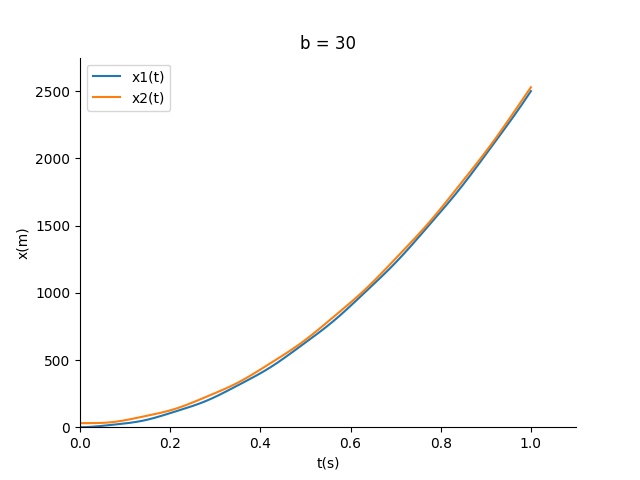
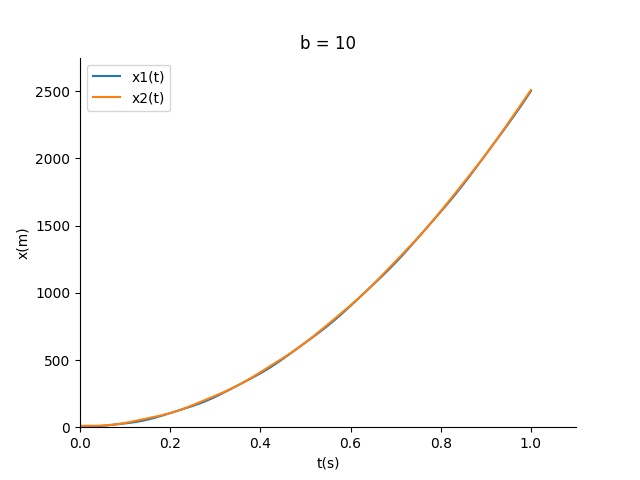
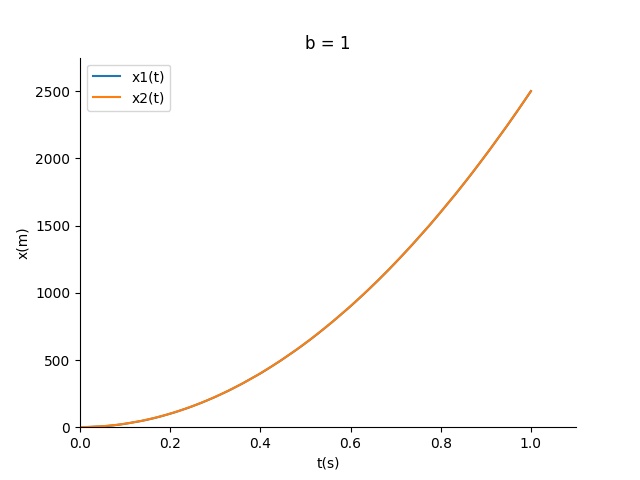
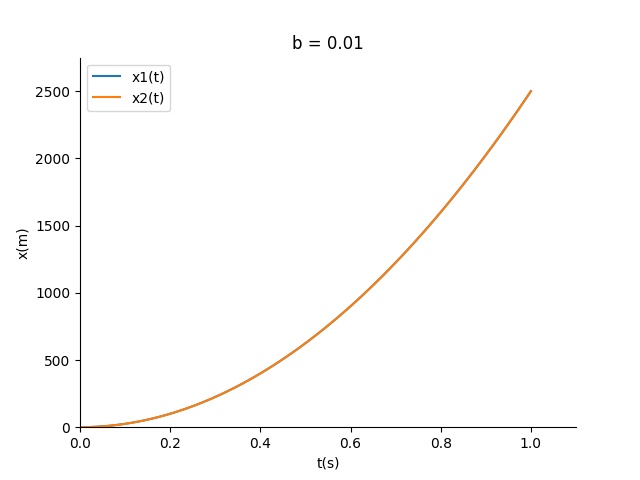
结论

显然b足够小，我们可以直接忽略弹簧和简谐运动带来的影响，因此有

\[x_1 = x_2 =
\left\{
\begin{matrix}
\frac{1}{2}\frac{F}{2m}t^2, 0 \leqslant t \leqslant 1s \\
\frac{1}{2}\frac{F}{2m}t_0^2 + \frac{F}{2m}t_0t, t \geqslant 1s
\end{matrix}
\right.
\]