LSM(Log Structured Merge Trees ) 笔记

一、大幅度制约存储介质吞吐量的原因
二、传统数据库的实现机制
三、LSM Tree的历史由来
四、提高写吞吐量的思路
- 4.1 一种方式是数据来后，直接顺序落盘
- 4.2 另一种方式，是保证落盘的数据是顺序写入的同时，还保证这些数据是有序的
五、 LSM Tree结构图
六、参考文献

一、大幅度制约存储介质吞吐量的原因

首先抛出结论。无论任何存储介质（不管是机械硬盘还是SSD，抑或是内存）的顺序访问速度都远远高出随机访问的速度。

二、传统数据库的实现机制

传统数据库，比如Mysql使用的b+树索引，对读友好。但容易造成随机写。比如新插入一个值到数据库，首先我们要读取b+树，判断新插入的值放在树的什么位置，其次在特定的位置写入新值，并做一系列调整，分裂，使之满足b+树的特性。这不可避免的造成了磁盘的随机访问，大数据量的插入速度很慢。当然这也符合历史发展趋势，早起的IT行业，数据量和数据增长速度有限，只要拥有良好的查询性能，即可满足需求。

但随着硬件性能的提升，业务形态的变化，现今的互联网系统，往往面临着数据的大量、高速产生。如何加快存储速度，成了关键。于是LSM Tree应运而生。

三、LSM Tree的历史由来

LSM Tree的最早概念，诞生于1996年google的“BigTable”论文。后世多种数据库产品对LSM Tree的具体实现，都有一些小的差异。采用LSM Tree作为存储结构的数据库有，Google的LevelDB, Facebook的RockDB(RockDB来源于LevelDB), Cassandra,HBase等。

四、提高写吞吐量的思路

既然顺序写比起随机写速度更快。那得想办法将数据顺序写。

4.1 一种方式是数据来后，直接顺序落盘

这拥有很高的写速度。但是当我们想要查寻一个数据的时候，由于存储下的数据本身是无序的（写的值本身无法控制顺序），无法使用任何算法进行优化，只能挨个查询，读取速度是很慢的。

4.2 另一种方式，是保证落盘的数据是顺序写入的同时，还保证这些数据是有序的

而请求写入的数据本身是无序且不可预测的，如何保证落盘的数据是有序的呢？这就需要利用内存访问速度比硬盘快的原理。将写入的请求，先在内存中缓存起来，按一定的有序结构组织，达到一定量后，再写入硬盘，从而使得硬盘顺序写入了有序的数据。提高数据的写入速度同时，方便了后续基于有序数据的查找(有序的数据结构，可以通过二分查找等算法进行进行快速查询，具体查找算法，得看是哪种有序结构)

五、 LSM Tree结构图

LSM tree即利用了上述第二种方式。具体结构图如下：

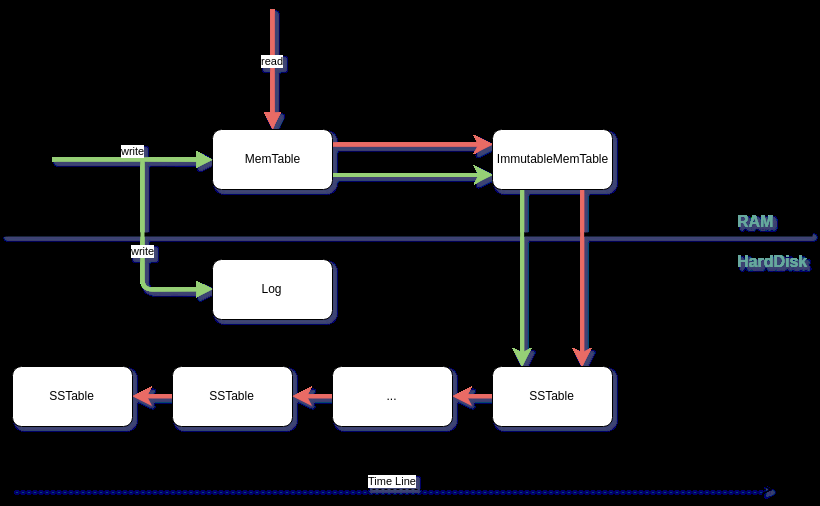
5.1 写入时，为什么要先写一份log

为了防止写入的数据，在断电时丢失。所以先顺序写一份log到硬盘，方便数据恢复。

5.2 什么是MemTable

写入数据的内存缓存，MemTable中存储的是有序的数据。什么才是有序的数据结构？不同的实现可能不相同。LevelDB使用的是SkipList。Hbase使用的是B Tree。

5.3 什么是ImmutableMemTable

MemTable中的数据随时在增加，当其增加到一定量后，将其变为不可变数据，ImmutableMemTable。新生成一份MemTable用于后续的数据写入。ImmutableMemTable中的数据，将被写入到硬盘中的SSTable.

5.4 什么是SSTable

SSTable 全称Sorted String Table。实际上就是被写入数据的有序存储文件，所以叫sorted.

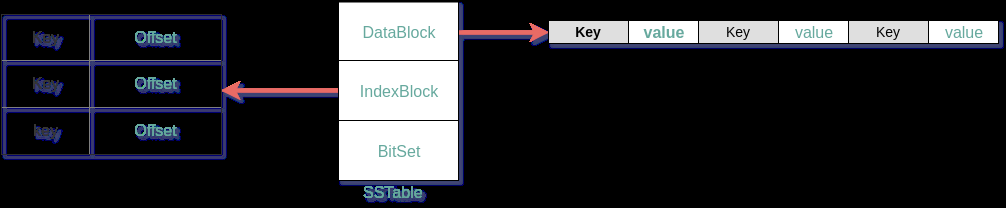
SSTable文件有DataBlock,IndexBlock,BitSet(不同的实现，有可能没有)

DataBlock 一个SSTable包含多个数据块，数据按KeyValue的形式有序组织。
IndexBlock 记录每个数据块中最大的那个Key的Offset
BitSet 使用Bloom Filter来将一个Key映射到BitSet中

数据的有序组织、IndexBlock、BitSet。这些数据结构，都是为了提高数据读取时的速度。那数据是如何进行读取的呢？

5.5 如何进行数据读取

读取的大概流程如下

由于SSTable是顺序创建，所以最新的SSTable中包含了最新的值。再查找SSTable时，依次查找最新的SSTable。

每一个SSTable的查询流程如下

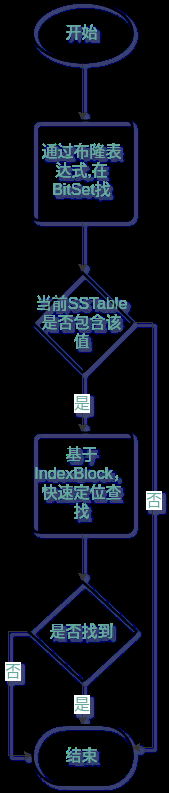
布隆表达式的原理是以极小的数据容量，去存储大量数据存在的可能性。所以如果通过BitSet的布隆表达式查询该Key存在时，只是一个理论存在可能，接下来要通过IndexBlock真正进行查询。而如果布隆表达式在BitSet中没有找到，那就是真的没有，可以快速跳过，进入下一个SSTable查找。布隆表达式的运用，能够大大提高查找效率。

5.6 如何进行数据的删除和更新

为了保证数据的顺序写，所有SSTable都不会因为删除和更新而在原数据所在位置进行更改。在更新时，仅仅插入一个最新的值去写到新的SSTable中。在删除时，依然是插入一个基于该Key的删除标记，写入最新的SSTable中。由于查找某个Key是基于时间新鲜度，反向依次查找SSTable，所以读取某个Key始终读的是最新的值。

5.7 SSTable的合并

随着日积月累，SSTable的文件数会增多，导致查找时性能下降。同时由于数据的更新或删除。让老的SSTable中数据的有效性降低，太多的过期数据占用SSTable，同样会降低查询效率。所以一般数据库引擎，定期都会有一个SSTable的合并操作。移除过时数据，将多个小SSTable合并成大的SSTable。

5.8 最近读取的SSTable IndexBlock缓存

在大内存的条件下，部分数据库还会将最近读取的SSTable　索引，缓存至内存。这进一步加速了查找的过程。

六、参考文献

http://www.benstopford.com/2015/02/14/log-structured-merge-trees/

http://www.cnblogs.com/haippy/archive/2011/12/04/2276064.html

https://blog.csdn.net/u014774781/article/details/52105708

https://en.wikipedia.org/wiki/Log-structured_merge-tree

https://www.igvita.com/2012/02/06/sstable-and-log-structured-storage-leveldb/

欢迎关注我的个人公众号"西北偏北UP"，记录代码人生，行业思考，科技评论