[JSOI2019]节日庆典 做题心得

[JSOI2019]节日庆典 做题心得

一个性质有趣的字符串题

这要是在考场上我肯定做不出来吧

一开始还以为要 SAM 什么的暴力搞，没想到只用到了 \(Z\) 函数 —— 也是我生疏了罢

（学了啥忘了啥，这可怎么去wc啊啊啊

思路

考虑维护候选集合 \(S\)，表示这个位置 可能 是最优位置。

假设我们可以知道 \(S\)，拿 \(Z\) 函数求一下 \(LCP\) 就可以知道是不是最优的了。

大胆猜测一个性质，要么可以快速的找 \(S\) 中最小的位置，要么 \(S\) 的大小不会很大，可以暴力找。

第一个思路不太好搞，那看来就选第二个思路吧

假设现在考虑前 \(k\) 位

首先可以来一个优化：如果还没循环，就比出来了胜负，那么大的那个一定不会是最优解 —— 并且随着 \(k\) 的增加，显然不会翻身成更优的

那现在对于 \(i,j\in S,i<j\)，一定有 \(LCP(s[i:k],s[j:k])= k-j+1\)。

考虑两个 \(i,j\) ，如果 \([i,i+LCP-1]\) 和 \([j,j+LCP-1]\) 不重合，看来没什么性质

如果重合，似乎有些有趣的性质，先放结论：

如果重合，即 \(k-j+1>j-i\)，则 \(j\) 一定不会是最优的

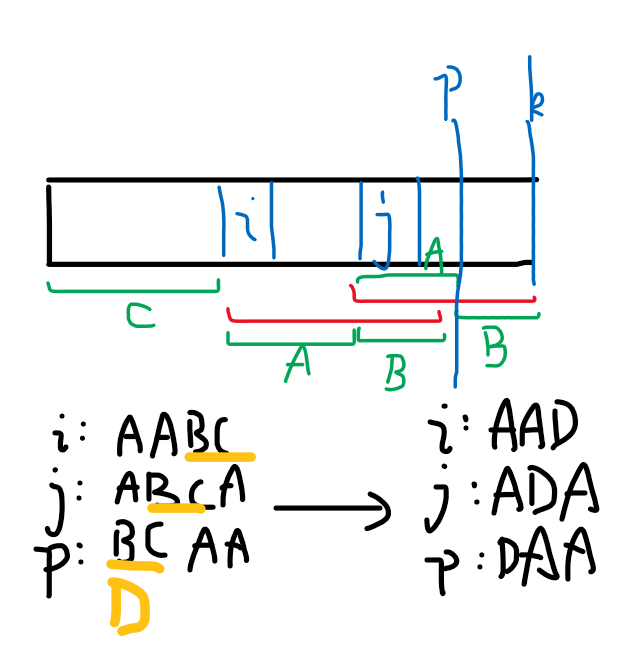
我相信这个图还挺清楚的

红色是 \(i,j\) 的 \(LCP\)。然后设 \(i\) 到 \(j\) 前面是 \(A=s[i:j-1]\)，然后红色减去 \(A\) 之后剩下的是 \(B=s[j:i+LCP-1]\)，是从 \(j\) 开始的。由于两个红色相等，所以 \(B\) 是红色的前缀，对应到后面，它也是红色的后缀（即它是红色的 border）

\(p\) 是 \(j\) 往后数一个 \(A\) 之后的开始位置

设 \(i\) 前面的是 \(C\)。\(i\) 开始的循环串就是 \(AABC\)，\(j,p\) 同理

然后发现 \(BC\) 作为一个整体出现，把它看成 \(D\)。然后就清楚多了：

如果 \(D<A\)，那么 \(p\) 开始是最小的；

如果 \(A<D\)，那么 \(i\) 开始是最小的；

如果 \(A=D\)，那么三个一样大；

总之，忽略 \(j\) ，对最大值没有影响

那么 \(S\) 集合中，每往前数一个数，它到上一个的距离，都比上一个到 \(k\) 的距离大。和启发式合并类似的，有一个基本事实：

一个数加上比它大的数，至少翻一倍

那 \(S\) 集合中数到 \(k\) 的距离，每次至少翻一倍，所以 \(S\) 的大小是 \(\log\) 的。

每次新加入元素的时候维护一下即可，然后分段考虑一下，求最小的那个开始位置。

#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
	#define N 10000007
	#define F(i,l,r) for(int i=l;i<=r;++i)
	#define D(i,r,l) for(int i=r;i>=l;--i)
	#define Fs(i,l,r,c) for(int i=l;i<=r;c)
	#define Ds(i,r,l,c) for(int i=r;i>=l;c)
	#define MEM(x,a) memset(x,a,sizeof(x))
	#define FK(x) MEM(x,0)
	#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
	#define p_b push_back
	#define sz(a) ((int)a.size())
	#define all(a) a.begin(),a.end()
	#define iter(a,p) (a.begin()+p)

	int n;
	char s[N];
    void Input()
    {
    	scanf("%s",s+1);
    	n=strlen(s+1);
    }
	int z[N];
	void Z_Function()
	{
		z[1]=n; F(i,2,n) z[i]=0;
		int l=0,r=0;
		F(i,2,n)
		{
			if (i<=r) z[i]=min(z[i-l+1],r-i+1);
			while(i+z[i]<=n and s[i+z[i]]==s[z[i]+1]) ++z[i];
			if (i+z[i]-1>=r) l=i,r=i+z[i]-1;
		}
	}
	int c[N],cp=0;
	int stk[N],top=0;
	void fuckoff(int k)
	{
		while(top) stk[top--]=0;
		F(i,1,cp)
		{
			int x=c[i];
			while(top and s[stk[top]+k-x]>s[k])
			{
				--top;
			}
			if (top and s[stk[top]+k-x]<s[k]) continue;
			stk[++top]=x;
		}
		F(i,1,cp) c[i]=0; cp=top; F(i,1,top) c[i]=stk[i];

		while(top) stk[top--]=0;
		D(i,cp,1)
		{
			while(top and k-stk[top]+1>stk[top]-c[i]) --top;
			stk[++top]=c[i];
		}
		F(i,1,cp) c[i]=0; cp=top; F(i,1,top) c[i]=stk[top-i+1];
	}
	int getmin(int k)
	{
		int ansp=c[1];
		F(i,2,cp)
		{
			int x=c[i];
			// printf("x=%d cur=%d\n",x,ansp);
			int LCP1=k-x+1;
			int LCP2=min(z[ansp+LCP1],k-(ansp+LCP1)+1);
			// printf(" LCP2=%d\n",LCP2);
			if (LCP2<k-(ansp+LCP1)+1)
			{
				int p1=ansp+LCP1+LCP2;
				int p2=LCP2+1;
				// printf(" case2 p1=%d p2=%d\n",p1,p2);
				if (p2>k) continue;
				if (s[p1]>s[p2])
				{
					// puts(" better");
					ansp=x;
				}
			}
			else
			{
				int LCP3=min(z[LCP2+1],k-LCP2);
				int p1=LCP3+1;
				int p2=LCP2+LCP3+1;
				// printf(" LCP3=%d\n",LCP3);
				// printf(" case3 p1=%d p2=%d\n",p1,p2);
				if (p2>k) continue;
				if (s[p1]>s[p2])
				{
					// puts(" better");
					ansp=x;
				}
			}
		}
		return ansp;
	}
    void Sakuya()
    {
    	Z_Function();
    	F(i,1,n)
    	{
    		c[++cp]=i;
    		fuckoff(i);
    		printf("%d ",getmin(i));
    	}
    	puts("");
    }
    void IsMyWife()
    {
        Input();
        Sakuya();
    }
}
#undef int //long long
int main()
{
    Flandre_Scarlet::IsMyWife();
    getchar();
    return 0;
}