【Notes_3】现代图形学入门——基础变换、MVP变换模型

基础变换(二维)

三维变化与二维变换矩阵类似

齐次坐标下的基础变换

Scale:

\[S(s_x,s_y) =\begin{pmatrix}
s_x &0 &0\\
0 & s_y & 0 \\
0&0&1
\end{pmatrix}\]

Rotation:

\[R(\alpha) = \begin{pmatrix}
\cos\alpha& - \sin\alpha & 0 \\
\sin\alpha & \cos \alpha &0 \\
0&0&1
\end{pmatrix}\]

Translation:

\[T(t_x,t_y)=\begin{pmatrix}
1 & 0 & t_x \\
0 &1& t_y\\
0 &0& 1
\end{pmatrix}\]

组合变换(Compositon Transform)

矩阵变换把先变化的矩阵放到右边：矩阵运算是从右向左

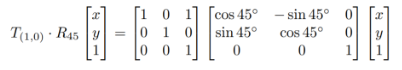
四元数与旋转公式

四元数

留个坑，下周再填

罗德里格斯旋转公式

Rodrigue's Rotation Formula: Raotation by angle \(\alpha\) around axis \(\vec{n}\)

\[R(\vec{n},\alpha)=cos(\alpha)I+(1-cos(\alpha))nn^{T}+\sin(\alpha)
\begin{matrix} \underbrace{
\begin{pmatrix}
0 & -n_z & n_y \\
n_z & 0 & -n_x \\
-n_y & n_x & 0
\end{pmatrix}
} \\ N\end{matrix}\]

In the formula

I ：Identity matrix

最后乘积的结果是一个3*3的矩阵

MVP变换

Model Transformation

引用博客：MVP变换

对模型进行模型变换时，需要注意坐标系是在世界坐标系原点。当绕模型中心进行变换时，首先要将模型的中心点移动到世界坐标系的原点，之后在进行模型变换，之后移回到原来的位置。

矩阵描述为：$$M=M_t^{-1} M_r M_s M_t$$

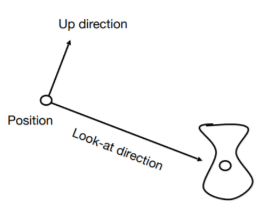
View/Camera Transformation

这个过程是将确定相机的位置：将相机的位置通过下面的过程移动到固定的点和方向。

(1) 相机的位置固定在世界坐标系的原点： \(\vec{e}\)

(2) 相机的朝向 \(-\vec{Z}\)： \(\hat{g}\)

(3) 相机的向上方向\(\vec Y\)： \(\hat t\)

基于上述过程，要求视图变换矩阵\(M_{view}\)分别求相机的平移矩阵\(T_{view}\)、旋转矩阵\(R_{view}\)

\[T_{view} = \begin{bmatrix}
1 & 0 & 0 & -x_{\vec{e}} \\
0 & 1 & 0 & -y_{\vec{e}} \\
0 & 0 & 1 & -z_{\vec{e}} \\
0 & 0 & 0 & 1
\end{bmatrix}\]

求旋转矩阵时，直接求相机旋转到原点的矩阵不容易求解，但求原点到相机位置的旋转矩阵容易求。

所以先求原点到相机的旋转矩阵：Z To \(-\hat{g}\)、Y To \(\hat{t}\)、最后保证\(\vec{X}\) To \((\hat g \times \hat t)\) 朝向的方向，原因是保证符合右手坐标系。

\[R_{view}^{-1}=\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&x_{t}&x_{-g}&0\\
y_{\hat{g} \times \hat{t}}&x_{t}&y_{-g}&0\\
z_{\hat{g} \times \hat{t}}&x_{t}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}\]

因为\(R_{view}^{-1}\)是正交矩阵，所以逆矩阵和旋转矩阵相同。

\[R_{view} =\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\
x_{t}&y_{t}&z_{t}&0\\
x_{-g}&y_{-g}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}\]

所以

\[M_{view} = R_{view} T_{view}=
\begin{bmatrix}
x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\
x_{t}&y_{t}&z_{t}&0\\
x_{-g}&y_{-g}&z_{-g}&0\\
0&0&0&1
\end{bmatrix}
\]

\[\begin{bmatrix}
1 & 0 & 0 & -x_{\vec{e}} \\
0 & 1 & 0 & -y_{\vec{e}} \\
0 & 0 & 1 & -z_{\vec{e}} \\
0 & 0 & 0 & 1
\end{bmatrix}\]

Projection Transformation

个人理解投影变换的终极目的是让物体挤压在一个单位大小的平面(空间)内。原因先挖个坑。

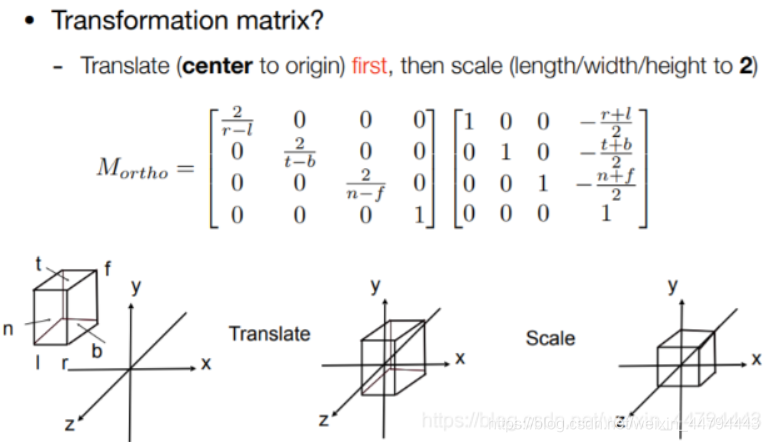
Orthographic Projection

简单理解就是将物体的忽略z坐标，将模型通过Scale To [-1,-1]^2平面内。

真正的操作：

(1) 移动模型的位置到原点

(2) 缩放模型到空间[-1,1]^3中

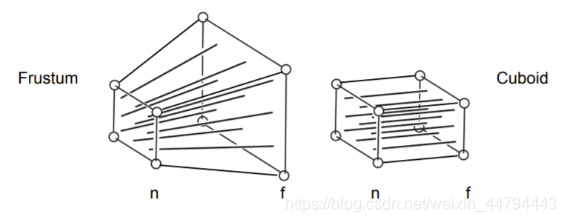
Perspective Projection

正视投影的光线可以看成是一个立方体，如上图。透视投影的光线可以看成一个视锥，如下图。

透视变换可以分为两个步骤进行：

(1) 将视锥挤压到立方体内\(M_{persp->ortho}\)

(2) 将挤压后的视锥进行正视投影变换$M_{ortho}

挤压时的变换矩阵\(M_{persp->ortho}=\begin{bmatrix}
n&0&0&0\\
0&n&0&0\\
0&0&n+f&-nf\\
0 & 0&1&0
\end{bmatrix}\)

所以投影变换矩阵

\[M_{proj}=M_{ortho}M_{persp->ortho}
\]