C++算法 线段树

线段树这个算法，看起来非常高端，而且很有用处，所以还是讲一下下吧。

温馨提示：写线段树前请做好写码5分钟，调试一辈子的准备^-^

啊直接步入正题……

首先我们考虑一个题目：有一个序列，要做到单点修改单点查询，该怎么做呢？

同学们先不要着急关掉……我们细细分析，像这种题，明显大家都知道……直接暴力就过了嘛……，所以不做分析……

然后我们考虑第二个题目：有一个序列，要做到单点修改区间求和，该怎么做呢？

像传统的for(int i=1;i<=n;i++)ans+=a[i]当然是很香的，但如果遇到一些非常奇怪的题目（数 据 大 到 你 自 闭），这个就没什么用了……

啊这，简单的暴力不能用，就要用复杂的暴力——线段树，当然是简单亿点点的~因为单点修改可以O(1)，不存在浪费时间的事情，所以我们用线段树小小的处理一下就好了。

接下来画一个图帮助斯烤：

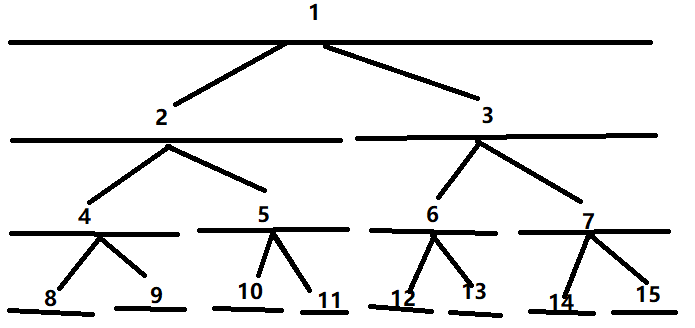
在这个图上呢……一共有8个点，就是底下那些最小的线段，而我们把他合成了许多部分，每个部分的值就是f[wz*2]+f[wz*2+1]（f是每个的值，wz是每个的编号)。

然后就可以把他一直向下，一直向下，直到发现这个区间是被我们要求的区间所包含的，然后这个区间内的数就全部加上，就这么一直向下找找找……，最后就可以算出一个区间的总和。

下面是演示代码~

void qh(long long wz)//wz是现在所处的小块编号
{
	if(tree[wz].l>=a&&tree[wz].r<=b)//a和b是我们要求的区间的左右端点
	{
		zshu+=tree[wz].shu;//全部被包含，直接加上
		return;
	}
	long long mid=(tree[wz].l+tree[wz].r)/2;//不能被包含?分裂一下试试吧
	if(b>mid)//和谐小细节~
	{
		qh(wz*2+1);//如果有被包含，就去右边的小块看看
	}
	if(a<=mid)//和谐小细节*2~(至于为啥有和谐小细节，以及为什么要这样写，请同学们自己斯烤(这么简单还是可以的8))
	{
		qh(wz*2);//如果有被包含，也要去左边的小块看看
	}
}

嘿嘿简单吧^-^，啊我忘记讲建树了QAQ。没事马上就讲。

建树嘛，直接递归就好了，每次把这个区间分成两份，一直分到l和r一样（就是说这是一个点的值，要输入了），然后获取两个点的值之后就可以向上递归~嗯嗯对，一直递归就建好了，相信大家都有这个写递归的能力，但要实在不会就看看下面的代码吧（温馨提示：线段树用来建树的数组要开到节点数的4倍大，至于为什么我也忘了……）：

struct hehe
{
	long long l,r,shu,f;
}tree[400005];//tree结构体~
long long mid;
void js(long long ll,long long rr,long long wz)//js，建树的意思。ll和rr分别是左右边界，wz就是他的编号
{
	tree[wz].l=ll;//左边界是ll
	tree[wz].r=rr;//右边界是rr
	if(ll==rr)//左右边界一致，这是一个点
	{
		scanf("%lld",&tree[wz].shu);
		return;
	}
	long long mid=(ll+rr)/2;//如果这不是一个点，肯定能分成两部分
	js(ll,mid,wz*2);//左边
	js(mid+1,rr,wz*2+1);//右边
	tree[wz].shu=tree[wz*2].shu+tree[wz*2+1].shu;//加起来
}

看，是不是非常简单，接下来为了学的更深一点点，要把题目加难了（是的还要加难，但我相信你们一定可以学会的）

有一个序列，要做到区间增加区间求和，该怎么做呢？

啊这，这个是线段树里最难的一部分（起码我觉得最难），直接下放显然不太现实……，会浪费掉很多不必要的时间。正所谓科技发展在于懒人~，其实我们也可以在不影响结果的情况下偷个懒是吧QWQ。

就像加一样~我知道这两个序列的和，我就没必要去求所有单个序列是多少，加法和这个差不多，我们可以看看有那个序列是全都要加的，然后直接算出它加完之后的值。这样求这个值的时候肯定是不影响计算的（偷懒成功！）。但这时就会有一些同学吐槽："啊你这个不严谨啊，如果下一次求和是求这个序列的一部分怎么办呢？"其实呢，我刚才也写了是吧……

其实我们也可以在不影响结果的情况下偷个懒是吧

我刚才说的是不影响，但这个操作明显影响了，在哪里影响了呢？就是只加了一个总序列，没有让他的一部分加上（偷懒失败QWQ）。但好像根本没有必要调整他的一部分啊，因为目前根本用不到，没说让做的事情我们还要去做不是浪费时间吗？但又不能不加，怎么办呢？我们可以设定一个懒标记，表示它之前被加了多少，这样呢，每次要求和的时候只要下放这个懒标记，并且加上该加的数，就能达到不说不做，最大程度优化时间，还保证正确hhhhh（偷懒成功）

至于代码的实现也是非常的简单：

void xf(long long wz)
{
	tree[wz*2].shu+=(tree[wz*2].r-tree[wz*2].l+1)*tree[wz].f;//每个长度单位都加上tree[wz].f，总值就增加了(tree[wz*2].r-tree[wz*2].l+1)*tree[wz].f
	tree[wz*2].f+=tree[wz].f;//之前每一个长度单位要加tree[wz*2].f，现在发现它还要加上tree[wz].f，就把他们两个加起来就好了嘛，很容易的。
	tree[wz*2+1].shu+=(tree[wz*2+1].r-tree[wz*2+1].l+1)*tree[wz].f;
	tree[wz*2+1].f+=tree[wz].f;//同理
	tree[wz].f=0;//这里已经加过了，要清零的，就像转账一样，你给另一个人转了钱，你钱就没了。
}

上方是下放懒标记的代码，下方是区间修改代码：

void xg(long long wz)
{
	if(tree[wz].l>=a&&tree[wz].r<=b)
	{
		tree[wz].shu+=(tree[wz].r-tree[wz].l+1)*c;//更改值
		tree[wz].f+=c;//增加懒标记
		return;
	}//啊后面的都说过，不打了…
	tree[wz].shu+=(min(tree[wz].r,b)-max(tree[wz].l,a)+1)*c;
	long long mid=(tree[wz].l+tree[wz].r)/2;
	if(b>mid)
	{
		xg(wz*2+1);
	}
	if(a<=mid)
	{
		xg(wz*2);
	}
}

至于加了懒标记以后别的代码也是要动的。

比如在原来的求和代码里多了一个xf(wz);

至于加在哪里同学们自己斯烤吧（我太仁慈了）

啊我再放一道线段树模板题，大家可以秒掉来吊打我：模板题传送们

好了我觉得我讲完了，如果有什么不好或漏掉的地方大家可以及时评论，我会更改的。