Java 树结构实际应用 三（二叉排序树）

二叉排序树

1 先看一个需求

给你一个数列 (7, 3, 10, 12, 5, 1, 9)，要求能够高效的完成对数据的查询和添加

 

2 解决方案分析

 使用数组

数组未排序， 优点：直接在数组尾添加，速度快。 缺点：查找速度慢. 

数组排序，优点：可以使用二分查找，查找速度快，缺点：为了保证数组有序，在添加新数据时，找到插入位

置后，后面的数据需整体移动，速度慢。

 使用链式存储-链表

不管链表是否有序，查找速度都慢，添加数据速度比数组快，不需要数据整体移动。

 使用二叉排序树

 

3 二叉排序树介绍

　　二叉排序树：BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当

前节点的值小，右子节点的值比当前节点的值大。

　　特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点

　　比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ，对应的二叉排序树为：

4 二叉排序树创建和遍历

一个数组创建成对应的二叉排序树，并使用中序遍历二叉排序树，比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) ， 创

建成对应的二叉排序树为 : 

5 二叉排序树的删除

二叉排序树的删除情况比较复杂，有下面三种情况需要考虑

1) 删除叶子节点 (比如：2, 5, 9, 12)

2) 删除只有一颗子树的节点 (比如：1)

3) 删除有两颗子树的节点. (比如：7, 3，10 )

4) 操作的思路分析

对删除结点的各种情况的思路分析:

第一种情况:

删除叶子节点 (比如：2, 5, 9, 12)

思路

(1) 需求先去找到要删除的结点 targetNode

(2) 找到 targetNode 的 父结点 parent

(3) 确定 targetNode 是 parent 的左子结点 还是右子结点

(4) 根据前面的情况来对应删除

左子结点 parent.left = null

右子结点 parent.right = null;

第二种情况: 删除只有一颗子树的节点 比如 1

思路

(1) 需求先去找到要删除的结点 targetNode

(2) 找到 targetNode 的 父结点 parent

(3) 确定 targetNode 的子结点是左子结点还是右子结点

(4) targetNode 是 parent 的左子结点还是右子结点

(5) 如果 targetNode 有左子结点

(5). 1 如果 targetNode 是 parent 的左子结点

parent.left = targetNode.left;

(5).2 如果 targetNode 是 parent 的右子结点

parent.right = targetNode.left;

(6) 如果 targetNode 有右子结点

(6).1 如果 targetNode 是 parent 的左子结点

parent.left = targetNode.right;

(6).2 如果 targetNode 是 parent 的右子结点

parent.right = targetNode.righ

情况三 ： 删除有两颗子树的节点. (比如：7, 3，10 )

思路

(1) 需求先去找到要删除的结点 targetNode

(2) 找到 targetNode 的 父结点 parent

(3) 从 targetNode 的右子树找到最小的结点

(4) 用一个临时变量，将 最小结点的值保存 temp = 11

(5) 删除该最小结点

(6) targetNode.value = temp

 

6 二叉排序树删除结点的代码实现

package com.lin.binarysorttree_0314;

public class BinarySortTreeTest {

    public static void main(String[] args) {
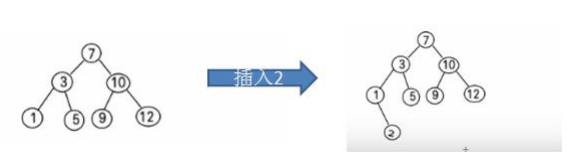
        int[] arr = {7, 3, 10, 12, 5, 1, 9};
        BinarySortTree binarySortTree = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            binarySortTree.add(new SNode(arr[i]));
        }

        binarySortTree.add(new SNode(2));
        binarySortTree.infixOrder();

        // 删除
        System.out.println("***********");

        binarySortTree.delNode(2);
        binarySortTree.delNode(3);
        binarySortTree.delNode(5);
        binarySortTree.delNode(7);
        binarySortTree.delNode(9);
        binarySortTree.delNode(12);
        System.out.println("root:" + binarySortTree.getRoot());

        binarySortTree.infixOrder();
    }
}

class BinarySortTree{
    private SNode root;
    // 查找要删除的节点
    public SNode getRoot() {
        return root;
    }
    public SNode searchDelNode(int value) {
        if(root == null) {
            return null;
        } else {
            return root.searchDelNode(value);
        }
    }
    // 查找要删除节点的父节点
    public SNode searchParent(int value) {
        if(root == null) {
            return null;
        } else {
            return root.searchParent(value);
        }
    }
    /**
     * @param node 传入的节点（当作二叉排序树的根节点）
     * @return 返回的以node为根节点的二叉排序树的最小节点的值
     */
    public int delRightTreeMin(SNode node) {
        SNode target = node;
        //    循环地查找左节点，就会找到最小值
        while(target.left != null) {
            target = target.left;
        }
        delNode(target.value);// !!!!
        return target.value;//   !!!!!
    }

    // 删除节点
    public void delNode(int value) {
        if(root == null) {
            return;
        } else {
            //     找删除节点
            SNode targetNode = searchDelNode(value);
            //     没有找到
            if(targetNode == null) {
                return;
            }
            //    如果发现当前这棵二叉树只有一个节点
            if(root.left == null && root.right == null) {
                root = null;
                return;
            }
            //     去找到targetNode的父节点
            SNode parent = searchParent(value);
            //     如果删除的节点是叶子节点
            if(targetNode.left == null && targetNode.right == null) {
                //    判断targetNode是父节点的左子节点还是右子节点
                if(parent.left != null && parent.left.value == value) {
                    parent.left = null;
                } else if(parent.right != null && parent.right.value == value) {
                    parent.right = null;
                }
            } else if(targetNode.left != null && targetNode.right != null) { //    有左右子节点
                int delRightTreeMin = delRightTreeMin(targetNode.right);
                targetNode.value = delRightTreeMin;
            } else {//    只有一个子节点
                //     要删除的节点只有左节点
                if(targetNode.left !=  null) {
                    if(parent != null) {
                        //     如果targetNode是parent的左子节点
                        if(parent.left.value == value) {
                            parent.left = targetNode.left;
                        } else {
                            parent.right = targetNode.left;
                        }
                    } else {
                        root = targetNode.left;
                    }
                } else {//    要删除的节点有右子节点
                    if(parent != null) {
                        if(parent.left.value == value) {
                            parent.left = targetNode.right;
                        } else {
                            parent.right = targetNode.right;
                        }
                    } else {
                        root = targetNode.right;
                    }
                }
            }

        }
    }
    // 中序遍历
    public void infixOrder() {
        if(root == null) {
            System.out.println("空树！");
        } else {
            root.infixOrder();
        }
    }
    // 添加
    public void add(SNode node) {
        if(root == null) {
            root = node;
        } else {
            root.add(node);
        }
    }
}

class SNode{
    protected int value;
    protected SNode left;
    protected SNode right;

    public SNode(int value) {
        // TODO Auto-generated constructor stub
        this.value = value;
    }

    @Override
    public String toString() {
        // TODO Auto-generated method stub
        return "Node = [value = " + value + "]";
    }

    // 添加节点
    public void add(SNode node) {
        if(node == null) {
            return;
        }
        if(node.value < this.value) {
            if(this.left == null) {
                this.left = node;
            } else {
                this.left.add(node);
            }
        } else {
            if(this.right == null) {
                this.right = node;
            } else {
                this.right.add(node);
            }
        }
    }
    // 中序遍历
    public void infixOrder() {
        if(this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right != null) {
            this.right.infixOrder();
        }
    }
    // 查找要删除的节点
    public SNode searchDelNode(int value) {
        if(this.value == value) {
            return this;
        } else if(this.value > value) {
            // 如果左子节点为空
            if(this.left == null) {
                return null;
            }
            return this.left.searchDelNode(value);
        } else {
            if(this.right == null) {
                return null;
            }
            return this.right.searchDelNode(value);
        }
    }
    // 查找要删除节点的父节点, 如果没有则返回null
    public SNode searchParent(int value) {
        if(( this.left != null && this.left.value == value)
                || ( this.right != null && this.right.value == value )) {
            return this;
        } else {
             // 如果查找的值小于当前节点的值，并且当前节点的左子节点不为空
            if(value < this.value && this.left != null) {
                return this.left.searchParent(value);
            } else if(value >= this.value && this.right != null) {
                return this.right.searchParent(value);
            } else {
                return null;
            }
        }
    }

}

仅供参考，有错误还请指出！

有什么想法，评论区留言，互相指教指教。

觉得不错的可以点一下右边的推荐哟