BZOJ1294 洛谷P2566 状态压缩DP 围豆豆

传送门

题目描述

是不是平时在手机里玩吃豆豆游戏玩腻了呢？最近MOKIA手机上推出了一种新的围豆豆游戏，大家一起来试一试吧游戏的规则非常简单，在一个N×M的矩阵方格内分布着D颗豆子，每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格，每次移动可以随意的走到相邻的四个格子，直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物，任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0，即什么都不注意路径包围的概念，即某一颗豆在路径所形成的多边形（可能是含自交的复杂多边形）的内部。下面有两个例子：

第一个例子中，豆在路径围成的矩形内部，所以豆被围住了。第二个例子中，虽然路径经过了豆的周围的8个格子，但是路径形成的多边形内部并不包含豆，所以没有围住豆子。

布布最近迷上了这款游戏，但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。

输入格式

第一行两个整数N和M，为矩阵的边长。

第二行一个整数D，为豆子的总个数。

第三行包含D个整数V1到VD，分别为每颗豆子的分值。

接着N行有一个N×M的字符矩阵来描述游戏矩阵状态，0表示空格，#表示障碍物。而数字1到9分别表示对应编号的豆子。

输出格式

仅包含一个整数，为最高可能获得的分值。

输入输出样例

样例输入

 - 

#

样例输出

38

说明/提示

50%的数据满足1≤D≤3。

100%的数据满足1≤D≤9，1≤N, M≤10，-10000≤Vi≤10000。

分析

一看到是方格中的问题，数据范围又在10以下，显然是状态压缩DP了

这道题的细节比较多，而且用到了位运算，所以有些代码不太好理解，因此我感觉分块讲会比较好理解

问题一、数组的定义

如果你要进行动态规划，肯定要开一个数组存储存储结果

这道题开二维数组显然是不够用的，因为我们既要记录一个点的横坐标，又要记录一个点的纵坐标

我们设f[x][y][s]为走到坐标为（x,y）的点，且状态为S时所走过的路程长度

x,y的含义大家应该很容易就可以理解，关键是状态S

我们可以这样想在方格中最多有9个豆豆，所以我们可以用一个长度为9的二进制数来存储状态

什么意思呢？我们还是来举一个例子

比如说方格中有4个豆子，那么

0 0 0 0 表示你一个豆子也没有围上

0 0 1 0 表示你把第二个豆子围上

0 1 1 1 表示你把第1、2、3个豆子全部围上

这样的话大家应该就可以理解了

这里还需要注意的是，因为我们每一次开始遍历的起点不同，所以最终得到的答案也不同，因此我们每选择一个起点，就要重新将f数组初始化

问题二、围住的判断

只有某一颗豆在路径所形成的多边形（可能是含自交的复杂多边形）的内部时，我们才可以得到这个豆子的价值

我们来举几个例子

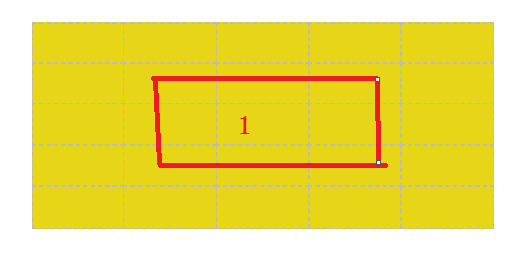
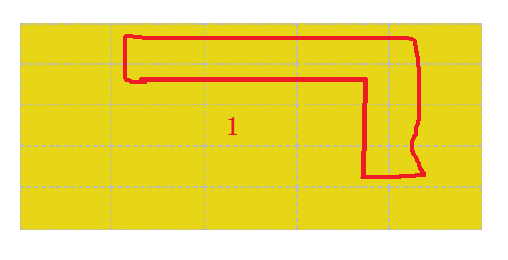
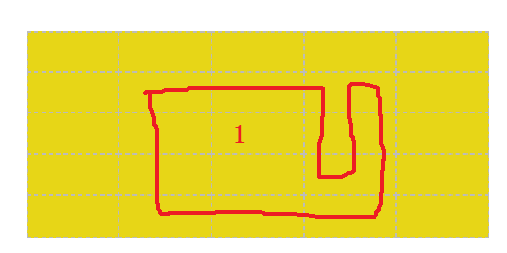
我们可以看到，左边的这两幅图中豆豆是可以被围住的，而右边的这两幅图中，豆豆是无法被围住的

那么它们分别有什么特点呢？

我们从豆豆开始向右引一条射线（其实向哪一个方向都可以），如果射线与路径的交点为奇数个，那么豆豆能被围住，反之则不能

（这其实就是射线定理，大家有兴趣的话可以百度一下证明）

这样的话，我们只要判断路径与射线的交点个数是不是就可以了呢

其实还是不行，比如下面这幅图

射线与路径的交点有三个（绿色的圈圈住的部分），但是豆豆没有被包含在里面

所以只有当上下移动时，我们才可以给路径计数，如果是左右水平移动的话，我们就不能算进去

这是对于上下移动的判断，mx、my分别是移动之前点的横纵坐标，nx、ny分别是移动之后点的横纵坐标

ax数组记录的是所有豆豆的横坐标，ay数组记录的是所有豆豆的纵坐标

前面的四个判断是对于上下移动的判断，只有上下移动才可以计数

最后一个判断是判断该路径是否在豆豆的右边（因为我是向右引的射线）

当然你把里面的==都改成>=也可以，但是没有必要，因为你一次只能走一个格子

问题三、怎么由上一个格子的状态ms推出下一个格子的状态ns

先上代码

int solve(int mx,int my,int nx,int ny,int ms){
    int ns=ms;
    for(int i=;i<=d;i++){
        if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){
            ns^=(<<(i-));
        }
    }
    return ns;
}

mx、my分别是移动之前点的横纵坐标，nx、ny分别是移动之后点的横纵坐标

ms是上一个格子的状态，ns是下一个格子的状态（什么是状态我们在第一个问题中已经提到过了）

ax数组记录的是所有豆豆的横坐标，ay数组记录的是所有豆豆的纵坐标

在第三行我们枚举每一个豆豆，在第四行我们判断当前移动能否计数（问题二中已经说过）

最关键的就是第五行  ns^=(1<<(i-1))

这是什么意思呢，我们可以这样考虑

ns必定要由ms推导出来，我们枚举每一个豆豆，如果当前走的路径可以与射线相交，那么必定会改变交点个数的奇偶性

也就是说，豆豆本来在四边形内，走了这一步，就到了四边形外；或者豆豆本来在四边形外，走了这一步，就到了四边形内

我们知道状态S如果从右往左数第i位为1，则说明第i个豆豆在格子内，反之亦然

那么如果从右往左数第i位状态变化了，我们只需要将当前的状态和（1<<(i-1)）取异或，就相当于把第i为取反，其他位不变

这样就达到了我们的目的

（我感觉已经讲得很清楚了，如果再不理解，我也没有办法了）

问题四、通过什么来算出f数组呢

我们可以用SPFA，也可以用bfs

不同的是bfs每个元素只会进栈一次，而SPFA可以进很多次

但是实际上你即使用SPFA每个点也只会松弛一次，因为你的路径只会越走越长用bfs和用SPFA没什么区别

但是要注意vis数组的初始化，用bfs的话vis数组必须初始化，但是用SPFA则不用

因为SPFAvis数组最后的状态必定为0

最终的状态转移方程为：ans=max(ans,val[i]-f[ii][jj][i])

val[i]是我们预处理出来的状态为i时豆子的总价值，预处理过程如下:

    for(int i=;i<mmax;i++){
        for(int j=;j<=d;j++){
            if(i&(<<(j-))) val[i]+=da[j];
        }
    }

da[j]是第j个豆子的价值，ans使我们最终要的结果

豆子的总价值减去路程上的花费得出来的结果，最后再取一个最大值显然是我们想要的ans

代码（前面该说的都说了，注释我就少加点）

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cstring>
 using namespace std;
 int n,m,d;
 int mmax,f[][][<<],da[],val[<<];
 struct asd{
     int x,y,s;
     asd(int aa=,int bb=,int cc=){
         x=aa,y=bb,s=cc;
     }
 };//跑bfs的结构体
 char c[][];
 int xx[]={,-,,},yy[]={-,,,},ax[],ay[];
 //xx,yy枚举走的方向，ax,ay记录豆豆的横纵坐标
 int ans=-0x3f3f3f3f;//记录最终价值
 int vis[][][<<];//判断该点是否已经遍历过
 int solve(int mx,int my,int nx,int ny,int ms){
     int ns=ms;
     for(int i=;i<=d;i++){
         if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){
             ns^=(<<(i-));
         }
     }
     return ns;
 }
 void bfs(int ii,int jj){
     queue<asd> q;
     q.push(asd(ii,jj,));
     memset(f,0x3f,sizeof(f));
     memset(vis,,sizeof(vis));
     f[ii][jj][]=;
     while(!q.empty()){
         asd aa=q.front();
         q.pop();
         int mx=aa.x,my=aa.y,ms=aa.s;
         vis[mx][my][ms]=;
         for(int i=;i<;i++){
             int nx=mx+xx[i],ny=my+yy[i];
             if(nx< || ny< || nx>n || ny>m || (c[nx][ny]>='' && c[nx][ny]<='') || c[nx][ny]=='#') continue;
              //判断该点是否能走
             //注意豆豆所在的方格也不能走
             int ns=ms;
             if(i&) ns=solve(mx,my,nx,ny,ms);
             //只有在上下走的时候才改变状态，否则状态不变
             //如果不能理解也可以写成i==1 || i==3
             if(vis[nx][ny][ns]==) continue;
             //如果已经更新过，就不再更新
             if(f[mx][my][ms]<f[nx][ny][ns]){
                 f[nx][ny][ns]=f[mx][my][ms]+;
                 vis[nx][ny][ns]=;
                 q.push(asd(nx,ny,ns));
             }
         }
     }
     for(int i=;i<mmax;i++){
         ans=max(ans,val[i]-f[ii][jj][i]);
     }
 }
 int main(){
     scanf("%d%d%d",&n,&m,&d);
     for(int i=;i<=d;i++){
         scanf("%d",&da[i]);
     }
     mmax=<<d;
     for(int i=;i<mmax;i++){
         for(int j=;j<=d;j++){
             if(i&(<<(j-))) val[i]+=da[j];
         }
     }
     for(int i=;i<=n;i++){
         scanf("%s",c[i]+);
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]>'' && c[i][j]<=''){
                 int now=c[i][j]-'';
                 ax[now]=i,ay[now]=j;
             }
         }
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]==''){
                 bfs(i,j);
                 //如果该点为0，就可以作为起点
             }
         }
     }
     printf("%d\n",ans);
     return ;
 }

bfs

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cstring>
 using namespace std;
 int n,m,d;
 int mmax,f[][][<<],da[],val[<<];
 struct asd{
     int x,y,s;
     asd(int aa=,int bb=,int cc=){
         x=aa,y=bb,s=cc;
     }
 }b[*];
 char c[][];
 int xx[]={,-,,},yy[]={-,,,},ax[],ay[];
 int ans=-0x3f3f3f3f;
 int vis[][][<<];
 inline int solve(int mx,int my,int nx,int ny,int ms){
     int ns=ms;
     for(int i=;i<=d;i++){
         if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){
             ns^=(<<(i-));
         }
     }
     return ns;
 }
 inline void SPFA(int ii,int jj){
     queue<asd> q;
     q.push(asd(ii,jj,));
     memset(f,0x3f,sizeof(f));
     f[ii][jj][]=;
     //memset(vis,0,sizeof(vis));
     while(!q.empty()){
         asd aa=q.front();
         q.pop();
         int mx=aa.x,my=aa.y,ms=aa.s;
         vis[mx][my][ms]=;
         for(int i=;i<;i++){
             int nx=mx+xx[i],ny=my+yy[i];
             if(nx< || ny< || nx>n || ny>m || (c[nx][ny]>='' && c[nx][ny]<='') || c[nx][ny]=='#') continue;
             int ns=ms;
             if(i&) ns=solve(mx,my,nx,ny,ms);
             if(f[mx][my][ms]<f[nx][ny][ns]){
                 f[nx][ny][ns]=f[mx][my][ms]+;
                 if(vis[nx][ny][ns]==){
                     vis[nx][ny][ns]=;
                     q.push(asd(nx,ny,ns));
                 }
             }
         }
     }
     for(int i=;i<mmax;i++){
         ans=max(ans,val[i]-f[ii][jj][i]);
     }
 }
 int main(){
     scanf("%d%d%d",&n,&m,&d);
     for(int i=;i<=d;i++){
         scanf("%d",&da[i]);
     }
     mmax=<<d;
     for(int i=;i<mmax;i++){
         for(int j=;j<=d;j++){
             if(i&(<<(j-))) val[i]+=da[j];
         }
     }
     for(int i=;i<=n;i++){
         scanf("%s",c[i]+);
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]>'' && c[i][j]<=''){
                 int now=c[i][j]-'';
                 ax[now]=i,ay[now]=j;
             }
         }
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]==''){
                 SPFA(i,j);
             }
         }
     }
     printf("%d\n",ans);
     return ;
 }

SPFA

大家一定要注意vis数组的初始化

而且数组不要开太大，否则会T

下面是一个错解，也就是bfs的vis数组没有初始化

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cstring>
 using namespace std;
 int n,m,d;
 int mmax,f[][][<<],da[],val[<<];
 struct asd{
     int x,y,s;
     asd(int aa=,int bb=,int cc=){
         x=aa,y=bb,s=cc;
     }
 };//跑bfs的结构体
 char c[][];
 int xx[]={,-,,},yy[]={-,,,},ax[],ay[];
 //xx,yy枚举走的方向，ax,ay记录豆豆的横纵坐标
 int ans=-0x3f3f3f3f;//记录最终价值
 int vis[][][<<];//判断该点是否已经遍历过
 int solve(int mx,int my,int nx,int ny,int ms){
     int ns=ms;
     for(int i=;i<=d;i++){
         if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){
             ns^=(<<(i-));
         }
     }
     return ns;
 }
 void bfs(int ii,int jj){
     queue<asd> q;
     q.push(asd(ii,jj,));
     memset(f,0x3f,sizeof(f));
     f[ii][jj][]=;
     while(!q.empty()){
         asd aa=q.front();
         q.pop();
         int mx=aa.x,my=aa.y,ms=aa.s;
         vis[mx][my][ms]=;
         for(int i=;i<;i++){
             int nx=mx+xx[i],ny=my+yy[i];
             if(nx< || ny< || nx>n || ny>m || (c[nx][ny]>='' && c[nx][ny]<='') || c[nx][ny]=='#') continue;
              //判断该点是否能走
             //注意豆豆所在的方格也不能走
             int ns=ms;
             if(i&) ns=solve(mx,my,nx,ny,ms);
             //只有在上下走的时候才改变状态，否则状态不变
             //如果不能理解也可以写成i==1 || i==3
             if(vis[nx][ny][ns]==) continue;
             //如果已经更新过，就不再更新
             if(f[mx][my][ms]<f[nx][ny][ns]){
                 f[nx][ny][ns]=f[mx][my][ms]+;
                 if(vis[nx][ny][ns]==){
                     vis[nx][ny][ns]=;
                     q.push(asd(nx,ny,ns));
                 }
             }
         }
     }
     for(int i=;i<mmax;i++){
         ans=max(ans,val[i]-f[ii][jj][i]);
     }
 }
 int main(){
     scanf("%d%d%d",&n,&m,&d);
     for(int i=;i<=d;i++){
         scanf("%d",&da[i]);
     }
     mmax=<<d;
     for(int i=;i<mmax;i++){
         for(int j=;j<=d;j++){
             if(i&(<<(j-))) val[i]+=da[j];
         }
     }
     for(int i=;i<=n;i++){
         scanf("%s",c[i]+);
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]>'' && c[i][j]<=''){
                 int now=c[i][j]-'';
                 ax[now]=i,ay[now]=j;
             }
         }
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(c[i][j]==''){
                 bfs(i,j);
                 //如果该点为0，就可以作为起点
             }
         }
     }
     printf("%d\n",ans);
     return ;
 }

错解

但是令人震惊的是，它竟然能过，而且比正解快10倍，只用70ms

引用pl.er()大佬的思路

它之所以快是因为第一次遍历之后vis数组没有初始化，于是在之后的遍历中它们就不会再进栈

但是这样做显然是错误的，比如下面这组数据

正解是992，但是错解却输出990

因此大家一定要注意