Reachability from the Capital(Codeforces Round #490 (Div. 3)+tarjan有向图缩点）

题目链接：http://codeforces.com/contest/999/problem/E

题目：

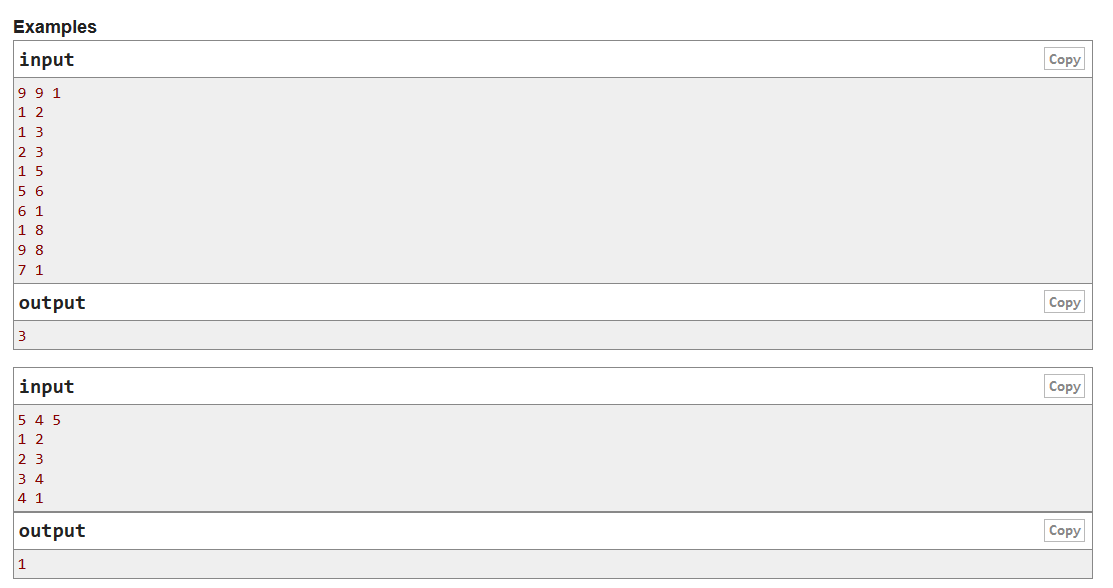
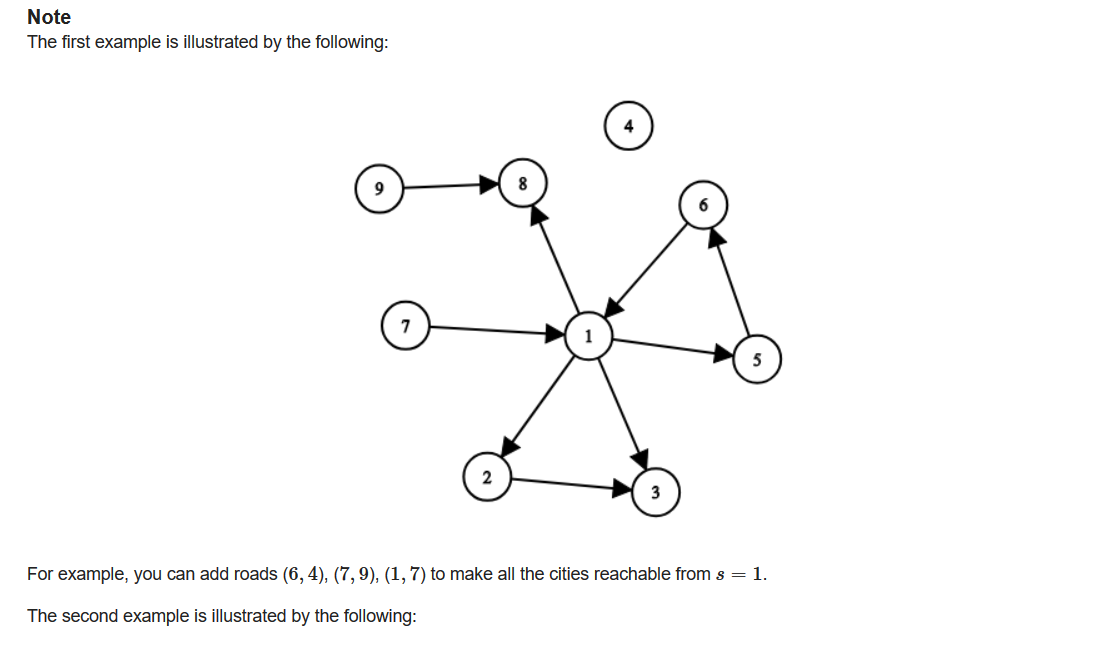
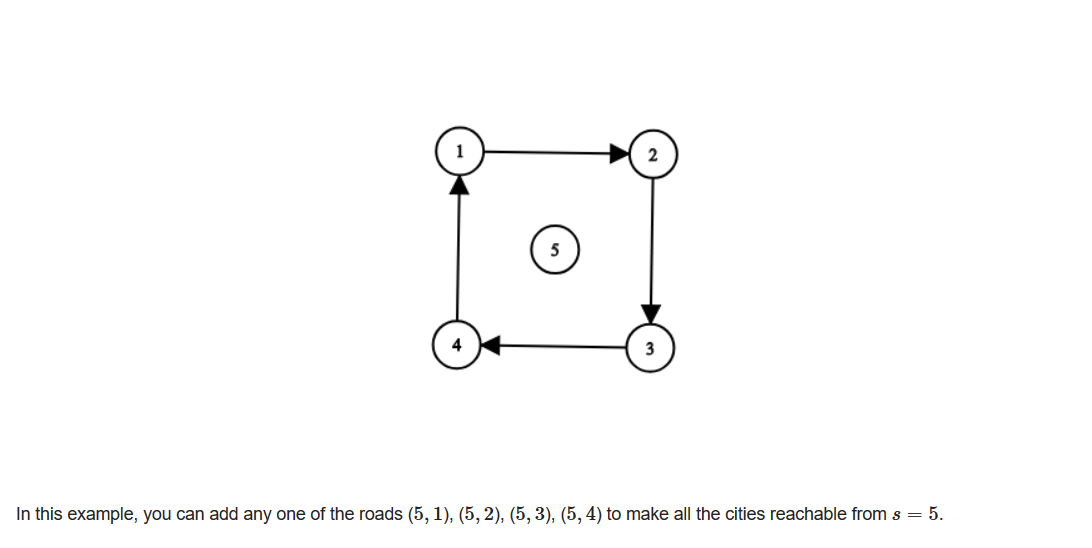
题意：给你n个城市，m条单向边，问你需要加多少条边才能使得从首都s出发能到达任意一个城市。

思路：tarjan缩点，结果就是缩点新建的图中入度为0的点的数量。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 5e3 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int n, m, tot, s, cnt, top, u, v, num;
 int head[maxn], vis[maxn], in[maxn];
 int tot1, head1[maxn], in1[maxn];
 int dfn[maxn], low[maxn], c[maxn], stc[maxn];

 struct edge {
     int v, next;
 }ed[maxn], ed1[maxn];

 void addedge(int u, int v) {
     ed[tot].v = v;
     ed[tot].next = head[u];
     head[u] = tot++;
 }

 void addedge1(int u, int v) {
     ed1[tot1].v = v;
     ed1[tot1].next = head1[u];
     head1[u] = tot1++;
 }

 void tarjan(int x) {
     dfn[x] = low[x] = ++num;
     vis[x] = , stc[++top] = x;
     for(int i = head[x]; ~i; i = ed[i].next) {
         int y = ed[i].v;
         if(!dfn[y]) {
             tarjan(y);
             low[x] = min(low[x], low[y]);
         } else if(vis[y]) {
             low[x] = min(low[x], low[y]);
         }
     }
     if(dfn[x] == low[x]) {
         int y; cnt++;
         do {
             y = stc[top--]; vis[y] = ;
             c[y] = cnt;
         } while(x != y);
     }
 }

 int main() {
     //FIN;
     scanf("%d%d%d", &n, &m, &s);
     memset(head, -, sizeof(head));
     memset(head1, -, sizeof(head1));
     for(int i = ; i <= m; i++) {
         scanf("%d%d", &u, &v);
         addedge(u, v);
         in[v]++;
     }
     for(int i = ; i <= n; i++) {
         if(in[i] ==  && !dfn[i]) {
             tarjan(i);
         }
     }
     for(int i = ; i <= n; i++) {
         if(!dfn[i]) {
             tarjan(i);
         }
     }
     int sum = ;
     for(int i = ; i <= n; i++) {
         for(int j = head[i]; ~j; j = ed[j].next) {
             int y = ed[j].v;
             if(c[i] == c[y]) continue;
             addedge1(c[i], c[y]);
             in1[c[y]]++;
         }
     }
     s = c[s];
     for(int i = ; i <= cnt; i++) {
         if(i != s && in1[i] == ) {
             sum++;
         }
     }
     printf("%d\n", sum);
     return ;
 }