【Foreign】Bumb [模拟退火]

Bumb

Time Limit: 20 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

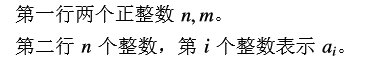
Output

　　

Sample Input

　　4
　　1 5 1 4

Sample Output

　　5

HINT

　　

Solution

　　首先，我们对于一个已知的k，可以O(n)得到Ans，这样就有60%了。

　　那么怎么做90%呢？老老实实写O(nlogn)是不可能的！模拟退火美滋滋！

　　传授一点人生的经验吧：写个对拍用于调参，由于这种题不能很单峰，显然温度变化设大一点比较容易正确，无限running + 卡时即可。

　　是的，没有错！BearChild就这样拿到了90%！

　　我们来考虑100%怎么做，显然复杂度O(n)。我们把( a[i - 1], a[i] ]看作若干个区间挂在数轴上。

　　然后考虑k：1->m对于答案的变化。显然可以记录cnt表示k包含的区间个数，以及sum和，这样就可以做完啦！

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<vector>
 #include<ctime>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const s64 INF = 1e18;

 int n, m;
 int a[ONE];
 int Now, A;
 s64 Ans = INF;

 int get()
 {
         int res=,Q=;char c;
         while( (c=getchar())< || c> )
         if(c=='-')Q=-;
         res=c-;
         while( (c=getchar())>= && c<= )
         res=res*+c-;
         return res*Q;
 }

 void TimeE()
 {
         if((double)clock() / CLOCKS_PER_SEC > 0.97)
         {
             printf("%lld", Ans);
             exit();
         }
 }

 s64 Get(int x, int y)
 {
         TimeE();
         if(x <= y) return y - x;
         return y + m - x;
 }

 s64 Judge(int k)
 {
         s64 res = ;
         for(int i = ; i <= n; i++)
             res += min(Get(a[i - ], a[i]),  + Get(k, a[i]));
         Ans = min(Ans, res);
         return res;
 }

 double Random() {return rand() / (double)RAND_MAX;}
 void SA(double T)
 {
         Now = m / ;
         while(T >= )
         {
             A = Now + (int)(T * (Random() *  - ));
             if(A <  || A > m) A = T * Random();
             s64 dE = Judge(A) - Judge(Now);
             if(dE < ) Now = A;
             T *= 0.92;
         }
 }

 int main()
 {
         n = get();    m = get();
         for(int i = ; i <= n; i++)
             a[i] = get();
         if(n > ) {for(;;)SA(m); return ;}

         for(int i = ; i <= m; i++)
             Ans = min(Ans, Judge(i));

         printf("%lld", Ans);
 }

模拟退火 90%

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<vector>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const s64 INF = 1e18;

 int n, m;
 int a[ONE];
 int L[ONE];
 vector <int> R[ONE];
 s64 Ans;

 int get()
 {
         int res=,Q=;char c;
         while( (c=getchar())< || c> )
         if(c=='-')Q=-;
         res=c-;
         while( (c=getchar())>= && c<= )
         res=res*+c-;
         return res*Q;
 }

 int Get(int x, int y)
 {
         if(x <= y) return y - x;
         return y + m - x;
 }

 int main()
 {
         n = get();    m = get();
         for(int i = ; i <= n; i++)
             a[i] = get();

         for(int i = ; i <= n; i++)
         {
             Ans += Get(a[i - ], a[i]);
             L[a[i - ]]++, R[a[i]].push_back(a[i - ]);
         }

         s64 sum = Ans, cnt = ;

         for(int i = ; i <= n; i++)
             if(a[i - ] > a[i])
                 sum -= m - a[i - ], cnt++;

         for(int k = ; k <= m; k++)
         {
             int len = R[k - ].size();
             cnt = cnt + L[k - ] - len;
             sum -= cnt;
             for(int i = ; i < len; i++)
                 sum += Get(R[k - ][i], k - ) - ;
             Ans = min(Ans, sum);
         }

         printf("%lld", Ans);
 }

正解 100%