C基础 工程中常用的排序

引言 - 从最简单的插入排序开始

　　很久很久以前, 也许都曾学过那些常用的排序算法. 那时候觉得计算机算法还是有点像数学.

可是脑海里常思考同类问题, 那有什么用呢(屌丝实践派对装逼学院派的深情鄙视). 不可能让你去写.

都封装的那么好了. n年后懂了点, 学那是为了用的, 哪有什么目的, 有的是月落日升, 风吹云动~ ＿φ( °-°)/

　　本文会举一些实践中排序所用的地方, 解析那些年用过的排序套路,  这里先来个插入排序

// 插入排序
void
sort_insert(int a[], int len) {
    int i, j;

    for (i = ; i < len; ++i) {
        int tmp = a[i];
        for (j = i; j > ; --j) {
            if (tmp >= a[j - ])
                break;
            a[j] = a[j - ];
        }
        a[j] = tmp;
    }
}

插入排序在小型数据排序中很常用! 也是链式结构首选排序算法. 插入排序超级进化 -> 希尔排序, O(∩_∩)O哈哈~.

unsafe code 很需要测试框架, 这里为本文简单写了个测试套路如下

void array_rand(int a[], int len);
void array_print(int a[], int len);

//
// ARRAY_TEST - 方便测试栈上数组, 关于排序相关方面
//
#define ARRAY_TEST(a, fsort) \
    array_test(a, sizeof(a) / sizeof(*(a)), fsort)

inline void array_test(int a[], int len, void(* fsort)(int [], int)) {
    assert(a && len >  && fsort);
    array_rand(a, len);
    array_print(a, len);
    fsort(a, len);
    array_print(a, len);
}

// 插入排序
void sort_insert(int a[], int len);

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

#define _INT_ARRAY    (64)
//
// test sort base, sort is small -> big
//
int main(int argc, char * argv[]) {
    int a[_INT_ARRAY];

    // 原始数据 + 插入排序
    ARRAY_TEST(a, sort_insert);

    return EXIT_SUCCESS;
}

#define _INT_RANDC (200)
void
array_rand(int a[], int len) {
    for (int i = ; i < len; ++i)
        a[i] = rand() % _INT_RANDC;
}
#undef _INT_SORTC

#define _INT_PRINT (26)
void
array_print(int a[], int len) {
    int i = ;
    printf("now array[%d] current low:\n", len);
    while(i < len) {
        printf("%4d", a[i]);
        if (++i % _INT_PRINT == )
            putchar('\n');
    }
    if (i % _INT_PRINT)
        putchar('\n');
}
#undef _INT_PRINT

单元测试(白盒测试)是工程质量的保证, 否则自己都害怕自己的代码. 软件功底2成在于测试功力是否到位.

顺带扯一点上面出现系统随机函数 rand, 不妨再多说一点, 下面是最近写的48位随机算法 scrand

　　scrand https://github.com/wangzhione/simplec/blob/master/simplec/module/schead/scrand.c

它是从redis上拔下来深加工的随机算法, 性能和随机性方面比系统提供的要好. 最大的需求是平台一致性.

有机会单独开文扯随机算法, 水也很深. 毕竟随机算法是计算机史上十大重要算法, 排序也是.

　　一开始介绍插入排序,  主要为了介绍系统内置的混合排序算法 qsort. qsort 多数实现是

quick sort + small insert sort. 那快速排序是什么样子呢, 看如下一种高效实现

// 快速排序
void sort_quick(int a[], int len);

// 快排分区, 按照默认轴开始分隔
static int _sort_quick_partition(int a[], int si, int ei) {
    int i = si, j = ei;
    int par = a[i];
    while (i < j) {
        while (a[j] >= par && i < j)
            --j;
        a[i] = a[j];

        while (a[i] <= par && i < j)
            ++i;
        a[j] = a[i];
    }
    a[j] = par;
    return i;
}

// 快速排序的核心代码
static void _sort_quick(int a[], int si, int ei) {
    if (si < ei) {
        int ho = _sort_quick_partition(a, si, ei);
        _sort_quick(a, si, ho - );
        _sort_quick(a, ho + , ei);
    }
}

// 快速排序
inline void
sort_quick(int a[], int len) {
    _sort_quick(a, , len - );
}

这里科普一下为啥把 _sort_quick_partition 单独封装出来. 主要原因是 _sort_quick 是个递归函数,

占用系统函数栈, 单独分出去, 系统占用的栈大小小一点. 轻微提高安全性. 看到这里, 希望以后遇到别人

聊基础也能扯几句了,  高效的操作多数是应环境而多种方式的组合取舍. 突然感觉我们还能翻~

前言 - 来个奇妙的堆排序

　　堆排序的思路好巧妙, 构建二叉树'记忆'的性质来处理排序过程中的有序性. 它是冒泡排序的超级进化.

总的套路可以看成下面这样数组索引 [0, 1, 2, 3, 4, 5, 6, 7, 8] - >

0, 1, 2 一个二叉树, 1, 3, 4 一个二叉树, 2, 5, 6一个二叉树, 3, 7, 8 一个树枝.  直接看代码, 感悟以前神的意志

// 大顶堆中加入一个父亲结点索引, 重新构建大顶堆
static void _sort_heap_adjust(int a[], int len, int p) {
    int node = a[p];
    int c =  * p + ; // 先得到左子树索引
    while (c < len) {
        // 如果有右孩子结点, 并且右孩子结点值大, 选择右孩子
        if (c +  < len && a[c] < a[c + ])
            c = c + ;

        // 父亲结点就是最大的, 那么这个大顶堆已经建立好了
        if (node > a[c])
            break;

        // 树分支走下一个结点分支上面
        a[p] = a[c];
        p = c;
        c =  * c + ;
    }
    a[p] = node;
}

// 堆排序
void
sort_heap(int a[], int len) {
    int i = len / ;
    // 线初始化一个大顶堆出来
    while (i >= ) {
        _sort_heap_adjust(a, len, i);
        --i;
    }

    // n - 1 次调整, 排好序
    for (i = len - ; i > ; --i) {
        int tmp = a[i];
        a[i] = a[];
        a[] = tmp;

        // 重新构建堆数据
        _sort_heap_adjust(a, i, );
    }
}

堆排序单独讲一节, 在于它在基础件开发应用中非常广泛. 例如有些定时器采用小顶堆结构实现,

快速得到最近需要执行的结点. 堆结构也可以用于外排序. 还有堆在处理范围内极值问题特别有效.

后面我们会运用堆排序来处理个大文件外排序问题.

/*
 问题描述:
      存在个大文件 data.txt , 保存着 int \n ... 这种格式数据. 是无序的.
 目前希望从小到大排序并输出数据到 ndata.txt 文件中

 限制条件:
      假定文件内容特别多, 无法一次加载到内存中.
      系统最大可用内存为 600MB以内.
 */

正文 - 来个实际的外排序案例

　　这里不妨来解决上面这个问题, 首先是构建数据. 假定'大数据'为 data.txt. 一个 int 加 char 类型,

重复输出 1<<28次, 28位 -> 1.41 GB (1,519,600,600 字节) 字节.

#define _STR_DATA        "data.txt"
// 28 -> 1.41 GB (1,519,600,600 字节) | 29 -> 2.83 GB (3,039,201,537 字节)
#define _UINT64_DATA    (1ull << 28)

static FILE * _data_rand_create(const char * path, uint64_t sz) {
    FILE * txt = fopen(path, "wb");
    if (NULL == txt) {
        fprintf(stderr, "fopen wb path error = %s.\n", path);
        exit(EXIT_FAILURE);
    }

    for (uint64_t u = ; u < sz; ++u) {
        int num = rand();
        fprintf(txt, "%d\n", num);
    }

    fclose(txt);
    txt = fopen(path, "rb");
    if (NULL == txt) {
        fprintf(stderr, "fopen rb path error = %s.\n", path);
        exit(EXIT_FAILURE);
    }

    return txt;
}

以上就是数据构建过程. 要多大只需要调整宏大小. 太大时间有点长. 处理问题的思路是

    . 数据切割成合适份数N
    . 每份内排序, 从小到大, 并输出到特定文件中
    . 采用N大小的小顶堆, 挨个读取并输出, 记录索引
    . 那个索引文件输出, 那个索引文件输入, 最终输出一个排序好的文件

第一步操作切割数据, 分别保存在特定序列文件中

#define _INT_TXTCNT    (8)

static int _data_txt_sort(FILE * txt) {
    char npath[];
    FILE * ntxt;
    // 需要读取的数据太多了, 直接简单监测一下, 数据是够构建完毕
    snprintf(npath, sizeof npath, "%d_%s", _INT_TXTCNT, _STR_DATA);
    ntxt = fopen(npath, "rb");
    if (ntxt == NULL) {
        int tl, len = (int)(_UINT64_DATA / _INT_TXTCNT);
        int * a = malloc(sizeof(int) * len);
        if (NULL == a) {
            fprintf(stderr, "malloc sizeof int len = %d error!\n", len);
            exit(EXIT_FAILURE);
        }

        tl = _data_split_sort(txt, a, len);

        free(a);

        return tl;
    }

    return _INT_TXTCNT;
}

切割成八份, 每份也就接近200MB. 完整的构建代码如下

// 堆排序
void sort_heap(int a[], int len);

// 返回分隔的文件数
static int _data_split_sort(FILE * txt, int a[], int len) {
    int i, n, rt = , ti = ;
    char npath[];
    FILE * ntxt;

    do {
        // 得到数据
        for (n = ; n < len; ++n) {
            rt = fscanf(txt, "%d\n", a + n);
            if (rt != ) {
                // 读取已经结束
                break;
            }
        }

        if (n == )
            break;

        // 开始排序
        sort_heap(a, n);

        // 输出到文件中
        snprintf(npath, sizeof npath, "%d_%s", ++ti, _STR_DATA);
        ntxt = fopen(npath, "wb");
        if (NULL == ntxt) {
            fprintf(stderr, "fopen wb npath = %s error!\n", npath);
            exit(EXIT_FAILURE);
        }
        for (i = ; i < n; ++i)
            fprintf(ntxt, "%d\n", a[i]);
        fclose(ntxt);
    } while (rt == );

    return ti;
}

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>

//
// 大数据排序数据验证
//
int main(int argc, char * argv[]) {
    int tl;
    FILE * txt = fopen(_STR_DATA, "rb");

    puts("开始构建测试数据 _data_rand_create");
    // 开始构建数据
    if (NULL == txt)
        txt = _data_rand_create(_STR_DATA, _UINT64_DATA);

    puts("数据已经到位, 开始分隔数据进行排序");
    tl = _data_txt_sort(txt);
    fclose(txt);

    // 这里分拨的数据构建完毕, 开始外排序过程

    return EXIT_SUCCESS;
}

执行上面切割代码, 最终生成会得到如下数据内容

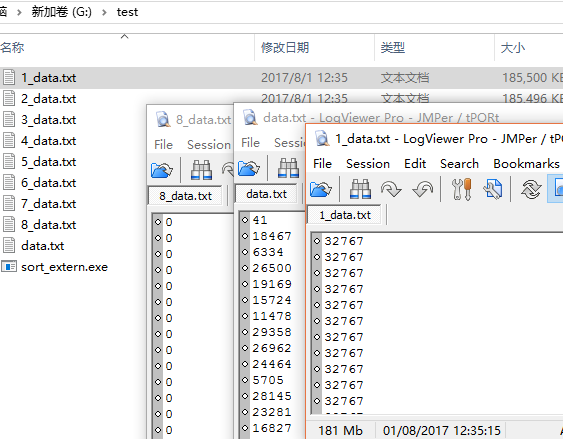
1 - 8 _data.txt 数据是分隔排序后输出数据. 随后载开始处理数据进行外排序输出最终结果文件.

struct node {
    FILE * txi;    // 当前是那个文件的索引
    int val;    // 读取的值
};

// true表示读取完毕, false可以继续读取
static bool _node_read(struct node * n) {
    assert(n && n->txi);
    return  != fscanf(n->txi, "%d\n", &n->val);
}

// 建立小顶堆
static void _node_minheap(struct node a[], int len, int p) {
    struct node node = a[p];
    int c =  * p + ; // 先得到左子树索引
    while (c < len) {
        // 如果有右孩子结点, 并且右孩子结点值小, 选择右孩子
        if (c +  < len && a[c].val > a[c + ].val)
            c = c + ;

        // 父亲结点就是最小的, 那么这个小顶堆已经建立好了
        if (node.val < a[c].val)
            break;

        // 树分支走下一个结点分支上面
        a[p] = a[c];
        p = c;
        c =  * c + ;
    }
    a[p] = node;
}

struct output {
    FILE * out;    // 输出数据内容
    int cnt;    // 存在具体多少文件内容
    struct node a[];
};

// 数据销毁和构建初始化
void output_delete(struct output * put);
struct output * output_create(int cnt, const char * path);
// 开始排序构建
void output_sort(struct output * put);

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>

#define _INT_TXTCNT        (8)
#define _STR_DATA        "data.txt"
#define _STR_OUTDATA    "output.txt"

//
// 对最终生成数据进行一种外排序尝试
//
int main(int argc, char * argv[]) {
    // 构建操作内容
    struct output * put = output_create(_INT_TXTCNT, _STR_OUTDATA);

    output_sort(put);

    // 数据销毁
    output_delete(put);
    return EXIT_SUCCESS;
}

以上是处理的总流程, 对于构建和销毁部分展示在下面

void
output_delete(struct output * put) {
    if (put) {
        for (int i = ; i < put->cnt; ++i)
            fclose(put->a[i].txi);
        free(put);
    }
}

struct output *
output_create(int cnt, const char * path) {
    FILE * ntxt;
    struct output * put = malloc(sizeof(struct output) + cnt * sizeof(struct node));
    if (NULL == put) {
        fprintf(stderr, "_output_init malloc cnt = %d error!\n", cnt);
        exit(EXIT_FAILURE);
    }

    put->cnt = ;
    for (int i = ; i < cnt; ++i) {
        char npath[];
        // 需要读取的数据太多了, 直接简单监测一下, 数据是够构建完毕
        snprintf(npath, sizeof npath, "%d_%s", _INT_TXTCNT, _STR_DATA);
        ntxt = fopen(npath, "rb");
        if (ntxt) {
            put->a[put->cnt].txi = ntxt;
            // 并初始化一下数据
            if (_node_read(put->a + put->cnt))
                fclose(ntxt);
            else
                ++put->cnt;
        }
    }

    // 这种没有意义, 直接返回数据为empty
    if (put->cnt <= ) {
        free(put);
        exit(EXIT_FAILURE);
    }

    // 构建数据
    ntxt = fopen(path, "wb");
    if (NULL == ntxt) {
        output_delete(put);
        fprintf(stderr, "fopen path cnt = %d, = %s error!\n", cnt, path);
        exit(EXIT_FAILURE);
    }
    put->out = ntxt;

    return put;
}

核心排序算法 output_sort ,

// 28 -> 1.41 GB (1,519,600,600 字节) | 29 -> 2.83 GB (3,039,201,537 字节)
#define _UINT64_DATA    (1ull << 28)

// 开始排序构建
void
output_sort(struct output * put) {
    int i, cnt;
    uint64_t u = ;
    assert(put && put->cnt > );

    cnt = put->cnt;
    // 开始构建小顶堆
    i = cnt / ;
    while (i >= ) {
        _node_minheap(put->a, cnt, i);
        --i;
    }

    while (cnt > ) {
        ++u;
        // 输出数据, 并且重新构建数据
        fprintf(put->out, "%d\n", put->a[].val);
        if (_node_read(put->a)) {
            --cnt;
            // 交换数据, 并排除它
            struct node tmp = put->a[];
            put->a[] = put->a[cnt];
            put->a[cnt] = tmp;
        }
        _node_minheap(put->a, cnt, );
    }

    // 输出最后文件内容, 输出出去
    do {
        ++u;
        fprintf(put->out, "%d\n", put->a[].val);
    } while (!_node_read(put->a));

    printf("src = %llu, now = %llu, gap = %llu.\n", _UINT64_DATA, u, _UINT64_DATA - u);
}

最终得到数据 output.txt

以上就是咱们常被面试过程中问及的大数据瞎搞问题, 一种简陋的解决方案. 当然事情远远才刚刚开始!

学生阶段面试吹一波感觉是可以了~ 扯一点, 年轻时候多吹一点NB, 以后也就只能看着别人~

后记 - 等我回家

　　等我回家 - http://music.163.com/#/song?id=477890886

　　

　　最近很羡慕陈胜吴广, 未来深不可测. 假如我们都是直男癌, 一定不要忘记有过的血气方刚 ~