2017 icpc 西安网络赛

F. Trig Function

样例输入

2 0
2 1
2 2

样例输出

998244352
0
2

---

找啊找啊找数列和论文。cosnx可以用切比雪夫多项式弄成（cosx）的多项式，然后去找到了相关的公式：

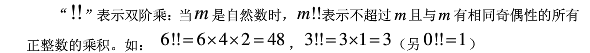
然后写个快速幂预处理啥的，很快就解决了~

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 #define mod 998244353
 using namespace std;
 LL jc[],djc[];
 LL n,m,k,ans;
 LL quick_pow(LL x,LL n)
 {
     LL res=;
     x=(x%mod+mod)%mod;
     while(n)
     {
         if(n&)
             res=res*x%mod;
         x=x*x%mod;
         n>>=;
     }
     return res;
 }

 void init()
 {
     jc[]=jc[]=;
     for(int i=;i<=;i++)
         jc[i]=(jc[i-]*i)%mod;
     djc[]=quick_pow(jc[],mod-);
     for(int i=;i>=;i--)
         djc[i]=djc[i+]*(i+)%mod;
     djc[]=;
     return ;
 }
 int main()
 {
     init();
     while(scanf("%lld%lld",&n,&m)!=EOF)
     {
         if(m>n || m< || (n-m)%!=)
         {
             printf("0\n");
             continue;
         }
         ans=(n-m)/%==?-:;
         ans=(ans*djc[m]*n%mod+mod)%mod;
         if(n-m<=n+m-)
             for(LL i=n-m+;i<=n+m-;i+=)
                 ans=ans*(i%mod)%mod;
         else
             for(LL i=n-m;i>n+m-;i-=)
                 ans=ans*quick_pow(i,mod-)%mod;
         printf("%lld\n",ans);
     }
     return ;
 }

E。 Maximum Flow

样例输入

2

样例输出

1

---

这题可以用最大流最小割推推，但我~找规律的2333。

首先是2^k的n(默认n--了)，那么所有的从0出来的流都能到达终点，也就是流量为（n+1）*n/2。然后写个最大流打个表，然后将i和i-1作差。可以发现在2^k~2^(k+1)的数中，差为2（2^0+1）每隔2个出现，差为5（2^2+1）每隔4个出现，17（2^4+1）每隔8个出现。。。依此类推。然后你懂得~。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define LL long long
 #define mod 1000000007
 using namespace std;
 LL quick_pow(LL x, LL n) {
     LL res = ;
     x=(x%mod+mod)%mod;
     while(n) {
         if(n&)
             res=res*x% mod;
         n >>=;
         x =x*x% mod;
     }
     return res;
 }
 int main()
 {
     LL n,m,q,l,ans,k,kk;
     int t;
     while(scanf("%lld",&n)!=EOF)
     {
         t=;
         n--;
         m=n;
         while(m)
         {
             t++;
             m>>=;
         }
         q=;
         m=(q<<(t-));
         ans=(m%mod)*((+m)%mod)%mod;
         ans=ans*quick_pow(,mod-)%mod;
         n-=m;
         kk=;
         k=;
         while(k<=n+kk)
         {
             ans=(ans%mod+(((n+kk)/k)%mod)*((kk%mod)*(kk%mod)%mod+)%mod)%mod;
             if(k==LLONG_MAX)
                 break;
             kk=k;
             k<<=;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

C.Sum

样例输入

1
1

样例输出

89999999999999999999999999

---

输入啥都输出233个9就行了。k个9无论乘多少数位和仍是k*9。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clr_1(x) memset(x,-1,sizeof(x))
 #define LL long long
 using namespace std;
 int main()
 {
     LL n,m,k;
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lld",&n);
         for(int i=;i<=;i++)
             printf("");
         printf("\n");
     }
     return ;
 }

B.Coin

样例输入

2
2 1 1
3 1 2

样例输出

500000004
555555560

---

23333，n重伯努利实验概率分布题。
设q=1-p,p为事件概率。
Y为出现偶数次的概率。

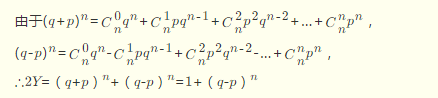
所以Y=(1+(q-p)^n)/2,求个逆元啥的，快速幂啥的就能做出来了。

 #include<bits/stdc++.h>
 #define LL long long
 #define mod 1000000007
 using namespace std;
 LL quick_pow(LL x, LL n) {
     LL res = ;
     x=(x%mod+mod)%mod;
     while(n) {
         if(n&)
             res=res*x% mod;
         n >>=;
         x =x*x% mod;
     }
     return res;
 }
 int main()
 {
     LL p, q;
     LL n;
     int t;
     scanf("%d", &t);
     while(t --) {
         scanf("%lld%lld%lld",&p, &q, &n);
         LL a=quick_pow(p,mod-);
         a=(a**q)%mod;
         a=(-a+mod)%mod;
         a=quick_pow(a,n)%mod;
         a=(a+)%mod;
         LL b=quick_pow(,mod-)%mod;
         a=(a*b)%mod;
         printf("%lld\n", (a%mod+mod)%mod);
     }
 }