【题解】洛谷P3435 [POI2006] OKR-Periods of Words（KMP）

洛谷P3435：https://www.luogu.org/problemnew/show/P3435

思路

来自Kamijoulndex大佬的解释

先把题面转成人话：

对于给定串的每个前缀i，求最长的，使这个字符串重复两遍能覆盖原前缀i的前缀（就是前缀i的一个前缀），求所有的这些“前缀的前缀”的长度和

因为前缀i长度为p[i]的前缀和后缀相同

这说明：如果i有一个公共前后缀长度为j，那么这个前缀i就有一个周期为i-j

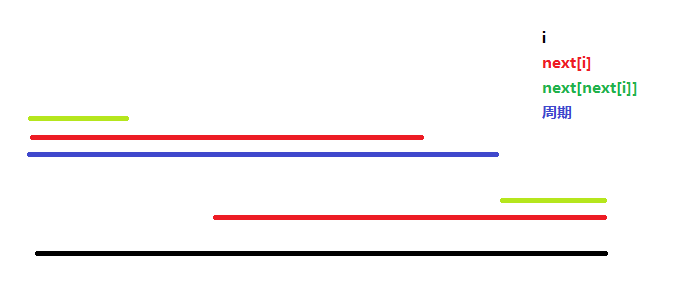
显然 图中蓝色线段是黑色线段的一个周期

那么我们先预处理出P数组

对于每个前缀i 我们令j=i 在j>0是不断查询j=p[j] 使j变得越来越小

则周期i-j就会越来越大

最后ans+=i-j

感谢dalao的思路orzorz

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 1000010
char a[maxn];
int p[maxn];
int len,j;
long long ans;
int main()
{
    scanf("%d",&len);
    scanf("%s",a+);
    for(int i=;i<=len;i++)//常规KMP
    {
        while(j&&a[j+]!=a[i]) j=p[j];
        if(a[j+]==a[i]) j++;
        p[i]=j;
    }
    for(int i=;i<=len;i++)//对每个前缀
    {
        j=i;//令j=i
        while(p[j]) j=p[j];//不断缩小j
        if(p[i]!=) p[i]=j;//记忆化
        ans+=i-j;//累计ans
    }
    printf("%lld",ans);
}