JZOJ.5236【NOIP2017模拟8.7】利普希茨
Description
Input
第一行一个整数n。
接下来一行n个整数,描述序列A。
第三行一个数q 。
接下来q行,每行三个整数。其中第一个整数type表示操作的类型。 type=0对应修改操作, type=1对应查询操作。
Output
对于每个查询,给出f(A[l..r]) 。
Sample Input
- 输入1:
- 6
- 90 50 78 0 96 20
- 6
- 0 1 35
- 1 1 4
- 0 1 67
- 0 4 11
- 0 3 96
- 1 3 5
- 输入2:
- 50
- 544 944 200 704 400 150 8 964 666 596 850 608 452 103 988 760 370 723 350 862 856 0 724 544 668 891 575 448 16 613 952 745 990 459 740 960 752 194 335 575 525 12 618 80 618 224 240 600 562 283
- 10
- 1 6 6
- 1 1 3
- 0 11 78279
- 0 33 42738
- 0 45 67270
- 1 1 26
- 1 19 24
- 1 37 39
- 1 8 13
- 0 7 64428
Sample Output
- 输出1:
- 78
- 85
- 输出2:
- 0
- 744
- 77683
- 856
- 558
- 77683
Data Constraint
对于60%的数据,n,q<=5000
对于100%的数据,n,q<=100000,0<=ai,val<=10^9
这里有一个结论:f(A)的最大值是相邻的两点的差值。
我们可以设想一下,一个区间被里面min和max分成了三段,其中i=min,j=max,那么设对应的f(A)的值为a,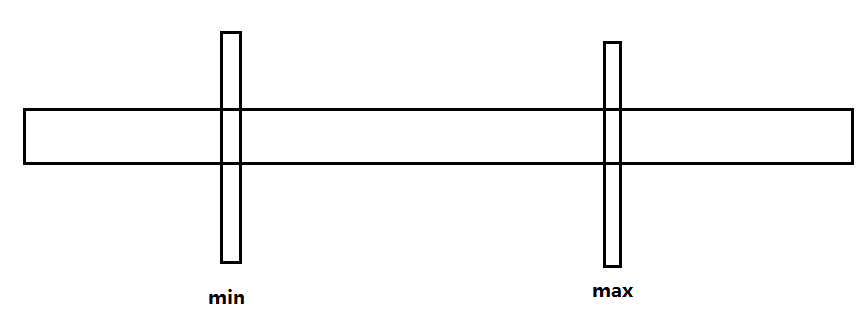
那么我们可以枚举里面的左端点i右端点j来计算f(A)的值与a比较
首先很肯定的一点 区间[i,j]不能跨过min和max,那么我们会对这三段区间不断细分,到最后也就只剩下相邻的两个点了,此时就是最大值和最小值(这个似乎不能证明)
还有个几何证明:f(A)可以看成一个斜率的绝对值,那么对于坐标上的三个点a,b,c来说,它们三点确定的直线中,很显然横坐标越靠近的两个点斜率会越大
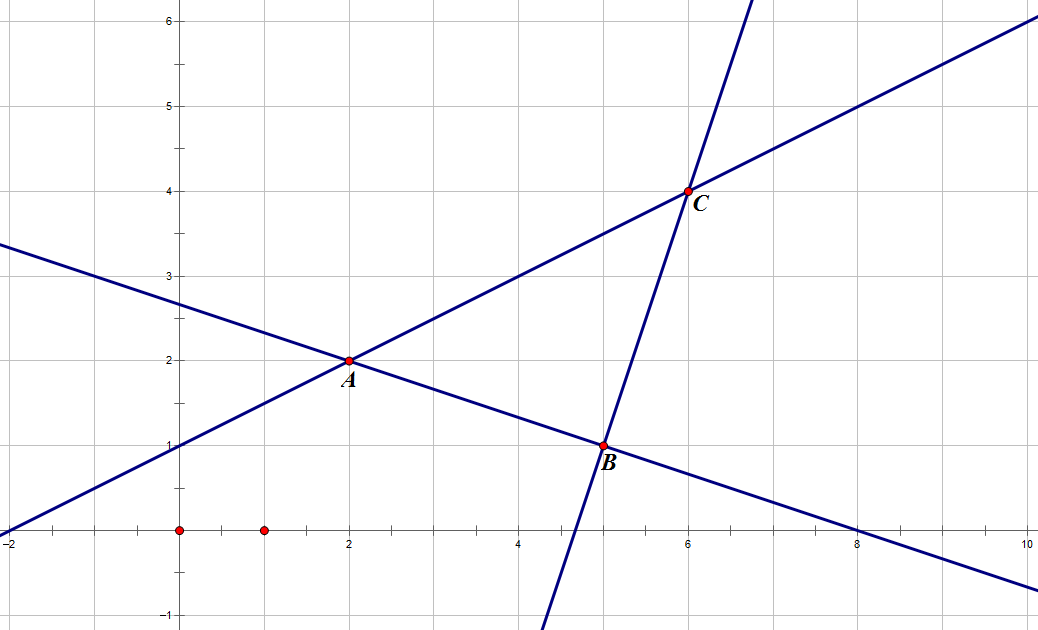
(转自mcw的证明)令$\Delta_i=A_{i+1}-A_i$,则$\left\lceil\frac{|A_j-A_i|}{j-i}\right\rceil=\left\lceil\frac{|\sum_{k=i}^{j-1}\Delta_k|}{j-i}\right\rceil=\overline{\Delta_{i\,..\,j-1}}$,显然会有$\Delta_i\,..\,\Delta_{j-1}$中的一项大于等于$\overline{\Delta_{i\,..\,j-1}}$
所以这题就变成了维护差值的修改和最值了,线段树就可以了。
- #include<iostream>
- #include<cstdio>
- #include<cstring>
- #include<algorithm>
- #include<cstdlib>
- #include<cmath>
- using namespace std;
- int maxx[],n,q,a[],x,l,r,d[];
- void buildtree(int root,int l,int r){
- if (l==r) {maxx[root]=d[l]; return;}
- int mid=(l+r)>>;
- buildtree(root<<,l,mid);
- buildtree(root<<|,mid+,r);
- maxx[root]=max(abs(maxx[root<<]),abs(maxx[root<<|]));
- }
- void change(int root,int l,int r,int x,int c){
- if (l==r){
- maxx[root]+=c;
- return;
- }
- int mid=(l+r)>>;
- if (x<=mid) change(root<<,l,mid,x,c);
- if (x>mid) change(root<<|,mid+,r,x,c);
- maxx[root]=max(abs(maxx[root<<]),abs(maxx[root<<|]));
- }
- int get(int root,int l,int r,int x,int y){
- if ((x<=l)&&(y>=r)) return abs(maxx[root]);
- int ans=;
- int mid=(l+r)>>;
- if (x<=mid) ans=max(ans,get(root<<,l,mid,x,y));
- if (y>mid) ans=max(ans,get(root<<|,mid+,r,x,y));
- return ans;
- }
- int main(){
- freopen("lipschitz.in","r",stdin);
- freopen("lipschitz.out","w",stdout);
- scanf("%d",&n);
- for (int i=;i<=n;i++){
- scanf("%d",&a[i]);
- d[i]=a[i]-a[i-];
- }
- buildtree(,,n);
- scanf("%d",&q);
- while (q--){
- scanf("%d%d%d",&x,&l,&r);
- if (x==) {change(,,n,l,r-a[l]);change(,,n,l+,-r+a[l]); a[l]=r;}
- if (x==) printf("%d\n",get(,,n,l+,r));
- }
- return ;
- }
神奇的代码
数学很重要
JZOJ.5236【NOIP2017模拟8.7】利普希茨的更多相关文章
- JZOJ 5236. 【NOIP2017模拟8.7A组】利普希茨
5236. [NOIP2017模拟8.7A组]利普希茨 (File IO): input:lipschitz.in output:lipschitz.out Time Limits: 1000 ms ...
- [jzoj 5343] [NOIP2017模拟9.3A组] 健美猫 解题报告 (差分)
题目链接: http://172.16.0.132/senior/#main/show/5343 题目: 题解: 记旋转i次之后的答案为$ans_i$,分别考虑每个元素对ans数组的贡献 若$s_i& ...
- JZOJ 【NOIP2017提高A组模拟9.14】捕老鼠
JZOJ [NOIP2017提高A组模拟9.14]捕老鼠 题目 Description 为了加快社会主义现代化,建设新农村,农夫约(Farmer Jo)决定给农庄里的仓库灭灭鼠.于是,猫被农夫约派去捕 ...
- JZOJ 5246. 【NOIP2017模拟8.8A组】Trip(trip)
5246. [NOIP2017模拟8.8A组]Trip(trip) (File IO): input:trip.in output:trip.out Time Limits: 1500 ms Memo ...
- JZOJ 5235. 【NOIP2017模拟8.7A组】好的排列
5235. [NOIP2017模拟8.7A组]好的排列 (File IO): input:permutation.in output:permutation.out Time Limits: 1000 ...
- JZOJ 5230. 【NOIP2017模拟A组模拟8.5】队伍统计
5230. [NOIP2017模拟A组模拟8.5]队伍统计 (File IO): input:count.in output:count.out Time Limits: 1500 ms Memory ...
- JZOJ【NOIP2013模拟联考14】隐藏指令
JZOJ[NOIP2013模拟联考14]隐藏指令 题目 Description 在d维欧几里得空间中,指令是一个长度为2N的串.串的每一个元素为d个正交基的方向及反方向之一.例如,d = 1时(数轴) ...
- JZOJ.5281【NOIP2017模拟8.15】钦点
Description
- [jzoj 5178] [NOIP2017提高组模拟6.28] So many prefix? 解题报告(KMP+DP)
题目链接: https://jzoj.net/senior/#main/show/5178 题目: 题解: 我们定义$f[pos]$表示以位置pos为后缀的字符串对答案的贡献,答案就是$\sum_{i ...
随机推荐
- ORA-01400: 无法将 NULL 插入 ("CHARGE_WQRL"."SF_JMQTFY_T"."BH")
[ERROR] JmCheckManageDaoImpl:901 - java.sql.SQLException: ORA-01400: 无法将 NULL 插入 ("CHARGE_WQRL& ...
- JBoss类隔离
http://tiger888.iteye.com/blog/572875这几天,项目组在部署JBOSS时遇到不少问题,都是由于JBOSS的类装载问题引起,特发表一篇BLOG详细说一下JBOSS的类隔 ...
- WCF公开服务元数据方式
一般我们使用了scvutil命令自动生成了服务的客户端代理类: 例如:svcutil http://localhost:8000/?wsdl /o:FirstServiceClient.cs 命令中h ...
- Xcode中利用git源代码版本号控制
git是一个版本号控制系统,能够通过命令行来调用,也有专门的桌面软件.这里主要介绍在Xcode中怎样利用git来进行版本号的控制. 一.创建git源 从Xcode5開始引入了使用git的一些新特性.将 ...
- Atitit.减少http请求数方案
Atitit.减少http请求数方案 1. 原理与方法1 1.1. -------jsp1 1.2. "index/js.txt";2 1.3. connReduceDync2 1 ...
- 众数问题(山东理工OJ)
题目描写叙述 给定含有n个元素的多重集合S,每一个元素在S中出现的次数称为该元素的重数.多重集S中重数最大的元素称为众数. 比如,S={1,2,2,2,3.5}.多重集S的众数是2,其重数为3. 对于 ...
- 【Objective-C】03-第一个OC程序
一.打开Xcode,新建Xcode项目 二.选择最简单的命令行项目 因为我们只是学习OC语法,还未正式进入iOS开发,所以选择命令行项目即可 三.输入项目名称,选择Foundation框架进行创建项目 ...
- 通过show status 来优化MySQL数据库
1, 查看MySQL服务器配置信息 Java代码 mysql> show variables; 2, 查看MySQL服务器运行的各种状态值 Java代码 mysql> show ...
- springmvc配置AOP的两种方式
spingmvc配置AOP有两种方式,一种是利用注解的方式配置,另一种是XML配置实现. 应用注解的方式配置: 先在maven中引入AOP用到的依赖 <dependency> <gr ...
- IntelliJ IDEA Mybatis Plugin 破解安装
破解文件和截图全部在附件中,亲自破解,在使用中,感觉很棒: https://files.cnblogs.com/files/icenter/carck.zip
