论文解读（GROC）《Towards Robust Graph Contrastive Learning》

论文信息

论文标题：Towards Robust Graph Contrastive Learning
论文作者：Nikola Jovanović, Zhao Meng, Lukas Faber, Roger Wattenhofer
论文来源：2021, arXiv
论文地址：download 
论文代码：download

1 Introduction

　　创新点：从对抗攻击和对抗防御考虑数据增强策略。

2 Graph robust contrastive learning

2.1 Background

　　目的：期望同一节点在 $\tau_{1}$ 和 $\tau_{2}$ 下的嵌入是相似的。同时，期望不同节点的嵌入在两个图视图之间的嵌入是不同的。

　　令：$N e g(v)=\left\{\tau_{1}(u) \mid u \in V \backslash\{v\}\right\} \cup\left\{\tau_{2}(u) \mid u \in V \backslash\{v\}\right\}$ 是两个图视图中除 $v$ 以外的节点的嵌入。$ \sigma$ 是相似性度量函数。

　　即：

　　通过下式计算编码器的参数 $ \theta $ ：

　　　　$ \underset{\theta}{ \arg \max }  \;\;\;   \mathbb{E}_{\tau_{1}, \tau_{2} \sim \mathrm{T}}\left[\sum\limits _{v \in V} \sigma\left(z_{1}, z_{2}\right)-\sum\limits_{u \in N e g(v)} \sigma\left(z_{1}, f_{\theta}(u)\right)\right]$

　　其中 $z_{1} \equiv f_{\theta}\left(\tau_{1}(v)\right)$ ， $z_{2} \equiv f_{\theta}\left(\tau_{2}(v)\right) $

　　由于转换 $T$  的搜索空间较大，且缺乏优化算法，上述优化问题难以解决。我们遵循GRACE方法来解决这个问题。即 先对 $z_{1}, z_{2}$ 施加一个两层的 MLP ，然后再计算余弦相似度，损失函数变为：

　　　　$\frac{1}{2 n} \sum\limits _{v \in V}\left[\mathcal{L}\left(v, \tau_{1}, \tau_{2}\right)+\mathcal{L}\left(v, \tau_{2}, \tau_{1}\right)\right]\quad\quad\quad(1)$

　　其中：

　　　　$\mathcal{L}\left(v, \tau_{1}, \tau_{2}\right)=-\log {\Large \frac{\exp \left(\sigma\left(z_{1}, z_{2}\right) / t\right)}{\exp \left(\sigma\left(z_{1}, z_{2}\right) / t\right)+\sum\limits _{u \in N e g(v)} \exp \left(\sigma\left(z_{1}, f_{\theta}(u)\right) / t\right)}} $

2.2 Motivation

　　上述对比学习方法在无标签的情况下效果不错，但是其准确率在对抗攻击的条件下显著下降。

2.3 Method

对于 $ \tau_{i}^{\prime}$，我们只是使用随机特征掩蔽。对于 $\tau_{2}^{\prime}$，我们使用了两种类型的基于边缘的转换。

　　令  $\tau_{i} \in T$ 表示为数据增强组合 $ \tau_{i}=\tau_{i}^{\prime} \circ \tau_{i}^{\prime \prime} $，即随机数据增强和对抗（攻击和防御）。

普通数据增强层面：

　　分别应用随机数据增强（只用特征隐藏）$\tau_{1}^{\prime} $、 $\tau_{2}^{\prime}$ 于原始图，得到对应两个视图。

对抗层面：（边删除和边插入）

　　受对抗防御的影响，本文提出基于梯度信息选择要删除的边的策略。先对应用 $\tau^{\prime}$ 后的两个视图进行一次前向和反向传播过程，得到边缘上的梯度。因为需要最小化 $\text{Eq.1}$ ，所以选择一个最小梯度值的边子集合。

　　同时，引入基于梯度信息的边插入。由于插入所有未在图中的边不切实际，所以考虑在每个 batch $b$上处理，还将将插入集合 $S^{+}$ 限制在 边 $(u,v)$ 上。设 $ v$ 是一个锚节点，$ u$ 在 $v^{\prime} \neq v$ 的 $-hop$ 邻域内，而不在 $ v$ 的 $-hop$ 邻域内，这里暂时将 $S^{+}$ 中的边权重设置为  $1/|S^{+}|$。这里先将 $S^{+}$ 插入到两个视图。

　　然后在 Batch 中计算损失。最后分别在两个视图上进行基于梯度最小的边删除和基于最大的边插入。

　　此外，假设节点批处理还有一个额外的好处，因为这大大减少了每个 $v$ 的 $Neg(v)$ 中的负例子的数量，使个 $v$ 更多地关注它在另一个视图中的表示。GROC算法如图 1 所示，详见算法1。

　　

　　

3 Experiments

数据集及超参数设置

　　

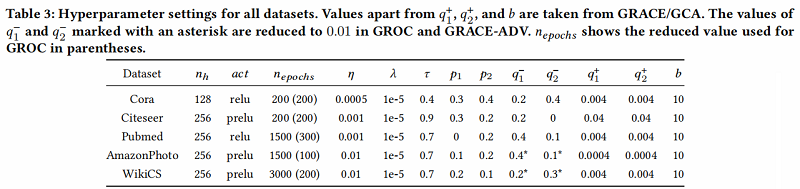
　　参数：

• • 编码器 $f_{\theta} $ 是两层的 GCN ，每层的大小分别为：$2n_h$ 、$n_h$
  • 学习率：$\eta$
  • 训练次数：$n_{epoch}$
  • L2惩罚项的惩罚因子：$\lambda$
  • 温度参数：$\tau$
  • 特征掩蔽率：$p_1$、$p_2$
  • 边删除率：$q_{1}^{-}$、$q_{2}^{-}$
  • 边插入率：$q_{1}^{+}$、$q_{2}^{+}$
  • 节点批次大小 ：$b$

基线实验

　　

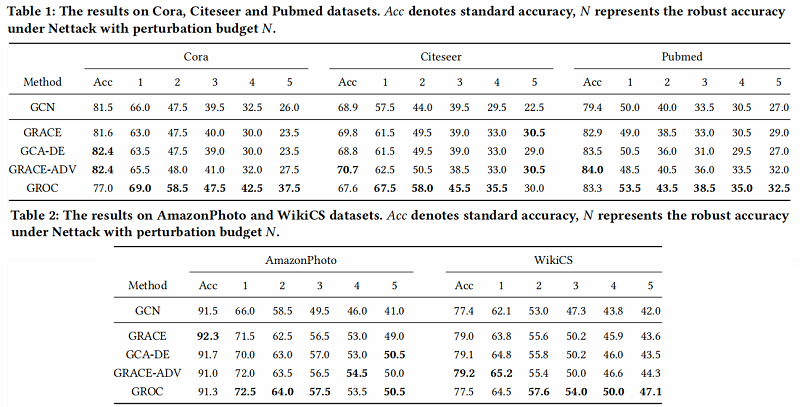
结论

　　在本研究中，我们关注图形自监督学习方法的对抗鲁棒性问题。我们怀疑，并且通过后来的实验证实，先前引入的对比学习方法很容易受到对抗性攻击。作为在这种情况下实现鲁棒性的第一步，我们引入了一种新的方法，GROC，它通过引入对抗性转换和边缘插入来增强图视图的生成。我们通过一组初步的实验证实了该方法可以提高所产生的表示的对抗性鲁棒性。我们希望这项工作最终将导致在图上产生更成功和更鲁棒的对比学习算法。

相关论文

微小扰动对高精度 GNNs 任然有影响：[7, 25, 31]
使用对抗变换是能有效提高表示能力的：[19]
基于预训练的带属性图：[12]
视觉上的对比学习：[2, 10]
图上的对比学习：[9, 27, 28, 30, 33, 36, 39, 40]
两视图（删边和属性隐藏）的对比学习：[40]
多视图图级对比学习：[36]
不需要加负样本：[8]
图上不需要加负样本：[1, 32]