【力扣】787. K 站中转内最便宜的航班加权——有向图最短路径

前言

我感觉这题比较有代表性，所以记录一下，这题是加权有向图中求最短路径的问题。

题目

787. K 站中转内最便宜的航班

动态规划

假设有一条路径是[src, i, ..., j, dst]，解法一子问题的定义是[src, i, ..., j]，解法二子问题的定义是[i, ..., j, dst]。

解法一需要知道哪些节点指向dst，需要求入度。
解法二需要知道src指向哪些节点，需要求出度。

解法一

如下图所示，想要求src到dst的最短路径，如果知道了src到s1和src到s2的最短路径，那么问题就好解决了。

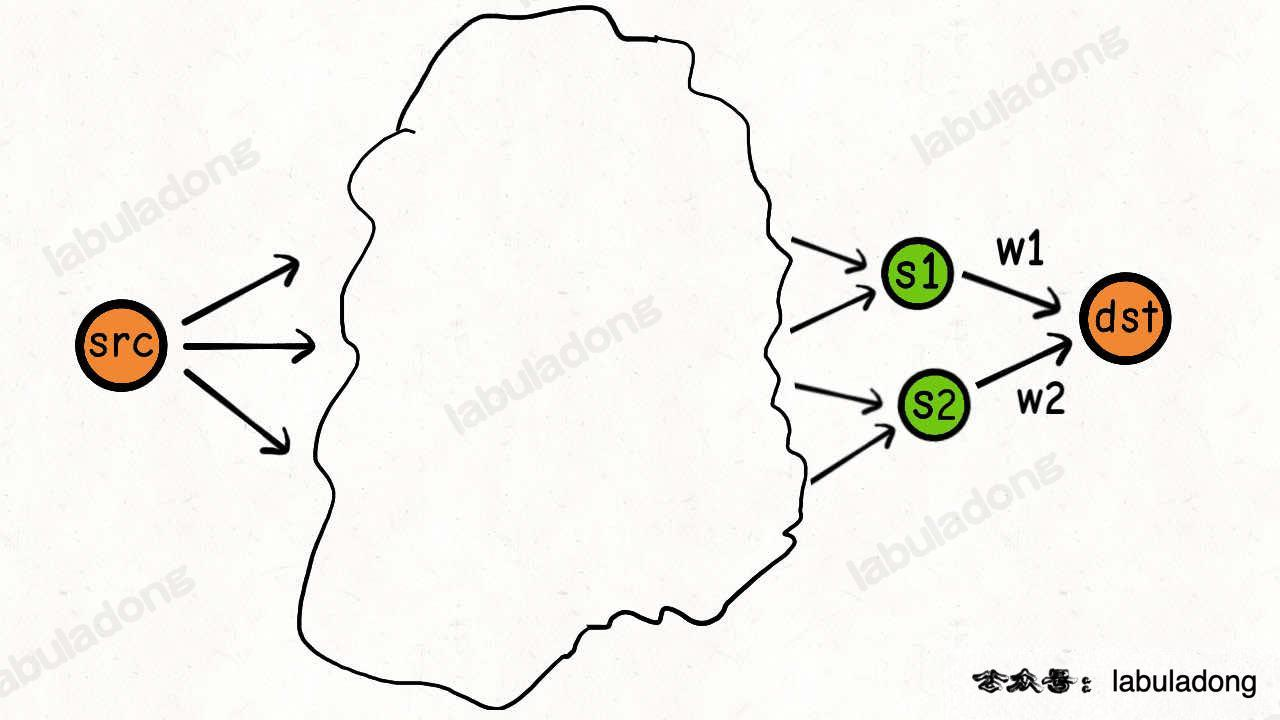
加上s1和s2到dst的花费取最小值即可，伪代码如下

minPrice(dst, k) =
	min(minPrice(s1, k - 1) + w1,
		minPrice(s2, k - 1) + w2)

最终代码

class Solution {
    int n, src, dst;
    int[][] flights;
    int[][] memo;
    HashMap<Integer, List<int[]>> indegree = new HashMap<>();

    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        this.n = n;
        this.flights = flights;
        this.src = src;
        this.dst = dst;
        // 求入度
        for(int[] flight : flights){
            int from = flight[0], to = flight[1], price = flight[2];
            indegree.putIfAbsent(to, new ArrayList<>());
            indegree.get(to).add(new int[]{from, price});
        }
        memo = new int[n][k + 1];
        for(int[] arr : memo){
            Arrays.fill(arr, -2);
        }

        return dp(dst, k);
    }

    int dp(int dst, int k){
        if(src == dst){
            return 0;
        }
        if(k < 0){
            return -1;
        }
        if(memo[dst][k] != -2){
            return memo[dst][k];
        }

        int res = Integer.MAX_VALUE;
        if(indegree.containsKey(dst)){
            for(int[] v : indegree.get(dst)){
                int subProblem = dp(v[0], k - 1);
                if(subProblem == -1) continue;
                res = Math.min(res, subProblem + v[1]);
            }
        }

        memo[dst][k] = res == Integer.MAX_VALUE ? -1 : res;
        return memo[dst][k];
    }
}

解法二

如下图所示，想要求src到dst的最短路径，如果知道了s1到dst和s2到dst的最短路径，那么问题就好解决了。

加上src到s1和s2的花费取最小值即可，伪代码如下

minPrice(src, k) =
	min(minPrice(s1, k - 1) + w1,
		minPrice(s2, k - 1) + w2)

最终代码

class Solution {
    int n, src, dst;
    int[][] flights;
    int[][] memo;
    HashMap<Integer, List<int[]>> outdegree = new HashMap<>();

    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        this.n = n;
        this.flights = flights;
        this.src = src;
        this.dst = dst;
        // 求出度
        for(int[] flight : flights){
            int from = flight[0], to = flight[1], price = flight[2];
            outdegree.putIfAbsent(from, new ArrayList<>());
            outdegree.get(from).add(new int[]{to, price});
        }
        memo = new int[n][k + 1];
        for(int[] arr : memo){
            Arrays.fill(arr, -2);
        }

        return dp(src, k);
    }

    int dp(int src, int k){
        if(src == dst){
            return 0;
        }
        if(k < 0){
            return -1;
        }
        if(memo[src][k] != -2){
            return memo[src][k];
        }

        int res = Integer.MAX_VALUE;
        if(outdegree.containsKey(src)){
            for(int[] v : outdegree.get(src)){
                int subProblem = dp(v[0], k - 1);
                if(subProblem == -1) continue;
                res = Math.min(res, subProblem + v[1]);
            }
        }

        memo[src][k] = res == Integer.MAX_VALUE ? -1 : res;
        return memo[src][k];
    }
}

小结

两种解法代码非常相似，具有对称性。对于有向图最短路径问题，常规思路都是 Dijkstra 等图论经典算法，没想到动态规划也可以，很奇妙。这也是我想记录这道题的原因吧。

BFS 算法思路

Dijkstra 算法

public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
    List<int[]>[] graph = new LinkedList[n];
    for (int i = 0; i < n; i++) {
        graph[i] = new LinkedList<>();
    }
    for (int[] edge : flights) {
        int from = edge[0];
        int to = edge[1];
        int price = edge[2];
        graph[from].add(new int[]{to, price});
    }

    // 启动 dijkstra 算法
    // 计算以 src 为起点在 k 次中转到达 dst 的最短路径
    K++;
    return dijkstra(graph, src, K, dst);
}

class State {
    // 图节点的 id
    int id;
    // 从 src 节点到当前节点的花费
    int costFromSrc;
    // 从 src 节点到当前节点经过的节点个数
    int nodeNumFromSrc;

    State(int id, int costFromSrc, int nodeNumFromSrc) {
        this.id = id;
        this.costFromSrc = costFromSrc;
        this.nodeNumFromSrc = nodeNumFromSrc;
    }
}

// 输入一个起点 src，计算从 src 到其他节点的最短距离
int dijkstra(List<int[]>[] graph, int src, int k, int dst) {
    // 定义：从起点 src 到达节点 i 的最短路径权重为 distTo[i]
    int[] distTo = new int[graph.length];
    // 定义：从起点 src 到达节点 i 的最小权重路径至少要经过 nodeNumTo[i] 个节点
    int[] nodeNumTo = new int[graph.length];
    Arrays.fill(distTo, Integer.MAX_VALUE);
    Arrays.fill(nodeNumTo, Integer.MAX_VALUE);
    // base case
    distTo[src] = 0;
    nodeNumTo[src] = 0;

    // 优先级队列，costFromSrc 较小的排在前面
    Queue<State> pq = new PriorityQueue<>((a, b) -> {
        return a.costFromSrc - b.costFromSrc;
    });
    // 从起点 src 开始进行 BFS
    pq.offer(new State(src, 0, 0));

    while (!pq.isEmpty()) {
        State curState = pq.poll();
        int curNodeID = curState.id;
        int costFromSrc = curState.costFromSrc;
        int curNodeNumFromSrc = curState.nodeNumFromSrc;

        if (curNodeID == dst) {
            // 找到最短路径
            return costFromSrc;
        }
        if (curNodeNumFromSrc == k) {
            // 中转次数耗尽
            continue;
        }

        // 将 curNode 的相邻节点装入队列
        for (int[] neighbor : graph[curNodeID]) {
            int nextNodeID = neighbor[0];
            int costToNextNode = costFromSrc + neighbor[1];
            // 中转次数消耗 1
            int nextNodeNumFromSrc = curNodeNumFromSrc + 1;

            // 更新 dp table
            if (distTo[nextNodeID] > costToNextNode) {
                distTo[nextNodeID] = costToNextNode;
                nodeNumTo[nextNodeID] = nextNodeNumFromSrc;
            }
            // 剪枝，如果中转次数更多，花费还更大，那必然不会是最短路径
            if (costToNextNode > distTo[nextNodeID]
                && nextNodeNumFromSrc > nodeNumTo[nextNodeID]) {
                continue;
            }

            pq.offer(new State(nextNodeID, costToNextNode, nextNodeNumFromSrc));
        }
    }
    return -1;
}

参考资料

旅游省钱大法：加权最短路径