P3366 模板最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz。

输入格式

第一行包含两个整数N，M，表示该图共有N个结点和M条无向边。

接下来M行每行包含三个整数 Xi，Yi，Zi，表示有一条长度为Zi​的无向边连接结点Xi，Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出orz。

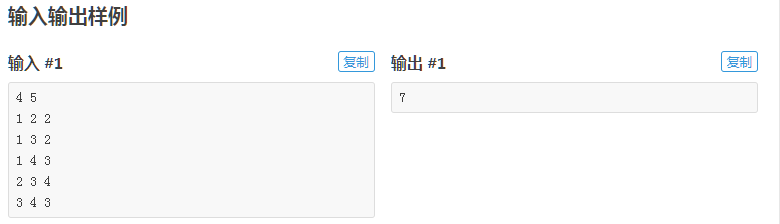
数据规模

1≤N≤5000,1≤M≤200000.

这道题是最小生成树的模板题。求最小生成树有两种算法，分别为Prim算法和Kruskal算法。在这两种算法中，Prim算法更适合于稠密图最小生成树的求解（边数远大于点数），而Kruskal算法则更适用于稀疏图的最小生成树求解（边数和点数相差不大）。最小生成树的实质就是求解一种将整张图连接起来且边权最小的问题，这里只介绍Kruskal算法，它相对于Prim算法的应用更为广泛一些。

Kruskal算法前置知识：并查集（这篇博客讲得非常清楚）。

这里直接介绍Kruskal算法的内容。

首先，Kruskal算法的成立建立在一个定理上：在一张图中，边权最小的边一定在这张图的最小生成树上。

这样我们就可以进行Kruskal算法的步骤了。

首先，我们对读入的每条边按照边权的大小从小到大进行排序。这里读入边时我们不需要开一个邻接矩阵，开一个结构体，定义三个变量来分别记录每一条边的x，y，z即可。

接下来，我们需要维护一个并查集fa[   ]，来记录这张图中的两个顶点间是否已经联通。同时，我们需要维护好并查集的两个基本操作：查(find)和并(unionn)。

然后，我们在主函数中需要枚举边，依次判断该边的两个顶点间是否已经联通，如果未联通，则将这条边加入最小生成树，同时将边权和sum加上该边的边权。

这里有一个优化：不需要枚举图中的所有边。我们记录一个变量cnt，记录一共有多少条边已被加入最小生成树。当加入的边数等于点数减一时，就可以停止循环。同时，如果我们枚举到最后一条边cnt都没有达到边数减一，说明该图本身就不连通，则建立最小生成树失败。

以上就是Kruskal算法求最小生成树的基本过程。最后奉上模板题的AC代码：

 1 #include<iostream>
 2 #include<algorithm>
 3 using namespace std;
 4 int n,m;
 5 struct bian{//开结构体来存储边
 6     int start;
 7     int end;
 8     int val;
 9 }a[200005];
10 int fa[200005];//并查集
11 bool cmp(bian a,bian b){//将边按照边权从小到大进行排序
12     return a.val<b.val;
13 }
14 int find(int x){//并查集基本操作：查询节点x的祖宗
15     if(x==fa[x]){
16         return x;
17     }else{
18         return fa[x]=find(fa[x]);//路径压缩
19     }
20 }
21 void unionn(int x,int y){//并查集基本操作：合并
22     int r1=find(x);
23     int r2=find(y);
24     fa[r1]=r2;
25 }
26 int main(){
27     cin>>n>>m;
28     for(int i=1;i<=m;i++){
29         cin>>a[i].start>>a[i].end>>a[i].val;
30     }
31     sort(a+1,a+m+1,cmp);//按照边权从小到大进行排序
32     for(int i=1;i<=n;i++){//并查集初始化
33         fa[i]=i;
34     }
35     int cnt=0;//记录已加入最小生成树的边的数量
36     int sum=0;//记录最小边权和
37     for(int i=1;i<=m;i++){
38         int x=find(a[i].start);
39         int y=find(a[i].end);
40         if(x!=y){//需要加边
41             unionn(x,y);
42             cnt++;
43             sum+=a[i].val;
44         }else{
45             continue;
46         }
47         if(cnt==n-1){//达到需要的总边数
48             break;
49         }
50     }
51     if(cnt==n-1){
52         cout<<sum<<endl;
53     }else{//建树失败
54         cout<<"orz"<<endl;
55     }
56     return 0;
57 }