回溯算法经典问题总结（.NET版）

回溯算法

回溯法其实也是一种递归，本质上就是穷举，然后筛选出符合规则的数据。为了使回溯更加高效，我们根据规则要求，在穷举过程中加上条件限制（也就是剪枝）。

我们什么场景下应该想到使用回溯法呢？

如何画图去分析问题？

如何使用代码实现呢？

如何去优化程序？

回溯算法经典问题（使用场景）

• 组合问题：N个数⾥⾯按给定规则找出k个数的集合
• 切割问题：⼀个字符串按⼀定规则有⼏种切割⽅式
• ⼦集问题：⼀个N个数的集合⾥有多少符合条件的⼦集
• 排列问题：N个数按⼀定规则全排列，有⼏种排列⽅式
• 棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序

画图分析回溯

面对回溯问题，我们第一想法就是画图！所有回溯法的问题都可以抽象为树形结构！

回溯法⼀般是在集合中递归搜索，集合的⼤⼩构成了树的宽度，递归的深度构成的树的深度。

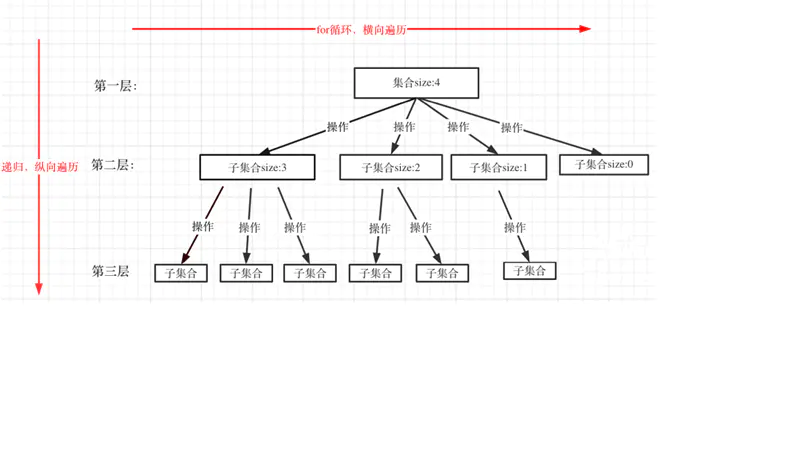
回溯法模板

public void Backtracking(参数)
{
   if(满足终止条件)
     {
          存放结果
          return;
     }
    for(遍历本层集合中的元素)
    {
        处理结点;
        dfs(参数);//递归
        撤销处理该结点; //回溯
     }
}

看下面几个例子加深理解。

组合问题

77.组合

题目：给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2

输出：

[

[2,4],

[3,4],

[2,3],

[1,2],

[1,3],

[1,4],

]

第一步：画图

我们已经知道组合是不考虑顺序的，[1,2],[2,1] 是一样的。所以我们在取数的时候，只需要取当前下标及后边下标即可。横向就是给定的n，纵向就是给定的k。按照示例n=4,k=2画出树状图如下：

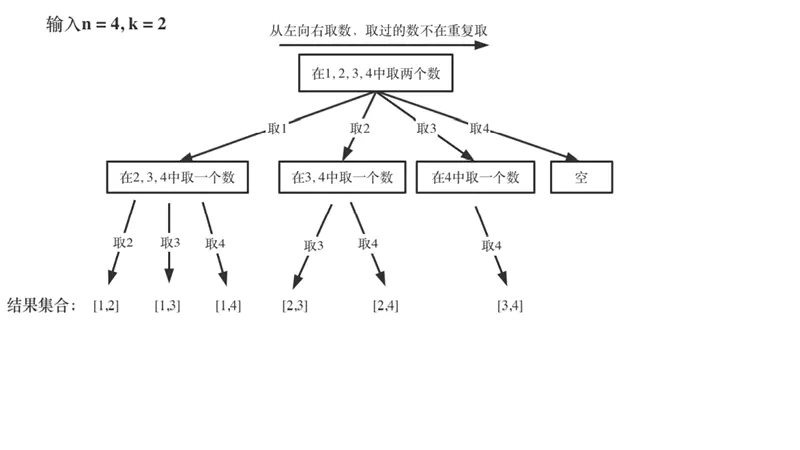
第二步：解题思路及模板的使用

//1.确定返回结果
IList<IList<int>> res = new List<IList<int>>();//存放符合条件的结果集合
List<int> path = new List<int>();//存放符合条件的结果
//2.确定入参
// * 题目给定的集合需要进入函数（此处是n,也可以是数组等集合）
// * 需要知道终结条件，本题为k
// * 题目要求返回组合，不考虑顺序，所以需要一个变量来记录当前选取n位置
//3.确定回溯方法
// startIndex用来记录本层递归的中，集合从哪里开始遍历
public void Backtracking(int n,int k,int startIndex)
{
   //4.终止条件
   if(path.Count==k)
     {
          //存放结果
          res.Add(new List<int>(path));
          return;
     }
    for(int i=startIndex;i<=n;i++)
    {
        path.Add(i);//处理节点
        Backtracking(n,i+1);//递归
        path.Remove(path.Count-1);//撤销处理该结点; 回溯
     }
}

第三步：优化剪枝

按照上边，收集叶子节点就可以写出程序了。我们如何优化程序，如何实现剪枝呢？比如n=4,k=4，按照上图所示，会进入很多次不必要的分支。我们应该剪掉。当剩余节点不能够满足条件时，就不必继续进行了。如下图所示：

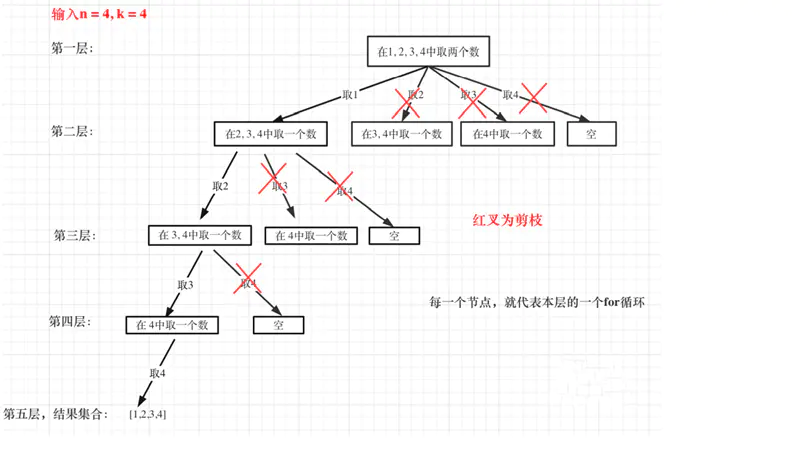
最终：完整代码

        IList<IList<int>> res = new List<IList<int>>();
        IList<int> path = new List<int>();
        public IList<IList<int>> Combine(int n, int k)
        {
            BackTracking(n, k, 1);
            return res;
        }
        public void BackTracking(int n, int k, int startIndex)
        {
            if (path.Count == k)
            {
                res.Add(new List<int>(path));
                return;
            }
            // n - (k - path.Count) + 1
            //剪枝。如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
            for (int i = startIndex; i <= n - (k - path.Count) + 1; i++)
            {
                path.Add(i);
                BackTracking(n, k, i + 1);
                path.RemoveAt(path.Count - 1);
            }
        }

40.组合总和 II

题目：给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

输入: candidates = [10,1,2,7,6,1,5], target = 8,

输出:

[

[1,1,6],

[1,2,5],

[1,7],

[2,6]

]

第一步：画图

不包含重复的组合

例如当 {candidates} = [2, 2]，{target} = 2时，上述算法会将列表 [2][2] 放入答案两次。

我们可以用一个Hash，咱.NET中使用Dictionary,将每次出现的元素和频率记录下来。不过更方便的是我们将candidates排序，查看是否和上一个元素相同。

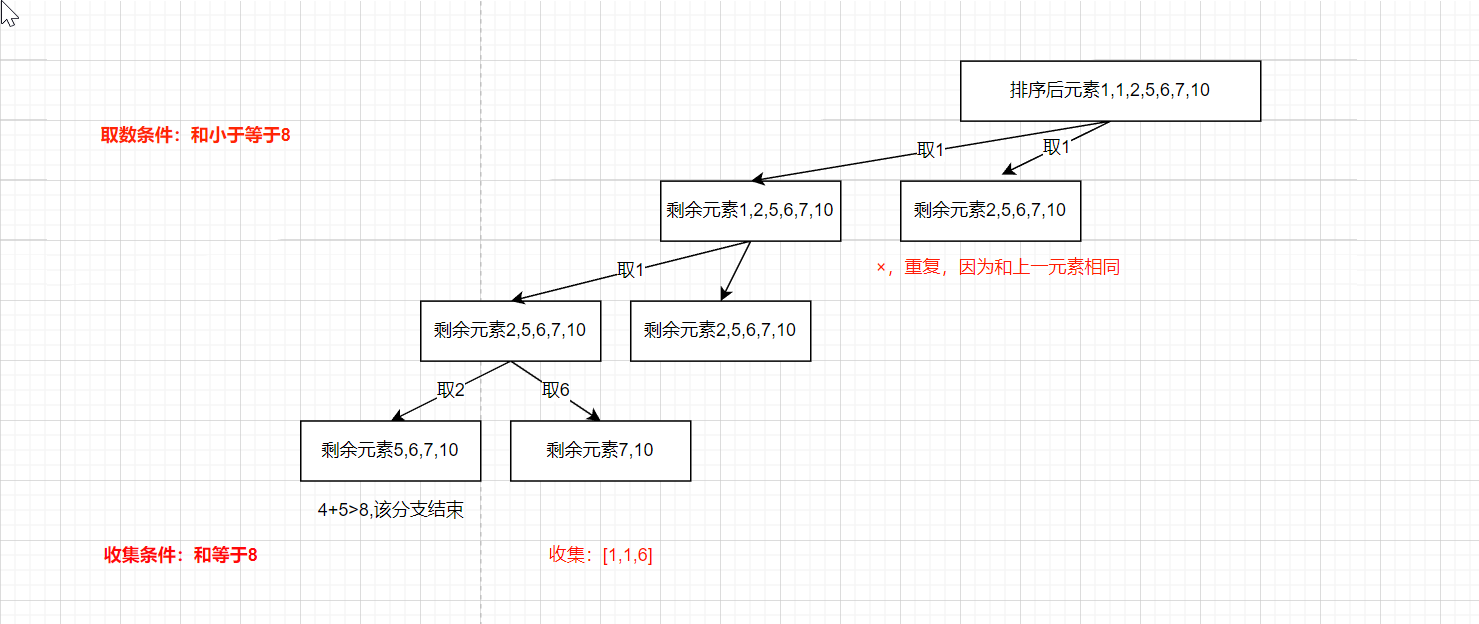
第二步：套模板

        private IList<IList<int>> result = new List<IList<int>>();//结果集
        private List<int> path = new List<int>();//结果
        int sum;
        /// <summary>
        ///
        /// </summary>
        /// <param name="candidates">元素数组</param>
        /// <param name="startIndex">开始下标</param>
        /// <param name="isUsed">记录是否使用</param>
        /// <param name="target">条件</param>
        public void BackTracking(int[] candidates, int startIndex, bool[] isUsed, int target)
        {
            if (sum == target) //终止条件
            {
                result.Add(new List<int>(path));//收集结果
                return;
            }
            for (int i = startIndex; i < candidates.Length && candidates[i] + sum <= target; i++)
            {
                //出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
                if (i > 0 && candidates[i] == candidates[i - 1] && !isUsed[i - 1])
                {
                    continue;
                }
                isUsed[i] = true;
                sum += candidates[i];
                path.Add(candidates[i]);
                //每个节点仅能选择一次，所以从下一位开始
                BackTracking(candidates, i + 1, isUsed, target);
                int temp = path[path.Count - 1];
                path.Remove(path[path.Count - 1]);
                isUsed[i] = false;
                sum -= temp;
            }

        }

第三步：剪枝优化

1. 如果选取的元素，和已经大于目标值就没必要继续进行了。

candidates[i] + sum <= target

1. 如果同层相同元素已经使用过，可以剪掉。不理解可以Debug跟一下，或者看着图想一下。

if (i > 0 && candidates[i] == candidates[i - 1] && !isUsed[i - 1])

最终：完整代码

        private IList<IList<int>> result=new List<IList<int>>();
        private IList<int> path=new List<int>();
        int sum;
        public IList<IList<int>> CombinationSum2(int[] candidates, int target)
        {
            Array.Sort(candidates);
            bool[] used = new bool[candidates.Length];
            BackTracking(candidates, 0, used, target);
            return result;
        }
        public void BackTracking(int[] candidates, int index, bool[] used, int target)
        {
            if (sum == target)
            {
                result.Add(new List<int>(path));
                return;
            }

            for (int i = index; i < candidates.Length && candidates[i]+sum<=target; i++)
            {
                //出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
                if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1])
                {
                    continue;
                }
                used[i] = true;
                sum += candidates[i];
                path.Add(candidates[i]);
                //每个节点仅能选择一次，所以从下一位开始
                BackTracking(candidates, i+1, used, target);
                int temp = path[path.Count - 1];
                path.Remove(path[path.Count-1]);
                used[i] = false;
                sum -= temp;
            }

        }

216.组合总和 III

题目：找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9

每个数字 最多使用一次 

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7

输出: [[1,2,4]]

解释:

1 + 2 + 4 = 7

第一步：画图

其实这道题和第一题差不多，就是收集结果时加了一个和的限制。

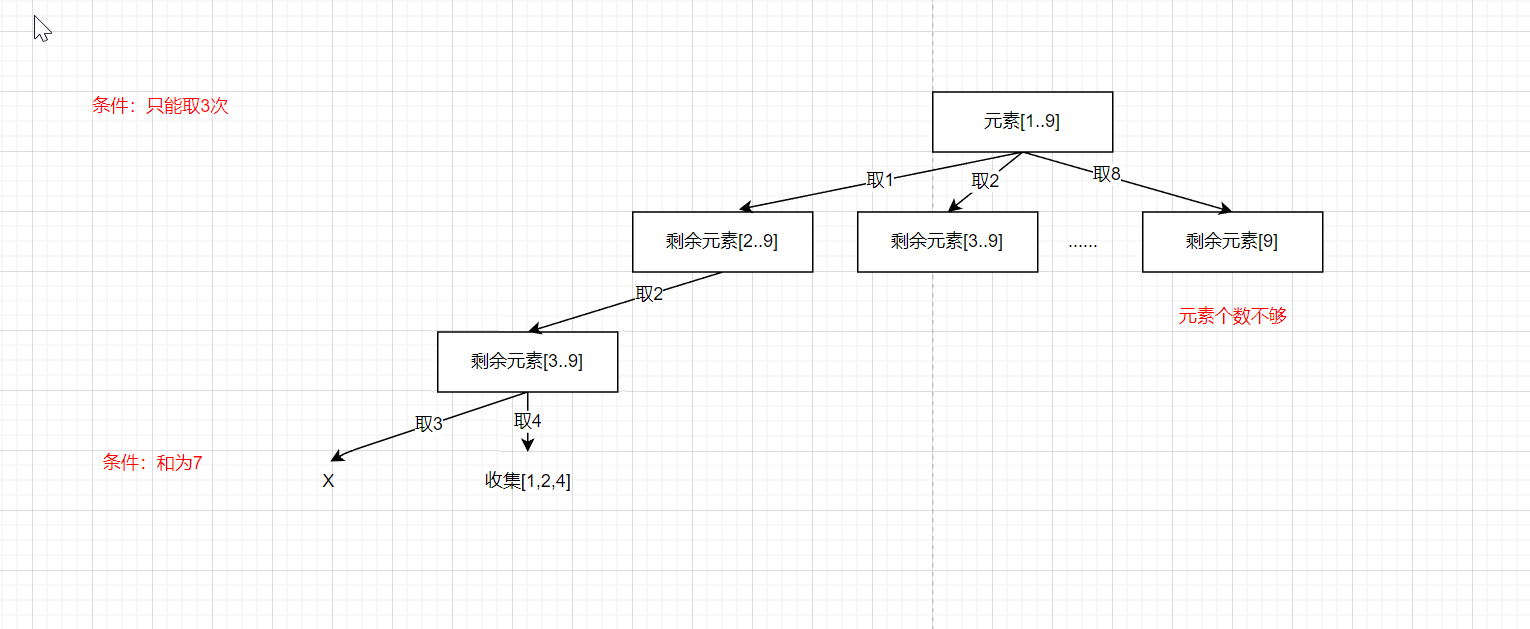
第二步：套模板

        IList<IList<int>> res = new List<IList<int>>();
        IList<int> path = new List<int>();
        /// <summary>
        ///
        /// </summary>
        /// <param name="targetSum">给定目标和</param>
        /// <param name="k">要求元素个数</param>
        /// <param name="startIndex">开始下标</param>
        /// <param name="sum">当前已选取元素和</param>
        public void BackTracking(int targetSum, int k, int startIndex, int sum)
        {
            // 减枝
            if (sum > targetSum)
            {
                return;
            }
            if (path.Count == k)
            {
                if (targetSum == sum)
                    res.Add(new List<int>(path));
                return;
            }
            // 减枝 9 - (k - path.size()) + 1
            for (int i = startIndex; i <= 9 - (k - path.Count) + 1; i++)
            {
                path.Add(i);
                sum += i;
                BackTracking(targetSum, k, i + 1, sum);
                //回溯
                path.RemoveAt(path.Count - 1);
                //回溯
                sum -= i;
            }
        }

第三步：剪枝优化

1. 选取元素小于等于目标和
2. 剩余元素个数满足条件k

最终：完整代码

        IList<IList<int>> res = new List<IList<int>>();
        IList<int> path = new List<int>();
        public IList<IList<int>> CombinationSum3(int k, int n)
        {
            BackTracking(n, k, 1, 0);
            return res;
        }
        public void BackTracking(int targetSum, int k, int startIndex, int sum)
        {
            // 减枝
            if (sum > targetSum)
            {
                return;
            }
            if (path.Count == k)
            {
                if (targetSum == sum)
                    res.Add(new List<int>(path));
                return;
            }
            // 减枝 9 - (k - path.size()) + 1
            for (int i = startIndex; i <= 9 - (k - path.Count) + 1; i++)
            {
                path.Add(i);
                sum += i;
                BackTracking(targetSum, k, i + 1, sum);
                //回溯
                path.RemoveAt(path.Count - 1);
                //回溯
                sum -= i;
            }
        }

注意点

1. 组合是无序的，所以需要strartIndex来控制选择范围，查找当前结果时，不可以再次使用。当然如果选取元素不是同一集合，就不要用startIndex了。比如17. 电话号码的字母组合

2. 题目给的元素集合，是否存在重复元素，如果存在，需要对同层相同已使用元素进行剪枝

3. 结果长度是否有要求？如果有要求判断剩余元素是否满足长度要求。

切割问题

⼦集问题

排列问题

棋盘问题

类似问题

洪水算法 flood fill

第一步：画图

第二步：套模板

第三步：剪枝优化

最终：完整代码