转载于http://blog.csdn.net/guyuealian/article/details/68487833
网上关于PCA（主成分分析）原理和分析的博客很多，本博客并不打算长篇大论推论PCA理论，而是用最精简的语言说明鄙人对PCA的理解，并在最后给出用Matlab计算PCA过程的三种方法，方便大家对PCA的理解。

源代码和附件下载地址： http://download.csdn.net/detail/guyuealian/9799160

关于PCA原理的文章，可参考：

[1] http://blog.csdn.net/guyuealian/article/details/68483384

[2] http://blog.csdn.net/guyuealian/article/details/68483213

[3] 张铮的《精通Matlab数字图像处理与识别》

一、PCA原理简要说明

PCA算法主要用于降维，就是将样本数据从高维空间投影到低维空间中，并尽可能的在低维空间中表示原始数据。PCA的几何意义可简单解释为：

0维-PCA：将所有样本信息都投影到一个点，因此无法反应样本之间的差异；要想用一个点来尽可能的表示所有样本数据，则这个点必定是样本的均值。
1维-PCA：相当于将所有样本信息向样本均值的直线投影；
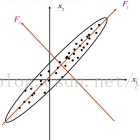
2维-PCA：将样本的平面分布看作椭圆形分布，求出椭圆形的长短轴方向，然后将样本信息投影到这两条长短轴方向上，就是二维PCA。（投影方向就是平面上椭圆的长短轴方向）；
3维-PCA：样本的平面分布看作椭圆形分布，投影方法分别是椭圆球的赤道半径a和b，以及是极半径c（沿着z轴）；

PCA简而言之就是根据输入数据的分布给输入数据重新找到更能描述这组数据的正交的坐标轴，比如下面一幅图，对于那个椭圆状的分布，最方便表示这个分布的坐标轴肯定是椭圆的长轴短轴而不是原来的x ，y轴。

那么如何求出这个长轴和短轴呢？于是线性代数就来了：我们需要先求出这堆样本数据的协方差矩阵，然后再求出这个协方差矩阵的特征值和特征向量，对应最大特征值的那个特征向量的方向就是长轴(也就是主元)的方向，次大特征值的就是第二主元的方向，以此类推。

二、PCA实现方法

实现PCA的方法，可【1】直接调用Matlab工具箱princomp( )函数实现，也可【2】自己实现PCA的过程，当然也可以【3】使用快速PCA算法的方法。

（1）方法一：[COEFF SCORE latent]=princomp(X)

参数说明：
1）COEFF 是主成分分量，即样本协方差矩阵的特征向量；
2）SCORE主成分，是样本X在低维空间的表示形式，即样本X在主成份分量COEFF上的投影，若需要降k维，则只需要取前k列主成分分量即可
3）latent：一个包含样本协方差矩阵特征值的向量；

实例：假设有8个样本，每个样本有4个特征（属性），使用PCA方法实现降维（k维，k小于特征个数4），并提取前2个主成份的特征，即将原始数据从4维空间降维到2维空间。

%% 样本矩阵X，有8个样本，每个样本有4个特征，使用PCA降维提取k个主要特征（k<4）
k=2; %将样本降到k维参数设置
X=[1 2 1 1; %样本矩阵
3 3 1 2;
3 5 4 3;
5 4 5 4;
5 6 1 5;
6 5 2 6;
8 7 1 2;
9 8 3 7]
%% 使用Matlab工具箱princomp函数实现PCA
[COEFF SCORE latent]=princomp(X)
pcaData1=SCORE(:,1:k) %取前k个主成分

%% 样本矩阵X，有8个样本，每个样本有4个特征，使用PCA降维提取k个主要特征（k<4）

k=2;                            %将样本降到k维参数设置

X=[1 2 1 1;                     %样本矩阵

      3 3 1 2;

      3 5 4 3;

      5 4 5 4;

      5 6 1 5;

      6 5 2 6;

      8 7 1 2;

      9 8 3 7]

%% 使用Matlab工具箱princomp函数实现PCA

[COEFF SCORE latent]=princomp(X)

pcaData1=SCORE(:,1:k)            %取前k个主成分

运行结果：

X =
1 2 1 1
3 3 1 2
3 5 4 3
5 4 5 4
5 6 1 5
6 5 2 6
8 7 1 2
9 8 3 7
COEFF =
0.7084 -0.2826 -0.2766 -0.5846
0.5157 -0.2114 -0.1776 0.8111
0.0894 0.7882 -0.6086 0.0153
0.4735 0.5041 0.7222 -0.0116
SCORE =
-5.7947 -0.6071 0.4140 -0.0823
-3.3886 -0.8795 0.4054 -0.4519
-1.6155 1.5665 -1.0535 1.2047
-0.1513 2.5051 -1.3157 -0.7718
0.9958 -0.5665 1.4859 0.7775
1.7515 0.6546 1.5004 -0.6144
2.2162 -3.1381 -1.6879 -0.1305
5.9867 0.4650 0.2514 0.0689
latent =
13.2151
2.9550
1.5069
0.4660
pcaData1 =
-5.7947 -0.6071
-3.3886 -0.8795
-1.6155 1.5665
-0.1513 2.5051
0.9958 -0.5665
1.7515 0.6546
2.2162 -3.1381
5.9867 0.4650

X =

     1     2     1     1

     3     3     1     2

     3     5     4     3

     5     4     5     4

     5     6     1     5

     6     5     2     6

     8     7     1     2

     9     8     3     7

COEFF =

    0.7084   -0.2826   -0.2766   -0.5846

    0.5157   -0.2114   -0.1776    0.8111

    0.0894    0.7882   -0.6086    0.0153

    0.4735    0.5041    0.7222   -0.0116

SCORE =

   -5.7947   -0.6071    0.4140   -0.0823

   -3.3886   -0.8795    0.4054   -0.4519

   -1.6155    1.5665   -1.0535    1.2047

   -0.1513    2.5051   -1.3157   -0.7718

    0.9958   -0.5665    1.4859    0.7775

    1.7515    0.6546    1.5004   -0.6144

    2.2162   -3.1381   -1.6879   -0.1305

    5.9867    0.4650    0.2514    0.0689

latent =

   13.2151

    2.9550

    1.5069

    0.4660

pcaData1 =

   -5.7947   -0.6071

   -3.3886   -0.8795

   -1.6155    1.5665

   -0.1513    2.5051

    0.9958   -0.5665

    1.7515    0.6546

    2.2162   -3.1381

    5.9867    0.4650

（2）方法二：自己编程实现

PCA的算法过程，用一句话来说，就是“将所有样本X减去样本均值m，再乘以样本的协方差矩阵C的特征向量V，即为PCA主成分分析”，其计算过程如下：
  [1].将原始数据按行组成ｍ行ｎ列样本矩阵X（每行一个样本，每列为一维特征）
  [2].求出样本X的协方差矩阵C和样本均值m；（Matlab可使用cov()函数求样本的协方差矩阵C，均值用mean函数）
  [3].求出协方差矩阵的特征值D及对应的特征向量V；（Matlab可使用eigs()函数求矩阵的特征值D和特征向量V）
  [4].将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P；（eigs()返回特征值构成的向量本身就是从大到小排序的）
  [5].Y=(X-m)×P即为降维到k维后的数据；

PS：关于协方差矩阵，很多人有点郁闷，有些教程用协方差矩阵，而有些资料是用散步矩阵计算，其实协方差矩阵和散步矩阵就是一个倍数关系：协方差矩阵C×（n-1）=散步矩阵S。我们可以使用Matlab工具箱的cov函数求协方差矩阵C。

%% 自己实现PCA的方法
[Row Col]=size(X);
covX=cov(X); %求样本的协方差矩阵（散步矩阵除以(n-1)即为协方差矩阵）
[V D]=eigs(covX); %求协方差矩阵的特征值D和特征向量V
meanX=mean(X); %样本均值m
%所有样本X减去样本均值m，再乘以协方差矩阵（散步矩阵）的特征向量V，即为样本的主成份SCORE
tempX= repmat(meanX,Row,1);
SCORE2=(X-tempX)*V %主成份：SCORE
pcaData2=SCORE2(:,1:k)

 %% 自己实现PCA的方法

[Row Col]=size(X);

covX=cov(X);                                    %求样本的协方差矩阵（散步矩阵除以(n-1)即为协方差矩阵）

[V D]=eigs(covX);                               %求协方差矩阵的特征值D和特征向量V

meanX=mean(X);                                  %样本均值m

%所有样本X减去样本均值m，再乘以协方差矩阵（散步矩阵）的特征向量V，即为样本的主成份SCORE

tempX= repmat(meanX,Row,1);

SCORE2=(X-tempX)*V                              %主成份：SCORE

pcaData2=SCORE2(:,1:k)

运行结果：

SCORE2 =
-5.7947 0.6071 -0.4140 0.0823
-3.3886 0.8795 -0.4054 0.4519
-1.6155 -1.5665 1.0535 -1.2047
-0.1513 -2.5051 1.3157 0.7718
0.9958 0.5665 -1.4859 -0.7775
1.7515 -0.6546 -1.5004 0.6144
2.2162 3.1381 1.6879 0.1305
5.9867 -0.4650 -0.2514 -0.0689
pcaData2 =
-5.7947 0.6071
-3.3886 0.8795
-1.6155 -1.5665
-0.1513 -2.5051
0.9958 0.5665
1.7515 -0.6546
2.2162 3.1381
5.9867 -0.4650

SCORE2 =

   -5.7947    0.6071   -0.4140    0.0823

   -3.3886    0.8795   -0.4054    0.4519

   -1.6155   -1.5665    1.0535   -1.2047

   -0.1513   -2.5051    1.3157    0.7718

    0.9958    0.5665   -1.4859   -0.7775

    1.7515   -0.6546   -1.5004    0.6144

    2.2162    3.1381    1.6879    0.1305

    5.9867   -0.4650   -0.2514   -0.0689

pcaData2 =

   -5.7947    0.6071

   -3.3886    0.8795

   -1.6155   -1.5665

   -0.1513   -2.5051

    0.9958    0.5665

    1.7515   -0.6546

    2.2162    3.1381

    5.9867   -0.4650

对比方法一和方法可知，主成份分量SCORE和SCORE2的绝对值是一样的（符号只是相反方向投影而已，不影响分析结果），其中pcaData是从SCORE提取前2列的数据，这pcaData就是PCA从4维降到2维空间的数据表示形式，pcaData可以理解为：通过PCA降维，每个样本可以用2个特征来表示原来4个特征了。

（3）方法三：使用快速PCA方法

PCA的计算中最主要的工作量是计算样本协方差矩阵的本征值和本征向量。假设样本矩阵X的大小为n ×d (n个d 维样本特征向量)，则样本散布矩阵(协方差矩阵) S 将是一个d×d的方阵，故当维数d较大时计算复杂度会非常高。例如当维数d=10000，S是一个10 000 ×10 000的矩阵，此时如果采用上面的princomp函数计算主成份，Matlab通常会出现内存耗尽的问题（out of memory），即使有足够多的内存，要得到S的全部本征值可能也要花费数小时的时间。

快速PCA的方法相关理论，可以参考张铮的《精通Matlab数字图像处理与识别》第12章（P307），PDF可在附件下载：http://download.csdn.net/detail/guyuealian/9799160

fastPCA函数用来对样本矩阵A进行快速主成分分析和降维(降至k维)，其输出pcaA为维后的k维样本特征向量组成的矩阵，每行一个样本，列数k为降维后的样本特征维数，相当于princomp函数中的输出SCORE，而输出V为主成分分量，相当于princomp函数中的输出COEFF。

%% 使用快速PCA算法实现的方法
[pcaData3 COEFF3] = fastPCA(X, k )

%% 使用快速PCA算法实现的方法

[pcaData3 COEFF3] = fastPCA(X, k )

其中fastPCA函数的代码实现如下：

function [pcaA V] = fastPCA( A, k )
% 快速PCA
% 输入：A --- 样本矩阵，每行为一个样本
% k --- 降维至 k 维
% 输出：pcaA --- 降维后的 k 维样本特征向量组成的矩阵，每行一个样本，列数 k 为降维后的样本特征维数
% V --- 主成分向量
[r c] = size(A);
% 样本均值
meanVec = mean(A);
% 计算协方差矩阵的转置 covMatT
Z = (A-repmat(meanVec, r, 1));
covMatT = Z * Z';
% 计算 covMatT 的前 k 个本征值和本征向量
[V D] = eigs(covMatT, k);
% 得到协方差矩阵 (covMatT)' 的本征向量
V = Z' * V;
% 本征向量归一化为单位本征向量
for i=1:k
V(:,i)=V(:,i)/norm(V(:,i));
end
% 线性变换（投影）降维至 k 维
pcaA = Z * V;
% 保存变换矩阵 V 和变换原点 meanVec

function [pcaA V] = fastPCA( A, k )

% 快速PCA

% 输入：A --- 样本矩阵，每行为一个样本

%      k --- 降维至 k 维

% 输出：pcaA --- 降维后的 k 维样本特征向量组成的矩阵，每行一个样本，列数 k 为降维后的样本特征维数

%      V --- 主成分向量

[r c] = size(A);

% 样本均值

meanVec = mean(A);

% 计算协方差矩阵的转置 covMatT

Z = (A-repmat(meanVec, r, 1));

covMatT = Z * Z';

% 计算 covMatT 的前 k 个本征值和本征向量

[V D] = eigs(covMatT, k);

% 得到协方差矩阵 (covMatT)' 的本征向量

V = Z' * V;

% 本征向量归一化为单位本征向量

for i=1:k

    V(:,i)=V(:,i)/norm(V(:,i));

end

% 线性变换（投影）降维至 k 维

pcaA = Z * V;

% 保存变换矩阵 V 和变换原点 meanVec

运行结果为：

pcaData3 =
-5.7947 -0.6071
-3.3886 -0.8795
-1.6155 1.5665
-0.1513 2.5051
0.9958 -0.5665
1.7515 0.6546
2.2162 -3.1381
5.9867 0.4650
COEFF3 =
0.7084 -0.2826
0.5157 -0.2114
0.0894 0.7882
0.4735 0.5041

[机器学习] PCA主成分分析原理分析和Matlab实现方法的更多相关文章

【建模应用】PCA主成分分析原理详解
原文载于此:http://blog.csdn.net/zhongkelee/article/details/44064401 一.PCA简介 1. 相关背景上完陈恩红老师的<机器学习与知识发现 ...
PCA(主成分分析)原理,步骤详解以及应用
主成分分析(PCA, Principal Component Analysis) 一个非监督的机器学习算法主要用于数据的降维处理通过降维,可以发现更便于人类理解的特征其他应用:数据可视化,去噪等 ...
机器学习之PCA主成分分析
前言以下内容是个人学习之后的感悟,转载请注明出处~ 简介在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性.人们自然希望变量个数较少而得到的信息较多.在很 ...
机器学习 - 算法 - PCA 主成分分析
PCA 主成分分析原理概述用途 - 降维中最常用的手段目标 - 提取最有价值的信息( 基于方差 ) 问题 - 降维后的数据的意义 ? 所需数学基础概念向量的表示基变换协方差矩阵协方差优 ...
主成分分析（PCA）原理及R语言实现
原理: 主成分分析 - stanford 主成分分析法 - 智库主成分分析(Principal Component Analysis)原理主成分分析及R语言案例 - 文库主成分分析法的原理应用及 ...
主成分分析（PCA）原理及R语言实现 | dimension reduction降维
如果你的职业定位是数据分析师/计算生物学家,那么不懂PCA.t-SNE的原理就说不过去了吧.跑通软件没什么了不起的,网上那么多教程,copy一下就会.关键是要懂其数学原理,理解算法的假设,适合解决什么 ...
PCA原理分析
动机在机器学习领域中,我们常常会遇到维数很高的数据,有些数据的特征维度高达上百万维,很显然这样的数据是无法直接计算的,而且维度这么高,其中包含的信息一定有冗余,这时就需要进行降维,总的来说,我们降维 ...
opencv——PCA（主要成分分析）数学原理推导
引言: 最近一直在学习主成分分析(PCA),所以想把最近学的一点知识整理一下,如果有不对的还请大家帮忙指正,共同学习. 首先我们知道当数据维度太大时,我们通常需要进行降维处理,降维处理的方式有很多种, ...
[机器学习]-PCA数据降维：从代码到原理的深入解析
&*&:2017/6/16update,最近几天发现阅读这篇文章的朋友比较多,自己阅读发现,部分内容出现了问题,进行了更新. 一.什么是PCA:摘用一下百度百科的解释 PCA(Prin ...
PCA主成分分析 ICA独立成分分析 LDA线性判别分析 SVD性质
机器学习(8) -- 降维核心思想:将数据沿方差最大方向投影,数据更易于区分简而言之:PCA算法其表现形式是降维,同时也是一种特征融合算法. 对于正交属性空间(对2维空间即为直角坐标系)中的样本点 ...

随机推荐

LeNet-论文阅读
概述 Yann LeCun, Leon Bottou, Yoshua Bengio, and Patrick Haffner的论文<Gradient-Based Learning Applied ...
hmtl5 web SQL 和indexDB
前端缓存有cookie,localStorage,sessionStorage,webSQL,indexDB: cookie:有缺点 localStorage:功能单一 sessionStorage: ...
【SDOI2013】项链题解
Solution 将原问题分为两个问题求解. Part 1 首先求珍珠的种类数. 设\(f_i\)表示满足\(gcd = i\)的本质不同珍珠个数, \(g_i\)表示满足\(gcd\)为\(i\)的 ...
小白转行入门STM32----手机蓝牙控制STM32单片机点亮LED
@ 目录引言导读一.通信基础知识 1.1 通信到底传输的是什么? 1.2 比特率和波特率习题 1.1 双工和单工习题 1.2 串行和并行 1.3 异同通信和同步通信习题二.连接STM32单 ...
Vue 中为什么要有nextTick？
摘要:本文将浅析nextTick的作用.使用场景和背后的原理实现,希望对大家有所帮助. 本文分享自华为云社区<Vue 中的 nextTick 有什么作用?>,作者:CoderBin. 一. ...
题解 UVA10285 最长的滑雪路径 Longest Run on a Snowboard
Solution 双倍经验就是记搜嘛. 搞一个二维数组记录一下当前的最长滑雪路径,其他和普通 dfs 没什么两样. 向 \(4\) 个方向搜索,如果高度符合就 \(+1\) . 多测要注意数组初始化 ...
JS逆向实战7-- 某省在线审批网站params 随机生成
参数分析我们首先通过抓包发现这个就是我们所需要的数据然后我们通过fidder 发起请求结果: 通过我们反复测试发现这个params的参数是每次请求中都会变化的断点查找我们通过这个t参数 ...
从 QFramework 重新开始
自从上一篇博文写完后,就进入了繁忙工作状态,直到最近才开始有一点空闲时间. 这次繁忙的状态从 2022 年 10 月 11 日持续到 2022 年 11 月 5 日. 主要的工作就是 QFramew ...
c++ 关于引用变量你不知道的东西
引用变量延迟绑定我们知道引用变量定义时要立刻赋值,告诉编译器他是谁的引用.如果不赋值,编译会失败. 如果引用变量是单个定义的,对他赋值还比较简单. struct test_T { int data; ...
孙荣辛｜大数据穿针引线进阶必看——Google经典大数据知识
大数据技术的发展是一个非常典型的技术工程的发展过程,荣辛通过对于谷歌经典论文的盘点,希望可以帮助工程师们看到技术的探索.选择过程,以及最终历史告诉我们什么是正确的选择. 何为大数据 "大 ...

[机器学习] PCA主成分分析原理分析和Matlab实现方法