吴恩达老师机器学习课程chapter01——序言+回归

吴恩达老师机器学习课程01——序言+线性回归

本文是非计算机专业新手的自学笔记，欢迎指正与其他任何合理交流。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第一章、第二章、第四章。

---

目录

• 吴恩达老师机器学习课程01——序言+线性回归
  • 序言
  • 最简单的线性回归（单特征）
    • 基本概念
    • 代价函数
    • 利用梯度下降解最优问题
  • 多特征线性回归
    • 利用梯度下降解优化问题
    • 直接求导/正规方程法
    • 几点注意

---

序言

机器学习中两种最基本的类别：

- 监督学习(Supervised learning)
	- 回归(Regression)
	- 分类(Classification)
- 无监督学习(Unsupervised learning)
	- 聚类(Cluster)

---

最简单的线性回归（单特征）

基本概念

例题如下：

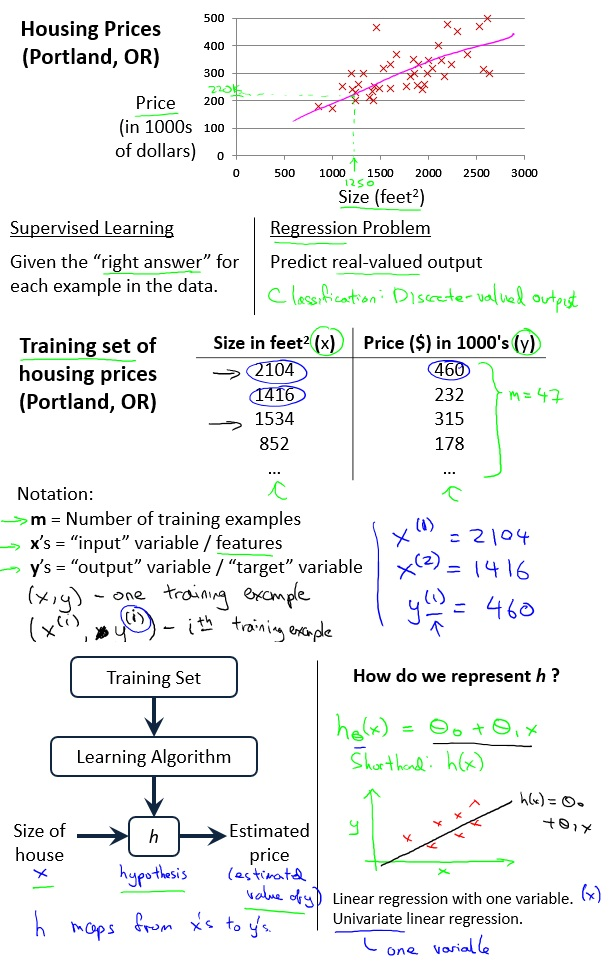
m：训练集中样本数量；

i：样本序号；

x：输入；

y：输出；

θ：为待定参数组成的向量，一般记成列向量。

单特征（x为一维向量）线性规划中：

\[h_{\theta} (x ) = \theta _{0} x_{0}+\theta _{1} x_{1}
\]

其中x0=1，可以用\(\theta _{0} x_{0}\)表示常数。

问题：如何确定θ？

代价函数

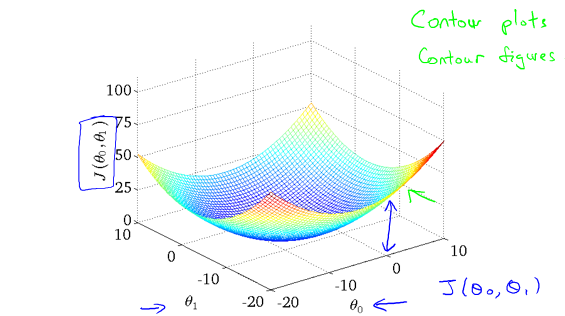
定义代价函数\(J(θ)\)：

\[J(θ)=\frac{1}{2m} \sum_{i=1}^{m} \left ( h_{\theta} (x^{(i)} ) -y^{(i)} \right ) ^2
\]

不同的θ会导致\(J(θ)\)大小变化。

例如：

(1)

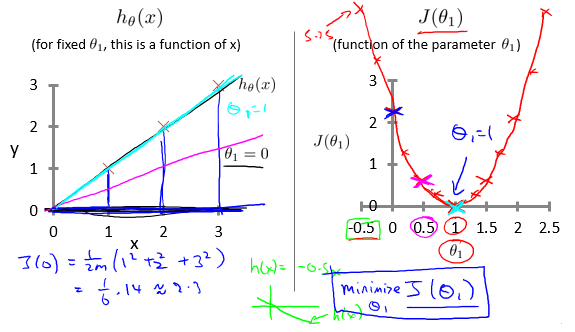
(2)

认为\(J(θ)\)越小，拟合效果越好。

故问题转化为优化问题如下：

利用梯度下降解最优问题

此处不推导梯度下降法，直接使用。

这里使用的梯度下降法，为Batch Gradient Descent，即每一步下降使用了所有训练样本。

利用梯度下降法解该最优问题的表达式如下：

\[\theta _{j} = \theta _{j} -\alpha \frac{\partial }{\partial \theta _{j}}J\left (\theta \right )
\]

其中，α表示步长，机器学习中称之为学习率(learning rate)。

学习率的选取很重要：过大会导致发散，无法收敛；过小会导致算法步数过多，花费时间长。吴恩达老师建议，可以如“0.03，0.1，0.3,1……”这样取值。

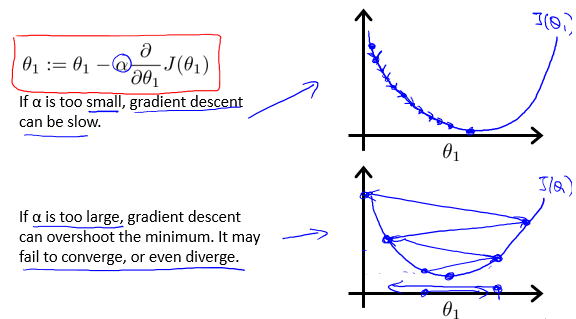
梯度下降法在编程时应当注意同步更新θ：

多特征线性回归

特征的向量x不再是一维向量。

例题如下：

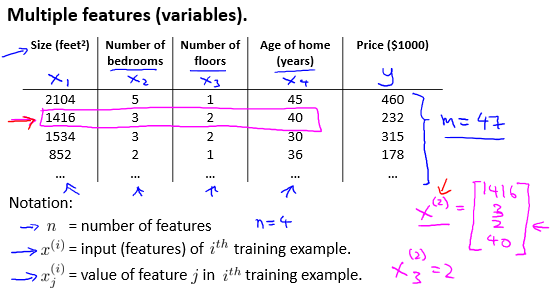
因此要做出以下改变：

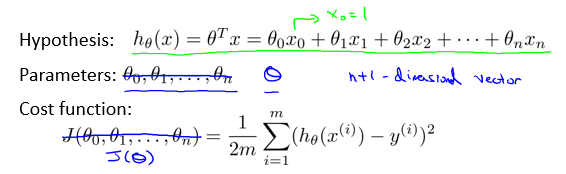
利用梯度下降解优化问题

直接求导/正规方程法

正规方程方法的推导如下（不包含矩阵与向量求导的推导）：

几点注意

• 特征的缩放(Feature Scaling)
  
  特征的数量级差别过大会导致梯度下降步数过多。可以通过$x=\frac{x-\mu }{max(x_{i} )-min(x_{i} )} $的方法进行规格化。
  
  正规方程法中就不需要了。
• 多项式回归(Polynomial Regression)
  
  可以将x、x^2、x^3……视为不同特征，进行多特征拟合，得到多项式回归结果，进行非线性拟合。
• 正规方程中不可求逆
  
  求逆(inv)时，出现矩阵不可逆很可能是因为特征出现冗余，不同特征之间线性相关。可以删除部分特征。无法删除时可以求其伪逆(pinv)。
• 正规方程法很直接，但是在n很大时，求矩阵乘法和逆的过程运算会变慢。