20160730noip模拟赛zld

codeforces394E

如果没有在凸多边形内一点的限制，答案肯定是

如果不在凸多边形内，那么目标点肯定在凸多边形边上，我们枚举每条边，在每条边上求出距离平方和最小的点，在这些点中求出最小的

我们可以发现固定一点计算这个平方和不要O(m)的时间，只要维护x坐标平方和，x坐标的和就可以O(1)计算，但是计算起来很鬼畜

其实最后答案就是凸多边形上，离这个最近的点。

#include<map>
#include<stack>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<complex>
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;
#define inf 1001001001
#define infll 1001001001001001001LL
#define FOR0(i,n) for(int (i)=0;(i)<(n);++(i))
#define FOR1(i,n) for(int (i)=1;(i)<=(n);++(i))
#define ll long long
#define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl
#define gmax(a,b) (a)=max((a),(b))
#define gmin(a,b) (a)=min((a),(b))
#define ios0 ios_base::sync_with_stdio(0)
#define Ri register int
#define gc getchar()
#define il inline
il int read(){
    bool f=true;
    Ri x=0;char ch;
    while(!isdigit(ch=gc))if(ch=='-')f=false;
    while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}
    return f?x:-x;
}
#define gi read()
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
int n,m;
#define eps 1e-6
struct point{
    double x,y;
    il void rd(){
        x=gi;y=gi;
    }
    point operator+(point a) {return (point){x+a.x,y+a.y};}
    point operator-(point a) {return (point){x-a.x,y-a.y};}
    point operator*(double a){return (point){x*a,y*a};}
    point operator/(double a){return (point){x/a,y/a};}
    double operator^(point a){return x*a.y-y*a.x;}//叉积
    double operator&(point a){return x*a.x+y*a.y;}//点积
}p[100001],q[100001];
//q m个点的 多边形
//p n个目标点
double A,B,C;
bool inside(point a,point b,point c){//chk if a between b-c
    double A=a-b&c-b;
    double B=c-b&c-b;
    double C=a-b^c-b;
    if (fabs(C)>eps) return 0;
    if (A>-eps&&A<B+eps) return 1;
    return 0;
}
int in_hull(point *b,point q) {
    int cnt=0;
    FOR1(i,m){
        if(inside(q,b[i],b[i+1]))    return 2;
        if((b[i]-q^b[i+1]-q)>eps)    cnt++;
    }
    if (cnt==m||!cnt) return 1;
    return 0;
}
double dist(point a,point b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int main(){
    FO(point);
    n=gi;
    FOR1(i,n)p[i].rd();
    m=gi;
    FOR1(i,m)q[i].rd();q[0]=q[m];
    double sx,sy,sx2,sy2;sx=sy=sx2=sy2=0;
    FOR1(i,n)sx+=p[i].x,sy+=p[i].y,sx2+=p[i].x*p[i].x,sy2+=p[i].y*p[i].y ;
    if(in_hull(q,(point){sx/n,sy/n})){
        double ans=0.0;
        FOR1(i,n)ans+=dist((point){sx/n,sy/n},p[i]);
        printf("%.8lf",ans);
        //做到这里发现不会算不在多边形内的
    }else{
        sx*=2.0;sy*=2.0;
        double ans=infll;
        for(int i=0;i<m;i++){
            int s=i,t=i+1;
            double dx=q[t].x-q[s].x,dy=q[t].y-q[s].y;
            double a=q[s].x,b=q[s].y;
            double A=dx*dx+dy*dy,B=2*a*dx+2*b*dy-sx/n*dx-sy/n*dy;
            double k=(-B)/(2*A);
            if(k<0) k=0;
            if(k>1) k=1;
            double x=a+dx*k,y=b+dy*k;
            double ss=n*(x-sx/(2.0*n))*(x-sx/(2.0*n))+sx2-(sx*sx)/(4.0*n)+n*(y-sy/(2.0*n))*(y-sy/(2.0*n))+sy2-(sy*sy)/(4.0*n);
            ans=min(ans,ss);
        }
        printf("%.8lf\n",ans);
    }
    //30/07/16 09:38如果WA了就是哪里nm pq反了
    //30/07/16 09:52写完发现推的不对
    //
    return 0;
}

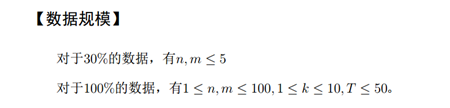
套用一位大佬的话，这是一道送命题

题目要求相当于是使每一行都与第一行相等或者完全相反

那么就大概有了思路

当n>k时。肯定有没被修改的行，我们枚举这个行在哪

当n<=k时，枚举第一列的状态，统计答案

#include<stack>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<complex>
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;
#define inf 1001001001
#define infll 1001001001001001001LL
#define FOR0(i,n) for(int (i)=0;(i)<(n);++(i))
#define FOR1(i,n) for(int (i)=1;(i)<=(n);++(i))
#define ll long long
#define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl
#define gmax(a,b) (a)=max((a),(b))
#define gmin(a,b) (a)=min((a),(b))
#define ios0 ios_base::sync_with_stdio(0)
#define Ri register int
#define gc getchar()
#define il inline
il int read(){
    bool f=true;
    Ri x=0;char ch;
    while(!isdigit(ch=gc))if(ch=='-')f=false;
    while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}
    return f?x:-x;
}
#define gi read()
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
int n,m,k,map[101][101];

int main(){
    FO(table);
    int T=gi;
    while(T--){
        n=gi;m=gi;k=gi;
        FOR1(i,n)FOR1(j,m)map[i][j]=gi;
        if(n>k){
            int res=inf,ans;
            FOR1(i,n){
                ans=0;
                FOR1(j,n){
                    int cnt=0;
                    if(i!=j)
                        FOR1(k,m){
                            cnt+=map[i][k]^map[j][k];
                        }
                    ans+=min(cnt,m-cnt);
                }
                gmin(res,ans);
            }
            printf("%d\n",res>k?-1:res);
        }else{
            bool p[101];int ans=inf;
            FOR0(st,1<<n){
                FOR1(i,n)p[i]=st&(1<<(i-1));
//                FOR1(i,n)cout<<p[i];puts("");
                int res=0;
                FOR1(i,n)res+=(p[i]^map[i][1]);
                FOR1(i,m){
                    int cnt=0;
                    FOR1(j,n)cnt+=(p[j]^map[j][i]);
                    res+=min(cnt,n-cnt);
                }
//                cout<<res<<endl;
                gmin(ans,res);
            }
            printf("%d\n",ans>k?-1:ans);
        }
//        puts("----------------------------");
    }
    return 0;
}

T3

还没做