Spark 2.0 PCA主成份分析

PCA在Spark2.0中用法比较简单，只需要设置：

.setInputCol(“features”)//保证输入是特征值向量
.setOutputCol(“pcaFeatures”)//输出
.setK()//主成分个数 

注意：PCA前一定要对特征向量进行规范化（标准化）！！！

//Spark 2.0 PCA主成分分析
//注意：PCA降维前必须对原始数据（特征向量）进行标准化处理
package my.spark.ml.practice;

import org.apache.spark.ml.feature.PCA;
import org.apache.spark.ml.feature.PCAModel;//不是mllib
import org.apache.spark.ml.feature.StandardScaler;
import org.apache.spark.sql.Dataset;
import org.apache.spark.sql.Row;
import org.apache.spark.sql.SparkSession;

public class myPCA {

    public static void main(String[] args) {
        SparkSession spark=SparkSession
                .builder()
                .appName("myLR")
                .master("local[4]")
                .getOrCreate();
        Dataset<Row> rawDataFrame=spark.read().format("libsvm")
          .load("/home/hadoop/spark/spark-2.0.0-bin-hadoop2.6" +
                "/data/mllib/sample_libsvm_data.txt");
        //首先对特征向量进行标准化
        Dataset<Row> scaledDataFrame=new StandardScaler()
                  .setInputCol("features")
                  .setOutputCol("scaledFeatures")
                  .setWithMean(false)//对于稀疏数据（如本次使用的数据），不要使用平均值
                  .setWithStd(true)
                  .fit(rawDataFrame)
                  .transform(rawDataFrame);
        //PCA Model
        PCAModel pcaModel=new PCA()
                      .setInputCol("scaledFeatures")
                      .setOutputCol("pcaFeatures")
                      .setK()//
                      .fit(scaledDataFrame);
        //进行PCA降维
        pcaModel.transform(scaledDataFrame).select("label","pcaFeatures").show(,false);
    }
}

/**
 * 没有标准化特征向量，直接进行PCA主成分：各主成分之间值变化太大，有数量级的差别。
+-----+------------------------------------------------------------+
|label|pcaFeatures                                                 |
+-----+------------------------------------------------------------+
|0.0  |[-1730.496937303442,6.811910953794295,2.8044962135250024]   |
|1.0  |[290.7950975587044,21.14756134360174,0.7002807351637692]    |
|1.0  |[149.4029441007031,-13.733854376555671,9.844080682283838]   |
|1.0  |[200.47507801105797,18.739201694569232,22.061802015132024]  |
|1.0  |[236.57576401934855,36.32142445435475,56.49778957910826]    |
|0.0  |[-1720.2537550195714,25.318146742090196,2.8289957152580136] |
|1.0  |[285.94940382351075,-6.729431266185428,-33.69780131162192]  |
|1.0  |[-323.70613777909136,2.72250162998038,-0.528081577573507]   |
|0.0  |[-1150.8358810584655,5.438673892459839,3.3725913786301804]  |
 */
/**
 * 标准化特征向量后PCA主成分，各主成分之间值基本上在同一水平上，结果更合理
 |label|pcaFeatures                                                  |
+-----+-------------------------------------------------------------+
|0.0  |[-14.998868464839624,-10.137788261664621,-3.042873539670117] |
|1.0  |[2.1965800525589754,-4.139257418439533,-11.386135042845101]  |
|1.0  |[1.0254645688925883,-0.8905813756164163,7.168759904518129]   |
|1.0  |[1.5069317554093433,-0.7289177578028571,5.23152743564543]    |
|1.0  |[1.6938250375084654,-0.4350617717494331,4.770263568537382]   |
|0.0  |[-15.870371979062549,-9.999445137658528,-6.521920373215663]  |
|1.0  |[3.023279951602481,-4.102323190311296,-9.451729897327345]    |
|1.0  |[3.500670997961283,-4.1791886802435805,-9.306353932746568]   |
|0.0  |[-15.323114679599747,-16.83241059234951,2.0282183995400374]  |
*/

如何选择k值？

//PCA Model
        PCAModel pcaModel=new PCA()
                      .setInputCol("scaledFeatures")
                      .setOutputCol("pcaFeatures")
                      .setK()//
                      .fit(scaledDataFrame);
        int i=;
        for(double x:pcaModel.explainedVariance().toArray()){
        System.out.println(i+"\t"+x+"  ");
        i++;
        }
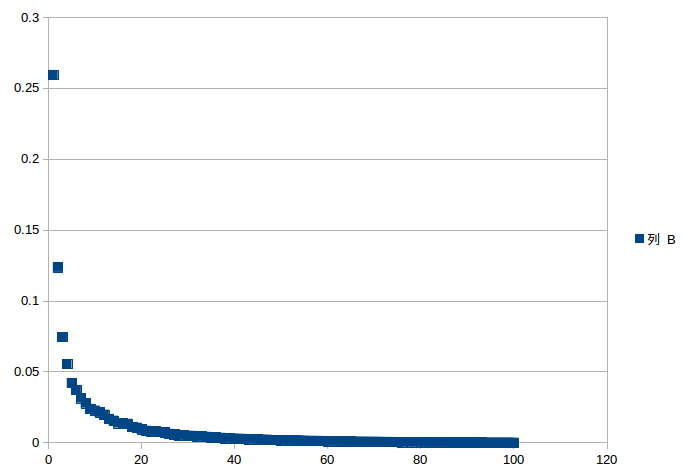
输出100个降序的explainedVariance（和scikit-learn中PCA一样）：
   0.25934799275530857
   0.12355355301486977
   0.07447670060988294
   0.0554545717486928
   0.04207050513264405
   0.03715986573644129
   0.031350566055423544
   0.027797304129489515
   0.023825873477496748
  0.02268054946233242
  0.021320060154167115
  0.019764029918116235
  0.016789082901450734
  0.015502412597350008
  0.01378190652256973
  0.013539546429755526
  0.013283518226716669
  0.01110412833334044
...

大约选择20个主成分就足够了 
随便做一个图可以选择了（详细可参考Scikit-learn例子） 
http://scikit-learn.org/stable/auto_examples/plot_digits_pipe.html