OO第一单元总结__多项式求导问题

---

作业一、含幂函数的简单多项式的求导

（1）基于度量的程序结构分析

1. 统计信息图：

2. 结构信息图：

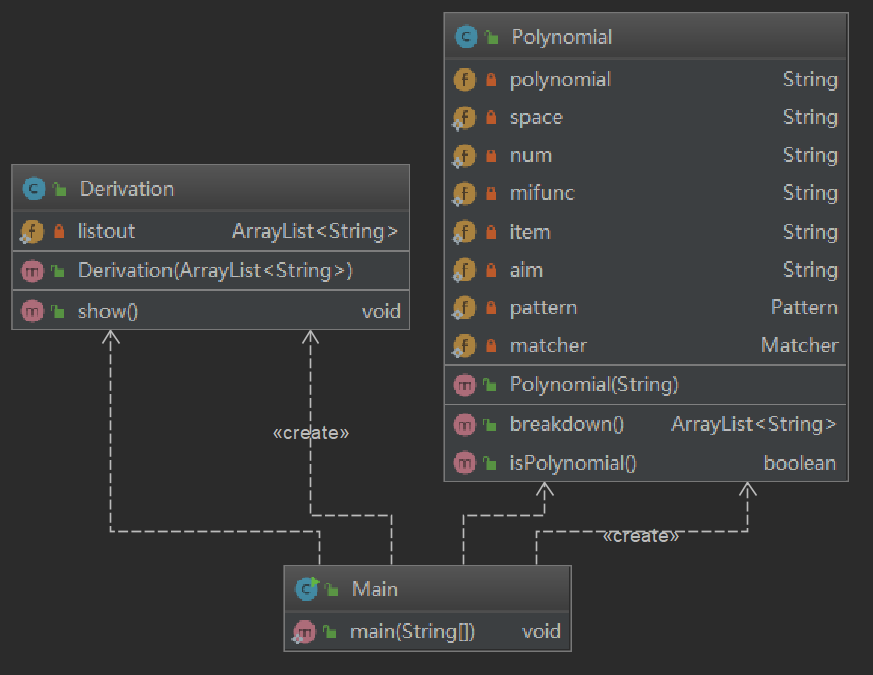
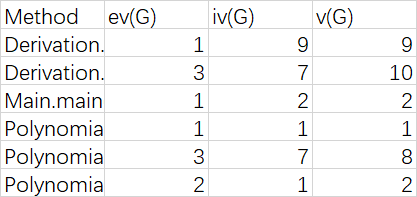
3. 复杂度分析

　　基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

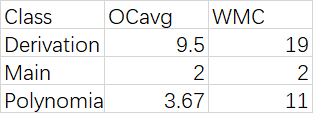
　　OCavg为平均循环复杂度;WMC为总循环复杂度

4. 分析：

本次作业一共使用3个类，没有使用继承、接口。

Main类：

　　1）程序入口

　　2）主要业务逻辑层

　　3）处理输入String

Polynomial类：处理多项式

　　1）正则表达式判WF（大正则）

　　2）简化输入String

　　3）分解成单项式：

　　　　用ArrayList<String>储存

　　3）组合单项式的输出String：

　　　　最终将ArrayList<String>转为String

　　4）简化输出String

Deviation类：单项式求导

　　1）求导

　　2）生成输出String

（2）程序BUG分析

1. 强测中未被查出BUG，但由于-1*cos(x)未被简化成-cos(x)，被扣了性能分。

输入	我的输出	原因
-sin(x)	-1*cos(x)	在优化时只优化了+1*x-->+x,忘记了-1的情况，并且测试也不全面

2. 互测中未被查出BUG

（3）程序测试分析

1. 本次作业同学们的BUG集中在WF方面，/f，/v，+，**，末尾加空格等情况可能没有判出WF（BUG类似，不一一列举）。

2. 个人觉得一个有效解决非法字符的办法是先将正确字符从输入表达式中删除，再判断输入是否为空，不为空则WF。

3. 本次测试方法是构造各种WF的数据。

---

作业二、含三角函数的普通多项式的求导

（1）基于度量的程序分析

1. 统计信息图：

2. 结构信息图：

3. 复杂度分析

　　基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

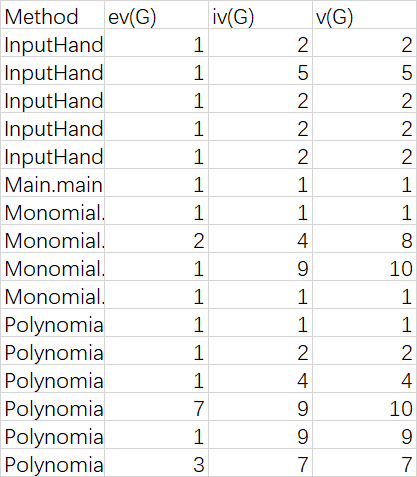
　　OCavg为平均循环复杂度;WMC为总循环复杂度

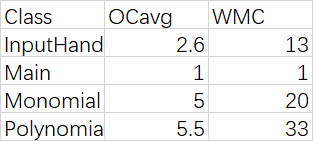
4. 分析：

本次作业一共使用4个类，没有使用继承、接口。

Main类：

　　1）程序入口

　　2）主要业务逻辑层

InputHandler类：

　　1）处理输入String

　　2）少部分判WF

　　3）简化输入String

Polynomial类：处理多项式

　　1）大部分判WF（大正则）

　　2）分解成单项式：

　　　　用ArrayList<String>储存

　　3）组合单项式的输出String：

　　　　最终将ArrayList<String>转为String

　　4）简化输出String：

　　　　合并同类项，去0项，去1*，去-1*，找到正项做首项并去掉+， cos(x)^2+sin(x)^2 合并（任意系数的可合并项）

Monomial类：处理单项式

　　1）合并同类项

　　　　合并后形如 a*x^b*sin(x)*c*cos(x)^d

　　2）求导：

　　　　对于一个单项式，设其为a*x^b*sin(x)*c*cos(x)^d，再设其导数为A1*x^B1*sin(x)*C1*cos(x)^D1 + A2*x^B2*sin(x)*C2*cos(x)^D2 + A3*x^B3*sin(x)*C3*cos(x)^D3，通过数学运算可求出各参数值。

　　3）生成输出String

（2）程序BUG分析

1.  强测中未被查出BUG，但由于只做了一部分优化，被扣了性能分。

　　e.g.　　 sin(x)^3*cos(x)+sin(x)*cos(x)^3 可化简为--> sin(x)*cos(x) ，但是这种化简比较复杂，我为了保证正确没有实现。

2. 互测中未被查出BUG

（3）程序测试分析

　　 测试方法：我用之前构造的测试样例先大致测试一遍，在观察一些易考察的部分（如：正则表达式），进行针对性测试。

　　本次debug情况如下：

输入	输出	原因
sin(x) * sin(x) * cos(x) ^-2 *x	WRONG FORMAT！	无法识别多个三角函数连乘

---

作业三、支持嵌套的复杂多项式的求导

（1）基于度量的程序分析

1. 统计信息图：

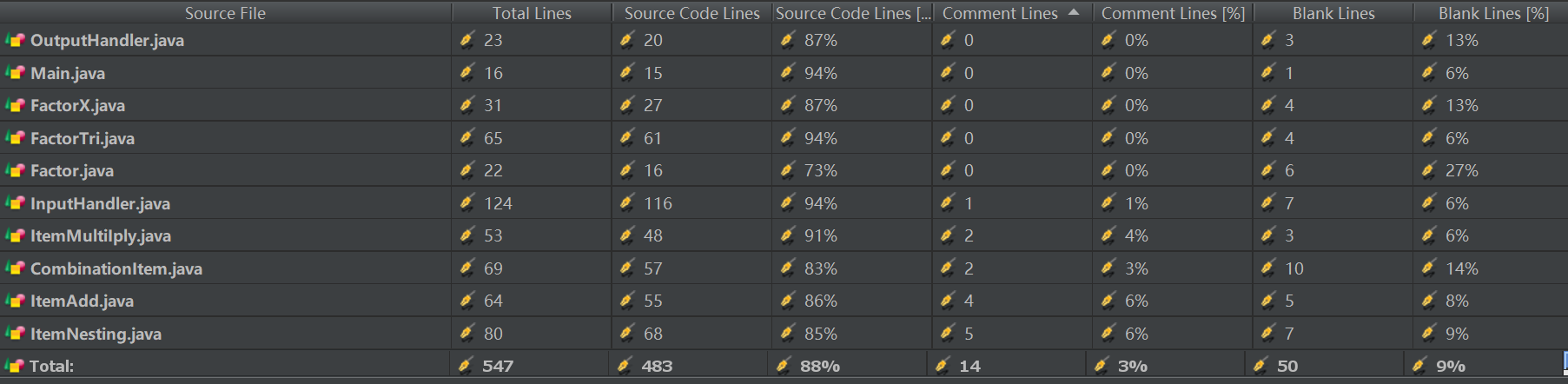
2. 结构信息图：

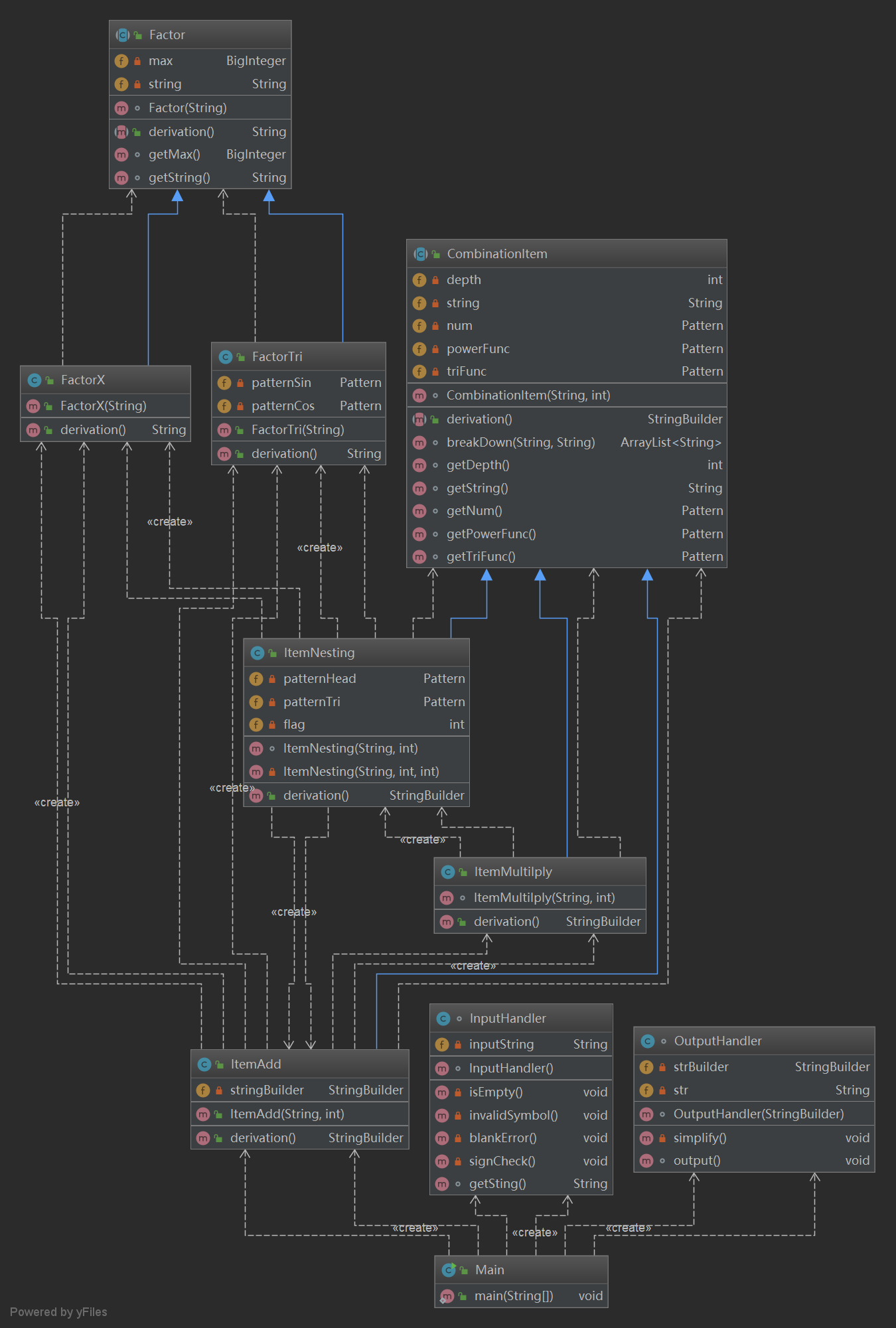
3. 复杂度分析

　　基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

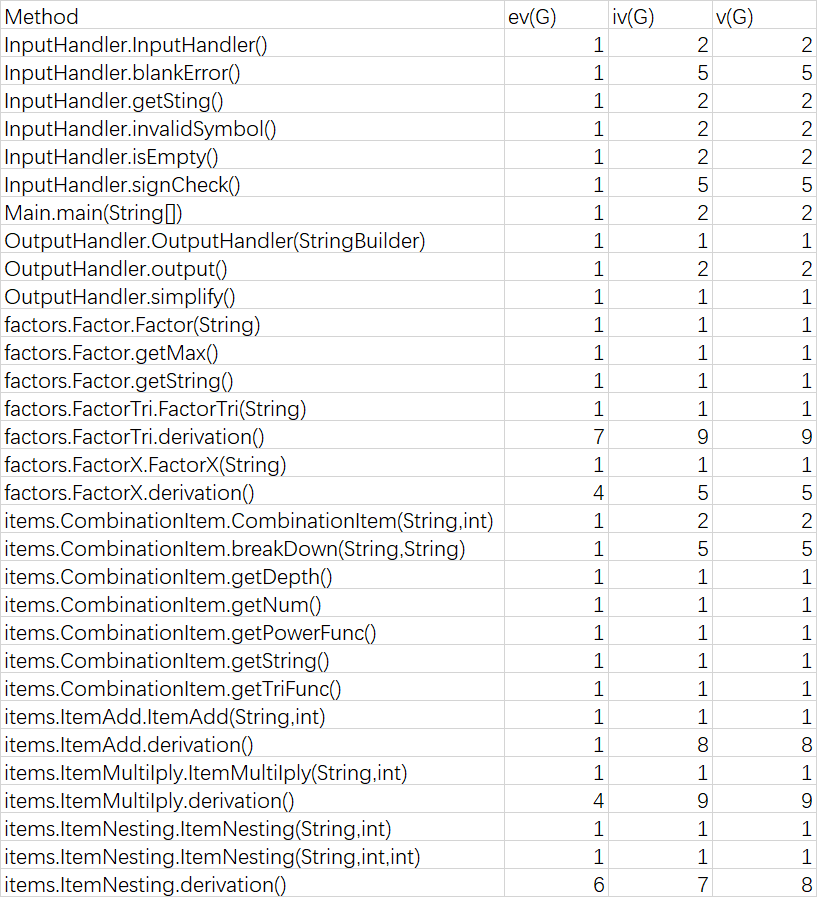
　　OCavg为平均循环复杂度;WMC为总循环复杂度

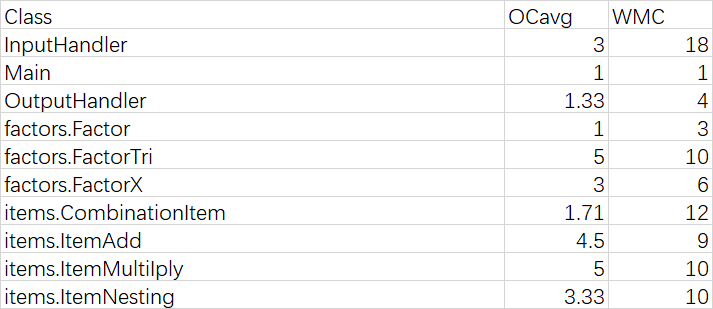
4. 分析

本次作业一共使用10个类，没有使用接口，使用了一层继承。

Main类：

　　1）程序入口

　　2）主要业务逻辑层

InputHandler类：

　　1）处理输入String

　　2）部分WF

factors包：

Factor类（父类）：

　　1）抽象函数derivation public abstract String derivation();

　　2）FactorTri类（三角函数因子类）：

　　　　2.1）将嵌套的因子用 content 保存：

　　　　　　 content = string.replaceAll("^sin\\(", "").replaceAll("\\)(\\^[+\\-]?\\d+)?$", "");

　　　　2.2）区分sin、cos private Pattern patternSin = Pattern.compile("^sin\\(");

　　　　　　　　　　　　  private Pattern patternCos = Pattern.compile("^cos\\(");

　　　　2.3）判断WF（指数>10000）

　　　　2.4）求导

　　3）FactorX类（幂函数因子类）：

　　　　3.1）求导

items包：

CombinationItem类（父类）：

　　1）定义最大递归深度（将非法数据判为WF）（每调用一次depth++）：

 if (depth > 95) {
     System.out.println("WRONG FORMAT!");
     System.exit(0);
 }

　　2）定义抽象函数derivation public abstract StringBuilder derivation();

　　3）定义函数beakdown，将str以sign分割为List ArrayList<String> breakDown(String str, String sign) ，并判断WF

　　4）ItemAdd类（加法组合项类）：

　　　　4.1） ArrayList<String> addList = breakDown(string, "+-");

　　　　4.2）对addList每一项判断

　　　　　　4.2.1）若string为表达式因子之外的因子，直接求导，以stringBuilder返回值

　　　　　　4.2.2）其他情况调用itemMultiIply类，进入下一轮递归调用

 ItemMultiIply itemMultiIply = new ItemMultiIply(addList.get(i), depth + 1);
 stringBuilder.append(itemMultiIply.derivation());

　　5）ItemMultilply类（乘法组合项类）：

　　　　5.1） ArrayList<String> multList = super.breakDown(string, "*");

　　　　5.2）链式求导，调用itemNesting类

　　6）itemNesting类（嵌套组合项类）：

　　　　6.1）判断是否有嵌套，同时判断WF

　　　　6.2）若有（）类嵌套，调用itemAdd类

　　　　6.3）若有sin()、cos()类嵌套

　　　　　　6.3.1）如果内含为表达式因子之外的因子则直接返回stringBuilder

　　　　　　6.3.2）否则调用itemAdd类（用多flag参数的构造函数并设flag=1）和FactorTri类

　　　　6.4）其他情况

　　　　　　　6.4.1）flag = 0则调用itemAdd类

　　　　　　　6.4.2）flag = 1则WF

OutputHandler类：

　　1）防止输出空字符串

　　2）输出String

（2）程序BUG分析

1.  强测中未被查出BUG，但为了保证正确性，没有做优化，性能分为0。

2. 互测中被查出1个BUG，如下：

输入	-(+(+1*cos(x)))*cos((x-cos(x)))
我的输出	-(+(((+(((+0+(-1*sin(x)*1)*1))))))*cos((x-cos(x)))+(-1*sin((x-cos(x)))*((1--1*sin(x))))*(+(+1cos(x))))
错误原因	我在处理连乘项的时候，用 replaceFirst("\\*", ""); 取代第一个乘号，但第一项前面没有*，所以替换了一二项间的*，导致出错
解决方案	用 replaceALL("^\\*", ""); 代替了上述代码，解决问题

　　这个BUG属于考虑不全面造成的错误，测试时也未覆盖到（测试样例太少，复杂测试样例更少）。　

（3）程序测试分析

　　测试方法：我用之前构造的测试样例先大致测试一遍，在观察一些易考察的部分（如：有无使用BigInteger包），进行针对性测试。

　　反思：全程手动，无自动化工具，所以效率不高，希望以后能学习使用自动化测试技术。

　　debug的部分情况如下：

输入	输出	原因
13412312235423432	WRONG FORMAT！	没用BigInteger
---2 * x	2	---识别为+
- x^+4*sin(x)^7+12*x^0001+ + +12*x-123- - x+12	WRONG FORMAT！	无法识别+ + +12
- x^+4*sin(x)^7+12*x^0001+ + +12*x-123- - x+12	-((7*sin(x)^6*cos(x)*(+1))*1+0)*(x^4)+sin(x)^7*1*(4*x^3)+12+12-0+1+0	计算错误
((sin (x ^ +1) ^ +10000))	WRONG FORMAT！	+10000认为>10000
((sin (x ^ +1) ^ +10000))	WRONG FORMAT！	中间tab无法识别
((sin (x ^ +1) ^ +10000))	java报错	创建了0长度的BigInteger

---

Applying Creational Pattern

第三次作业中用到了继承，但是没有对象构建的模式，仍旧是面向过程式的想用某个项时，特殊调用某个项。借鉴了各路大神的思路，有了初步的想法。通过一个工厂函数，将当前字符串输入，返回一个对应类的对象。代码如下：

 public static Factor factorFactory(String str) {
         if (str.contains("sin")) {
             return new FactorSin(str);
         } else if (str.contains("cos")) {
             return new FactorCos(str);
         } else {
             return new FactorX(str);
         }
 }

---

总结

1）面向对象的思维在三次作业中逐渐建立起来，但是代码实际上还是面向过程，有待改进。

2）对于java一些包的使用不熟练，只会用几个基本的包（BigInteger、ArrayList、StringBuilder等）。

3）优化太少，且多为面向数据的优化，很少建立优化规则。

4）手造测试数据太随便，应该进行分模块的覆盖性测试。

5）代码耦合度太高，需要解耦

6）好的构造思路远比“打补丁”高效

希望多思考，多实践，多看大佬分享的思路，OO加油啊~