CF922B Magic Forest

CF922B Magic Forest

题意翻译

题目大意

给定一个正整数nn ，求满足如下条件的三元组(a,b,c)(a,b,c) 的个数：

• 1 \le a \le b \le c \le n1≤a≤b≤c≤n
• a \space xor \space b \space xor \space c=0a xor b xor c=0
• 存在一个边长分别为a,b,ca,b,c 的三角形。

输入格式

一行一个正整数n(1 \le n \le 2500)n(1≤n≤2500)

输出格式

输出满足题意的三元组个数。

感谢U3144 浮尘ii 提供的翻译

题目描述

Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order nn is such a non-degenerate triangle, that lengths of its sides are integers not exceeding nn , and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order nnto get out of the forest.

Formally, for a given integer nn you have to find the number of such triples (a,b,c)(a,b,c) , that:

• 1<=a<=b<=c<=n1<=a<=b<=c<=n ;
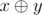• , where  denotes the bitwise xor of integers xx and yy .
• (a,b,c)(a,b,c) form a non-degenerate (with strictly positive area) triangle.

输入输出格式

输入格式：

The only line contains a single integer nn (1<=n<=2500)(1<=n<=2500) .

输出格式：

Print the number of xorangles of order nn .

输入输出样例

输入样例#1： 复制

6

输出样例#1： 复制

1

输入样例#2： 复制

10

输出样例#2： 复制

2

说明

The only xorangle in the first sample is (3,5,6)(3,5,6) .

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,ans;
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++)
        for(int j=i+;j<=n;j++){
            int k=i^j;
            if(k>n)    continue;
            if(i+j>k&&abs(i-j)<k&&i+k>j&&abs(i-k)<j&&j+k>i&&abs(j-k)<i)    ans++;
        }
    cout<<ans/;
}