福建省第八届 Triangles

Problem Description

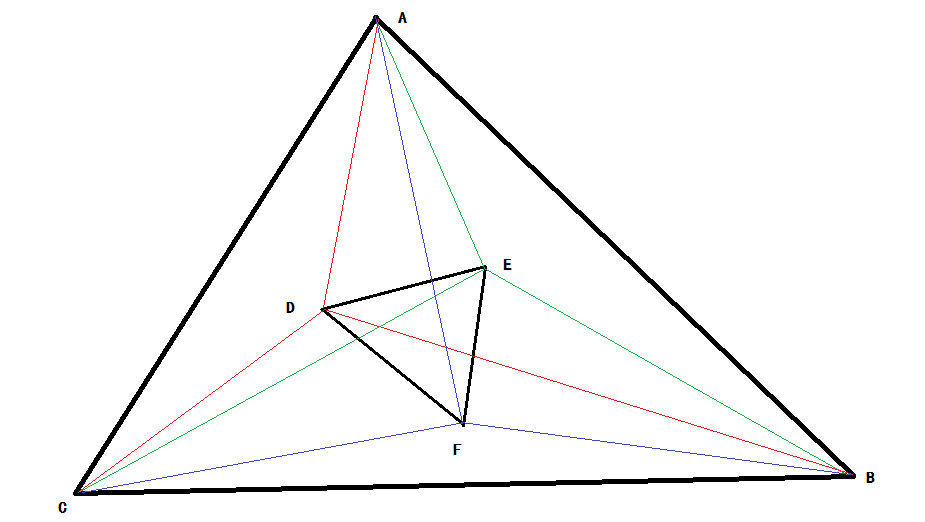
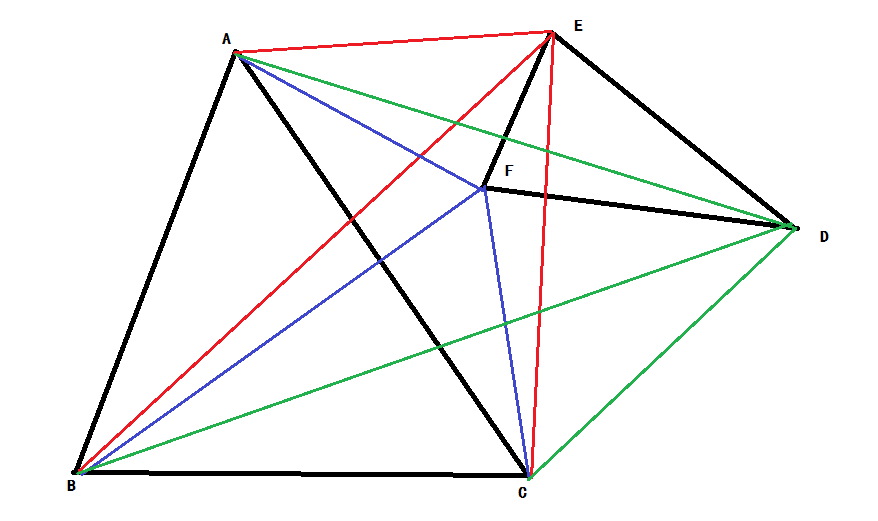
This is a simple problem. Given two triangles A and B, you should determine they are intersect, contain or disjoint. (Public edge or point are treated as intersect.)

Input

First line contains an integer T (1 ≤ T ≤ 10), represents there are T test cases.

For each test case: X1 Y1 X2 Y2 X3 Y3 X4 Y4 X5 Y5 X6 Y6. All the coordinate are integer. (X1,Y1) , (X2,Y2), (X3,Y3) forms triangles A ; (X4,Y4) , (X5,Y5), (X6,Y6) forms triangles B.

-10000<=All the coordinate <=10000

Output

For each test case, output “intersect”, “contain” or “disjoint”.

Sample Input

2 0 0 0 1 1 0 10 10 9 9 9 10 0 0 1 1 1 0 0 0 1 1 0 1

Sample Output

disjoint

intersect

判断两个三角形是 相交，包含，还是相离的关系

包含关系：

如图：若ΔDEF被包含；则可通过点来判断

D点被包含SΔACD+SΔCDB+SΔADB=SΔABC 同理判断E、F点，若三点全满足则包含

相离关系：

如图：若D点在外：则有SΔDAC+SΔDBC+SΔAB>SΔABC

若三点都满足上式，则相离，剩下的就只有相交关系了。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <iomanip>
#include <cmath>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#define lowbit(x) (x&(-x))
#define max(x,y) (x>y?x:y)
#define min(x,y) (x<y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.141592653589793238462
#define INF 0x3f3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int t,ans;
struct point
{
    double x;
    double y;
};
struct trangle
{
    point p[];
}angle[];
double area(point a,point b,point c)
{
    return fabs((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y));//三角形面积
}
bool check(trangle a,trangle b)
{
    double area_trangle=area(a.p[],a.p[],a.p[]);//判断是否包含和不相交
    int pos=;
    for(int i=;i<;i++)
    {
        if((area(b.p[i],a.p[],a.p[])+area(b.p[i],a.p[],a.p[])+area(b.p[i],a.p[],a.p[]))>area_trangle) continue;
        else ans++,pos++;
    }
    return pos==;
}
void solve()
{
    ans=;
    if(check(angle[],angle[]) || check(angle[],angle[]))
    {
        puts("contain");
        return ;
    }
    else if(!ans)
    {
        puts("disjoint");
        return ;
    }
    else
    {
        puts("intersect");
        return ;
    }
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        for(int i=;i<;i++)
        {
            for(int j=;j<;j++)
            {
                scanf("%lf%lf",&angle[i].p[j].x,&angle[i].p[j].y);
            }
        }
        solve();
    }
    return ;
}