BZOJ 4817: [Sdoi2017]树点涂色 LCT+Access的性质+DFS序+线段树

Description

Bob有一棵n个点的有根树，其中1号点是根节点。Bob在每个点上涂了颜色，并且每个点上的颜色不同。定义一条路

径的权值是：这条路径上的点（包括起点和终点）共有多少种不同的颜色。Bob可能会进行这几种操作：

1 x:

把点x到根节点的路径上所有的点染上一种没有用过的新颜色。

2 x y:

求x到y的路径的权值。

3 x

在以x为根的子树中选择一个点，使得这个点到根节点的路径权值最大，求最大权值。

Bob一共会进行m次操作 

Input

第一行两个数n,m。

接下来n-1行，每行两个数a,b，表示a与b之间有一条边。

接下来m行，表示操作，格式见题目描述

1<=n,m<=100000

Output

每当出现2,3操作，输出一行。

如果是2操作，输出一个数表示路径的权值

如果是3操作，输出一个数表示权值的最大值

题解：

和事情的相似度那道题挺像的.
都是利用 $LCT$ 中同一颗 $splay$ 中颜色相等这个性质.
这道题用线段树维护一下 DFS 序，查询的时候在 DFS 序中查询即可.
维护每个点到根节点的色块个数.
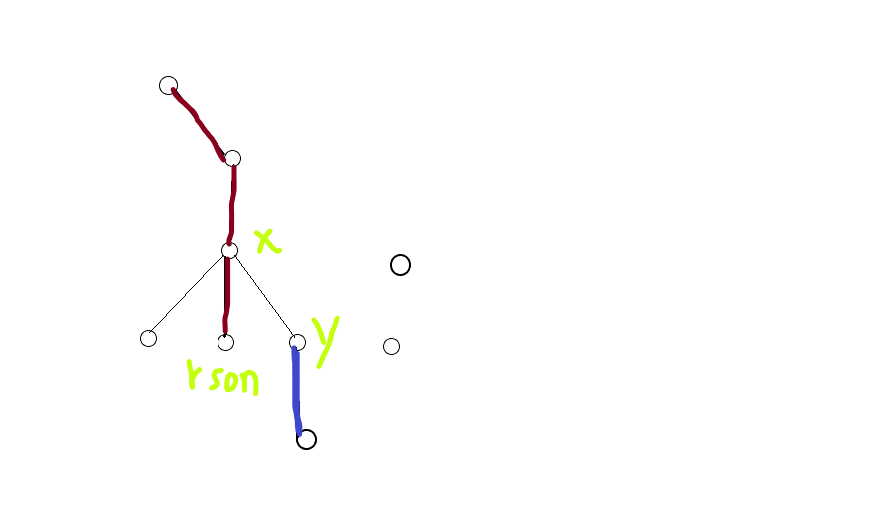
考虑染色时会产生的影响：

假设现在要把某个点到根节点路径都染成蓝色.
当前 $Access$ 时处理的点为  $x$，右儿子为 $rson$，要连接的为 $y$
那么，对于 $y$ 及其子树来说，原来有红 + 蓝，现在将只有蓝，答案减一
对于 $rson$ 及其子树来说，原来只有红，现在有红 + 蓝（ $rson$ 没被染成蓝色）
对于子树权值修改，直接上线段树即可.

 

#include<bits/stdc++.h>
#define maxn 200003
#define inf -1000000
using namespace std;
void setIO(string s)
{
	string in=s+".in",out=s+".out";
	freopen(in.c_str(),"r",stdin);
	freopen(out.c_str(),"w",stdout);
}
int tim,edges,n,Q,_curcol;
int dfn[maxn],ln[maxn],fa[maxn],hd[maxn],to[maxn<<1],nex[maxn<<1];
int st[maxn],ed[maxn],top[maxn],hson[maxn],siz[maxn],dep[maxn];
void addedge(int u,int v)
{
	nex[++edges]=hd[u],hd[u]=edges,to[edges]=v;
}
namespace tr
{
	int maxv[maxn<<2],lazy[maxn<<2];
	void mark(int x,int k)
	{
		lazy[x]+=k, maxv[x]+=k;
	}
	void pushdown(int l,int r,int x)
	{
		if(!lazy[x]) return;
		int mid=(l+r)>>1;
		if(mid>=l) mark(x<<1,lazy[x]);
		if(r>mid) mark((x<<1)|1,lazy[x]);
		lazy[x]=0;
	}
	void update(int l,int r,int x,int L,int R,int k)
	{
		if(l>=L&&r<=R)
		{
			mark(x,k);
			return;
		}
		pushdown(l,r,x);
		int mid=(l+r)>>1;
		if(L<=mid) update(l,mid,x<<1,L,R,k);
		if(R>mid) update(mid+1,r,(x<<1)|1,L,R,k);
		maxv[x]=max(maxv[x<<1],maxv[(x<<1)|1]);
	}
	int query(int l,int r,int x,int L,int R)
	{
		if(l>=L&&r<=R) return maxv[x];
		pushdown(l,r,x);
		int mid=(l+r)>>1, tmp=inf;
		if(L<=mid) tmp=max(tmp,query(l,mid,x<<1,L,R));
		if(R>mid) tmp=max(tmp,query(mid+1,r,(x<<1)|1,L,R));
		return tmp;
	}
	int po(int l,int r,int x,int k)
	{
		if(l==r) return maxv[x];
		int mid=(l+r)>>1;
		pushdown(l,r,x);
		if(k<=mid) return po(l,mid,x<<1,k);
		else return po(mid+1,r,(x<<1)|1,k);
	}
};
namespace tree
{
	#define lson ch[x][0]
	#define rson ch[x][1]
	#define get(x) (ch[f[x]][1]==x)
	#define isrt(x) (!(ch[f[x]][0]==x||ch[f[x]][1]==x))
	int ch[maxn][2],f[maxn],col[maxn],sta[maxn];
	void pushdown(int x)
	{
		if(!x) return;
		if(col[x])
		{
			if(lson) col[lson]=col[x];
			if(rson) col[rson]=col[x];
		}
	}
	int findrt(int x)
	{
		while(lson)x=lson;
		return x;
	}
	void rotate(int x)
	{
		int old=f[x],fold=f[old],which=get(x);
		if(!isrt(old)) ch[fold][ch[fold][1]==old]=x;
		ch[old][which]=ch[x][which^1], f[ch[old][which]]=old;
		ch[x][which^1]=old,f[old]=x,f[x]=fold;
	}
	void splay(int x)
	{
		int u=x,v=0,fa;
		sta[++v]=u;
		while(!isrt(u)) sta[++v]=f[u],u=f[u];
		while(v) pushdown(sta[v--]);
		for(u=f[u];(fa=f[x])!=u;rotate(x))
			if(f[fa]!=u)
				rotate(get(fa)==get(x)?fa:x);
	}
	void Access(int x,int co)
	{
		int t=0,son;
		while(x)
		{
			splay(x);
			if(t) son=findrt(t), tr::update(1,n,1,st[son],ed[son],-1);
			if(rson) son=findrt(rson),tr::update(1,n,1,st[son],ed[son],1);
			col[x]=co,rson=t,t=x,x=f[x];
		}
	}
};
void dfs1(int u,int ff)
{
	fa[u]=ff;
	siz[u]=1;
	dep[u]=dep[ff]+1;
	ln[++tim]=u;
	dfn[u]=st[u]=tim;
	tr::update(1,n,1,dfn[u],dfn[u],dep[u]);
	tree::f[u]=ff;
	for(int i=hd[u];i;i=nex[i])
	{
		int v=to[i];
		if(v==ff) continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>siz[hson[u]]) hson[u]=v;
	}
	ed[u]=tim;
}
void dfs2(int u,int tp)
{
	top[u]=tp;
	if(hson[u]) dfs2(hson[u],tp);
	for(int i=hd[u];i;i=nex[i])
	{
		int v=to[i];
		if(v==hson[u]||v==fa[u]) continue;
		dfs2(v,v);
	}
}
int LCA(int x,int y)
{
	while(top[x]^top[y]) dep[top[x]] < dep[top[y]] ? y = fa[top[y]] : x = fa[top[x]];
	return dep[x] < dep[y] ? x : y;
}
int main()
{
	// setIO("input");
	scanf("%d%d",&n,&Q);
	tr::maxv[0]=inf;
	for(int i=1,u,v;i<n;++i)
	{
		scanf("%d%d",&u,&v);
		addedge(u,v);
		addedge(v,u);
	}
	dfs1(1,0);
	dfs2(1,1);
	int opt,x,y,lca,ou=0;
	while(Q--)
	{
		scanf("%d",&opt);
		switch(opt)
		{
			case 1 :
			{
				scanf("%d",&x);
				tree::Access(x,++_curcol);
				break;
			}
			case 2 :
			{
				scanf("%d%d",&x,&y);
				lca=LCA(x,y);
				ou=0;
				ou+=tr::po(1,n,1,dfn[x]);
				ou+=tr::po(1,n,1,dfn[y]);
				ou-=tr::po(1,n,1,dfn[lca])<<1;
				ou+=1;
				printf("%d\n",ou);
				break;
			}
			case 3 :
			{
				scanf("%d",&x);
				printf("%d\n",tr::query(1,n,1,st[x],ed[x]));
				break;
			}
		}
	}
	return 0;
}