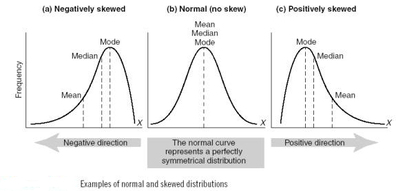
正态分布（normal distribution）与偏态分布（skewed distribution）

存在正太分布的概念，自然也少不了偏态分布。

• 正态分布（normal distribution）
• 偏态分布（skewed distribution）
  
  • 左偏态：left skewed distribution，负偏态（negatively skewed distribution），以尾部命名，左偏态或者叫负偏态的尾部，主要在左侧；
  • 右偏态：right skewed distribution，正偏态（positively skewed distribution），同样地，右偏态或者叫正偏态的尾部，则集中在右侧；
• 正态分布还是偏态分布（左偏态/右偏态）在函数图像上容易分辨，在统计数据上，也很容易分别，比如正偏态分布，mean > median，对于负偏态，mean < median,

1. 正态分布数字特征

• 均值或者期望：

  E[x]=∫∞−∞xN(μ,σ2)dx=μ

• 二阶矩：

  E[x2]=∫∞−∞x2N(μ,σ2)dx=μ2+σ2

• 方差：

  var[x]=E[x2]−(E[x])2=σ2