机器学习——SVM讲解

支持向量机（Support Vector Machine）

SVM是一类按监督学习方式对数据进行二元分类的广义线性分类器，决策边界是对学习样本求解的最大边距超平面。只需要知道，SVM是一个有监督的分类器就可以。

介绍SVM首先要从核函数的介绍开始，SVM是一个处理线性可分离数据的线性分类器。对于下方右边的数据时，SVM不能很好的应对。

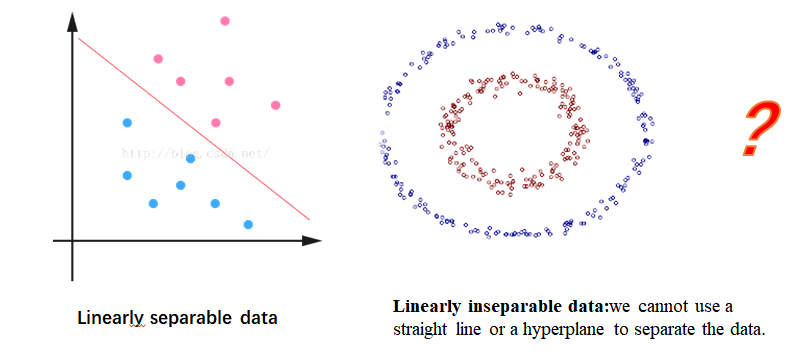
情况一：在对于线性不可分数据时，应该如何应对？将低维数据转换为高维数据可以将线性不可分数据转化为线性可分的数据。如下图所示：

情况二：当数据用直线不可分时：

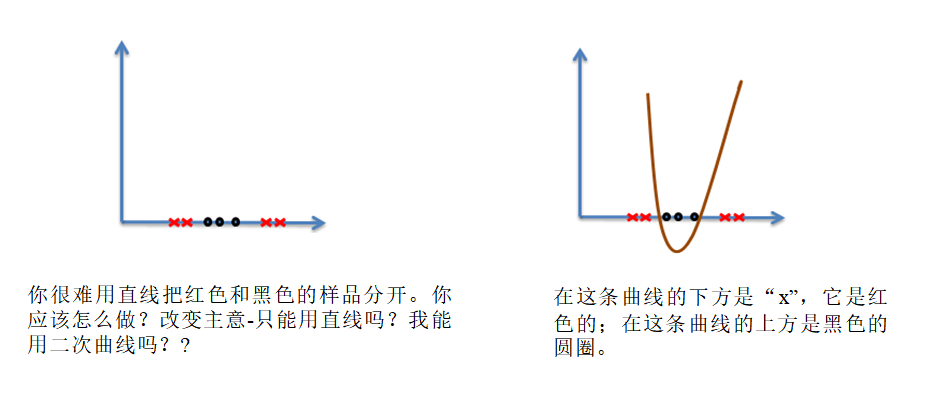
原来的线性方程为：F(x) = wx+b，当遇到上述情况时，无法有效的进行分类处理。我们可以用二次函数，进行区分。

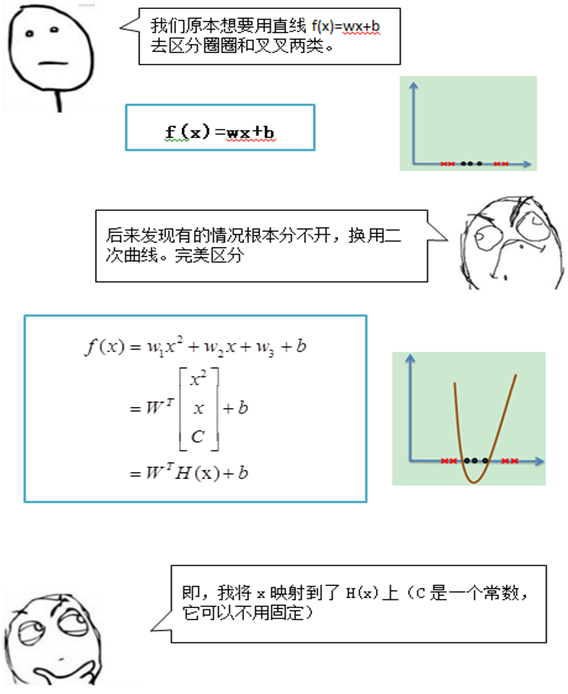
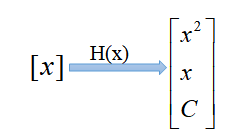
其中，我们将原始的一维映射为三维：

首先我们通过对偶问题的转折，将原来的SVM目标函数转化为以下形式：

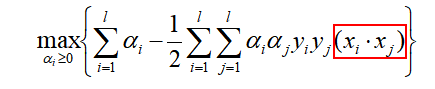
在这种情况下，x应该被替换为H（x）：

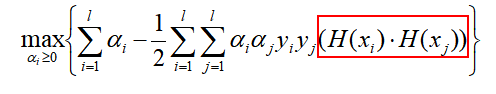
那么，什么是核函数？在计算中，可以使x1和x2不通过H(*)映射到高维空间计算内积，而是直接在低维空间计算。我们使用K(*)来表示核函数，核函数的作用是：

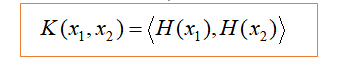避免一个从低维到高维的映射过程。

举个例子：

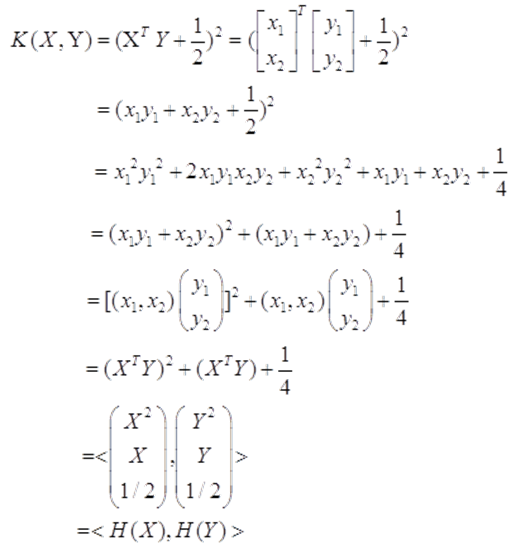
在本例中，低维核函数计算的结果与原始问题完全等效，因此，我们避免了在高维空间中进行直接计算。那么问题来了，核函数是固定的吗？显然不是，核函数有很多种，根据问题和数据之间的差异选择适当的核函数。本文列举了几种常见的核函数如下所示：

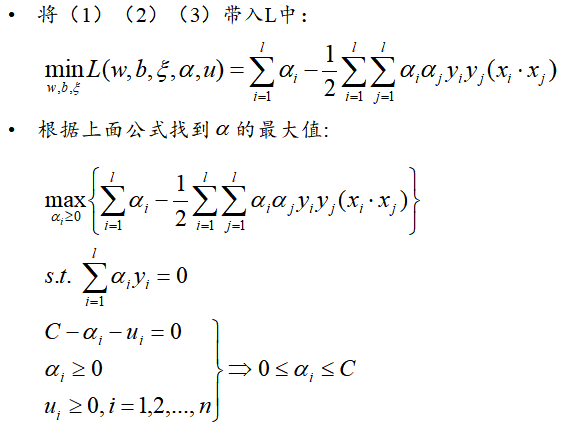
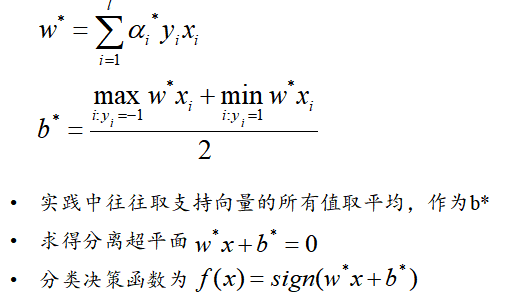
总结：

SVM是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。或者简单的可以理解为就是在高维空间中寻找一个合理的超平面将数据点分隔开来，其中涉及到非线性数据到高维的映射以达到数据线性可分的目的。