「 JSOI2004」「LuoguP1337」平衡点 / 吊打XXX（模拟退火

题目描述

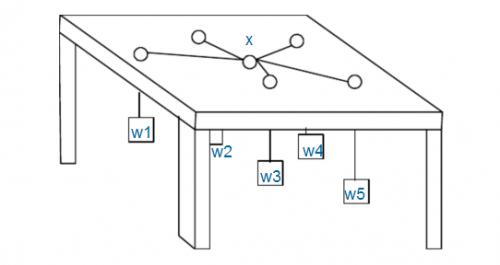
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

输出格式：

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

输入输出样例

输入样例#1：复制

输出样例#1：复制

0.577 1.000

说明

[JSOI]

题解

这道题一开始看到觉得要向量什么的......计算几何?!qwq

对同学讲的在$\sum_{i=1}^{n}l_i*w_i$取最小值时最优也不是很能理解......

然后题解中有一种说法↓

觉得还是能强行理解的。（大概模拟退火都需要神仙思路吧qwq

然后就套模拟退火的板子就行了。

调(试)参(探)过程中感受了一下srand(19*****7)的魅力，和clock()/CLOCKS_PER_SEC的神仙用途。

//就是听说clock()很慢qwq，不知道用来优化爆搜效果好不好

然后就是代码了qwq↓

 /*

 qwerta

 P1337 [JSOI2004]平衡点 / 吊打XXX Accepted

 100

 代码 C++，1.05KB

 提交时间 2018-11-01 18:28:16

 耗时/内存 7005ms, 816KB

 */

 #include<iostream>

 #include<cstdlib>

 #include<cstdio>

 #include<ctime>

 #include<cmath>

 using namespace std;

 struct emm{

     int x,y,w;

 }a[];

 int n;

 double check(double x,double y)//返回(x,y)的那个sum值

 {

     double now=;

     for(int i=;i<=n;++i)

     {

         double mx=a[i].x-x,my=a[i].y-y;

         now+=sqrt(mx*mx+my*my)*a[i].w;

     }

     return now;

 }

 double ansx,ansy,ans;

 double t,tmin=1e-;

 double deltt=0.993;

 void SA()//板子

 {

     double x=ansx,y=ansy;

     t=;//2333不给过，被改成6000就过掉了qwq

     while(t>tmin)

     {

         double tox=x+((rand()<<)-RAND_MAX)*t;

         double toy=y+((rand()<<)-RAND_MAX)*t;

         double now=check(tox,toy);

         double delt=now-ans;

         if(delt<)

         {

             ans=now,ansx=tox,ansy=toy;

             x=tox,y=toy;

         }

         else if(exp(-delt/t)*RAND_MAX>rand()){x=tox,y=toy;}

         t*=deltt;

     }

     return;

 }

 int main()

 {

     //freopen("a.in","r",stdin);

     srand();srand(rand()),srand(rand());

     scanf("%d",&n);

     int totx,toty;

     for(int i=;i<=n;++i)

     {

         scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].w);

         totx+=a[i].x,toty=a[i].y;

     }

     ans=1e14+,ansx=totx/n,ansy=toty/n;//从中间开始跑

     while((double)clock()/CLOCKS_PER_SEC<0.75)//如果用掉的时间还不超过0.75秒

     SA();

     printf("%.3f %.3f",ansx,ansy);

     return ;

 }

吸毒真香