【费用流】 ICPC 2016 China Final J. Mr.Panda and TubeMaster

表示“必须选”的模型

题目大意

---

题目分析

一个格子有四种方式看上去很难处理。将横竖两个方向分开考虑，会发现：因为收益只与相邻格子是否连通有关，所以可以将一个格子拆成表示横竖两个方向的，互相独立的点。

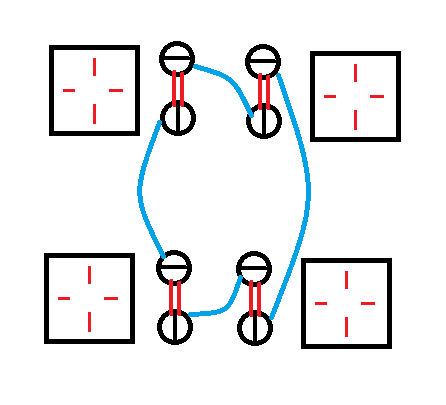
上图的格子里四个方向红边表示的就是一个格子的可能方向；拆点后所连蓝边的容量为1，费用即为连通两个格子的收益。

但是这样建图不能够表示某些格子必须要选。

考虑一个格子如果被选择了会发生什么：因为每个格子都处在环上，那么被选择的网格一定可以通过其他节点走到汇点。这意味着一个格子拆成的两个节点之间的边就可以先不建，而若最大流不等于网格总数，即有节点不可能被合法选中。

建图的时候一定要先理解清楚，因为有很多种错误方式，下图就是其中一个。

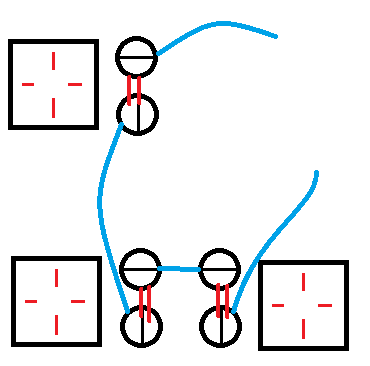
 #include<queue>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<algorithm>
 const int maxn = ;
 const int maxm = ;
 const int INF = 2e9;

 struct Edge
 {
     int u,v,f,c,cst;
     Edge(int a=, int b=, int c=, int d=, int e=):u(a),v(b),f(c),c(d),cst(e) {}
 }edges[maxm];
 int sne,n,m,S,T;
 bool ess[][],inq[maxn];
 int tagl[][],tagr[][],valc[][],valr[][];　　//tagl为入点，tagr为出点
 int edgeTot,head[maxn],nxt[maxm],flw[maxn],cst[maxn],bck[maxn];

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v, int c, int cst)
 {
     edges[edgeTot] = Edge(u, v, , c,  cst), nxt[edgeTot] = head[u], head[u] = edgeTot++;
     edges[edgeTot] = Edge(v, u, , , -cst), nxt[edgeTot] = head[v], head[v] = edgeTot++;
 }
 void maxFlow()
 {
     int mxFlw = , cost = ;
     for (;;)
     {
         std::queue<int> q;
         memset(flw, , sizeof flw);
         memset(bck, , sizeof bck);
         memset(cst, 0x3f3f3f3f, sizeof cst);
         q.push(S), flw[S] = INF, cst[S] = ;
         for (int tmp; q.size(); )
         {
             tmp = q.front(), q.pop(), inq[tmp] = ;
             for (int i=head[tmp]; i!=-; i=nxt[i])
             {
                 int v = edges[i].v;
                 if (cst[tmp]+edges[i].cst < cst[v]&&edges[i].f < edges[i].c){
                     bck[v] = i, cst[v] = cst[tmp]+edges[i].cst;
                     flw[v] = std::min(flw[tmp], edges[i].c-edges[i].f);
                     if (!inq[v]) inq[v] = , q.push(v);
                 }
             }
         }
         if (!flw[T]) break;
         for (int i=T; i!=S; i=edges[bck[i]].u)
             edges[bck[i]].f += flw[T], edges[bck[i]^].f -= flw[T];
         mxFlw += flw[T], cost += cst[T]*flw[T];
     }
     if (mxFlw!=n*m) puts("Impossible");
     else printf("%d\n",-cost);
 }
 int main()
 {
     sne = read();
     for (int cse=; cse<=sne; cse++)
     {
         printf("Case #%d: ",cse);
         memset(ess, , sizeof ess);
         memset(head, -, sizeof head);
         edgeTot = , n = read(), m = read();
         for (int i=; i<=n; i++)
             for (int j=; j<m; j++)
                 valc[i][j] = read();
         for (int i=; i<n; i++)
             for (int j=; j<=m; j++)
                 valr[i][j] = read();
         for (int i=, cnt=; i<=n; i++)
             for (int j=; j<=m; j++)
                 tagl[i][j] = ++cnt, tagr[i][j] = ++cnt;
         S = , T = tagr[n][m]+;
         for (int i=; i<=n; i++)
             for (int j=; j<=m; j++)
                 if ((i+j)&){　　　　//为避免重复建边的处理技巧
                     if (j+ <= m) addedge(tagl[i][j], tagr[i][j+], , -valc[i][j]);
                     if (j- >= ) addedge(tagl[i][j], tagr[i][j-], , -valc[i][j-]);
                 }else{
                     if (i+ <= n) addedge(tagl[i][j], tagr[i+][j], , -valr[i][j]);
                     if (i+ >= ) addedge(tagl[i][j], tagr[i-][j], , -valr[i-][j]);
                 }
         for (int i=read(); i; i--) ess[read()][read()] = ;
         for (int i=; i<=n; i++)
             for (int j=; j<=m; j++)
             {
                 addedge(S, tagl[i][j], , );
                 addedge(tagr[i][j], T, , );
                 if (!ess[i][j]) addedge(tagl[i][j], tagr[i][j], , );
             }
         maxFlow();
     }
     return ;
 } 

END