查找系列合集-二叉查找树BST
一、 二叉树
1. 什么是二叉树？
在计算机科学中，二叉树是每个结点最多有两个子树的树结构。
通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。
二叉树常被用于实现二叉查找树和二叉堆。
2. 二叉树是一个递归的定义
（1）根结点为空则定义该二叉树为空
（2）一个根结点，可以导出一棵完整的二叉树，而它的左孩子或者右孩子，同样可以是代表一棵完整二叉树的根结点，不论它是否为空。即左子树和右子树同样为二叉树。
3. 二叉堆
（1）二叉堆一般由数组实现，分为大根堆和小根堆，可以实现O（1）的时间查找最大值（最小值）。
（2）插入一个元素O（logN）,先插到末尾，然后通过swim操作上浮调整，保持堆结构
（3）删除一个元素O（logN）,先把头尾元素交换，删去尾，对头进行sink操作下沉调整，保持堆结构。
（4）详情可见另外一篇博客排序系列及其拓展优化 中的基于堆的优先队列实现
二、 基于数组的二叉查找树
1. 保证数组有序
2. 通过【二分】的方法实现对数时间内查找
3. 由于是数组，要保持元素个数变化后数组依然有序，则插入和删除必然导致有一段元素需要整体移动，因此代价是O（N）
4. 基于数组的二叉查找树和堆的区别？为什么堆能保持对数级别的插入和删除？
（1）二叉查找树和堆虽然都基于数组，但是前者的数组有序，而后者只是保持堆结构（堆结构只是顶头元素是最值但是不是整体有序）
（2）二叉查找树可以查找任意关键字的元素，而堆是为了保持顶头元素的最值特性并不具备优秀的查找功能。
5. 代码实现
package search; import java.util.Random;
/*
* 基于有序数组的二叉搜索树
* */
public class BinarySearchST<Key extends Comparable<Key> , Value> {
private Key[] keys; //键
private Value[] vals; //值
private int N;// 当前使用容量 public BinarySearchST(int capacity) {
keys = (Key[]) new Comparable[capacity];
vals = (Value[]) new Object[capacity];
} public int size() {
return N;
}
//根据键来查找对应值
public Value get(Key key) {
//找出该键在数组中的下标
int pos = rank(key);
//如果找到的下标在范围内并且确实是这个键，说明找到了
if(pos < N && keys[pos].compareTo(key) == 0) {
return vals[pos];
}
else return null;//否则没有找到，返回空
}
//二分法查找键的位置
public int rank(Key key) {
int lo = 0, hi = N - 1;
//二分查找
while(lo <= hi) {
int mid = lo + (hi - lo) / 2;
if(keys[mid].compareTo(key) > 0) {
hi = mid - 1;
}
else if(keys[mid].compareTo(key) < 0 ) {
lo = mid + 1;
}
else {
return mid;
}
}
//如果找不到 之前一步lo必定等于hi， 看这个数字是大于还是小于，不论怎样，lo的位置都代表如果这个数存在
//它应该处于的位置
return lo;
} public void put(Key key, Value val) {
int pos = rank(key);//先看这个键有木有
//如果有只需要修改一下值就行了
if(pos < N && keys[pos].compareTo(key) == 0) {
vals[pos] = val;
}
//如果没有就新建一个键值对 插入
//插入的位置正好是pos 那么pos之后的数都要后移一位
//如果容量已满需要扩容
for(int i=N-1; i>=pos; i--) {
keys[i + 1] = keys[i];
vals[i + 1] = vals[i];
}
//空出来的位置插入新键值对
keys[pos] = key;
vals[pos] = val;
N++;
} public void delete(Key key) {
int pos = rank(key);//先看这个键有木有
//如果有就删除 并且后移一位
if(pos < N && keys[pos].compareTo(key) == 0) {
for(int i=pos; i<N-1; i++) {
keys[i] = keys[i+1];
vals[i] = vals[i+1];
}
N--;
}
//如果没有就返回
return;
} public void show() {
for(int i=0; i<N; i++) {
System.out.println(keys[i].toString() + " : " + vals[i].toString());
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
BinarySearchST<Integer, Integer> bs = new BinarySearchST<Integer , Integer>(20);
Random r = new Random();
for(int i=0; i<10; i++) {
Integer t1 = new Integer(r.nextInt(1000));
Integer t2 = new Integer(r.nextInt(1000));
bs.put(t1, t2);
}
bs.show();
System.out.println("size = " + bs.size());
System.out.println("*********************");
bs.put(999, 999);
bs.put(555, 555);
bs.show();
System.out.println("size = " + bs.size());
System.out.println("*********************");
bs.delete(555);
bs.delete(1024);
bs.show();
System.out.println("size = " + bs.size());
} }
三、 基于链表的二叉查找树BST
1. 结点结构
private class Node{
private Key key;//键
private Value val;//值
private Node left , right;//左孩子和右孩子
private int N ; //该子树的总结点个数
public Node() {}
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
2. BST类结构
public class BST<Key extends Comparable<Key> , Value> {
private Node root;
private class Node{...}//结点内部类声明
//一系列方法
}
3. 核心方法：增删改查
（1）查找
a. 基于二分
b. 利用树天生的递归特性，递归查找
//根据键找值
public Value get(Key key) {
return get(root , key);
}
private Value get(Node x, Key key) {
if(x == null) return null;
int cmp = x.key.compareTo(key);
if(cmp == 0) return x.val;
else if(cmp > 0) return get(x.left , key);
else return get(x.right , key);
}
（2）插入
a. 插入从某种意义上包括了修改，因为改某一个键所对应的值只需要插入同键不同值即可。
b. 插入总是被插入到了某一个结点的空的左右子结点中
public void put(Key key, Value val) {
root = put(root , key, val);
}
private Node put(Node x , Key key, Value val) {
//如果没有这个键就新增一个
if(x == null) {
return x = new Node(key , val, 1);
}
//沿途二分找键，遇到的根节点键大，则在其左子树递归查找，键小，在右子树递归查找，
//直到找到相等或者发现根节点为空为止
int cmp = x.key.compareTo(key);
if(cmp > 0) {
x.left = put(x.left , key, val);
}
else if(cmp < 0) {
x.right = put(x.right , key , val);
}
else {
x.val = val;
}
//沿途回溯更新结点的size 自底向上
x.N = size(x.left) + size(x.right) + 1;
return x;
}
（3）删除
删除是BST的最复杂的操作，先考虑一下几种情况 ,假设被删除的结点记为z：
（a）z左右孩子均为空。这种情况十分简单，直接删除这个结点即可，正棵BST仍然有序
（b）z有一个孩子不空。不妨假设右孩子不空，那么只需要把z.right 作为z的父节点x的新的孩子结点即可。
比如结点x.right = z, 则只需要把x.right = z.right 即可，（x.left = z同理）BST有序性不变
（c）z的左右孩子均不空。
- 假设z的父节点为x，且x.left = z （x.right = z同理可得）
- 首先把 z 暂存，存为结点 t
- 找z的右子树的最小结点（该操作为deleteMin(Node x)），不妨设为y，则y.left必为空，并且满足t.left < y < t.right。也就是说，如果把y结点放到要删除的z结点的位置，树还是有序的
- 把z结点指针指向y (z和y是同一结点), 把按照（b）情况删除结点z并返回z结点，注意经过b操作后，此时z的父节点与z的右孩子结点已经连接
- 把z的左右孩子设置为t的左右孩子
- x.left = z即可。
- 若看不明白只需要记住加黑字体是该算法的主要思想，详情见代码。
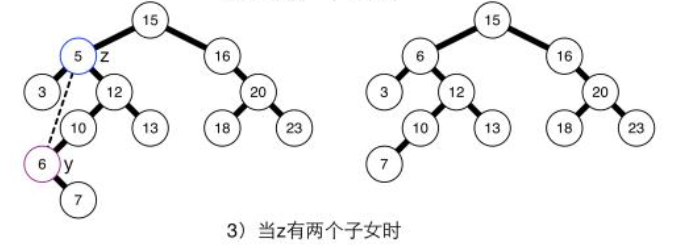
【代码实现】
//删除一棵树的最小结点
public void deleteMin() {
root = deleteMin(root);
} private Node deleteMin(Node x) {
// TODO Auto-generated method stub
if(x.left != null) {
x.left = deleteMin(x.left);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
return x.right;
} public void delete(Key key) {
root = delete(root , key);
}
public Node delete(Node x, Key key) {
if(x == null) return null;
int cmp = x.key.compareTo(key);
if(cmp > 0) {
x.left = delete(x.left , key);
}
else if(cmp < 0) {
x.right = delete(x.right , key);
}
else {
//找到要删除的结点了
if(x.left == null) return x.right;
if(x.right == null) return x.left; Node t = x;
x = minK(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
}
4. 其他操作
- public Key ceiling(Key key) //返回大于等于key的最大值所在结点
public Keyfloor(Key key) //返回小于等于key的最大值所在结点
- public Key select(int k) //查找排名为K的键(树中恰好有K个小于他的键)
- public ...... //其他操作
四、 BST数据结构源码
package search; import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Random; public class BST<Key extends Comparable<Key> , Value> {
private Node root;
//结点内部类声明
private class Node{
private Key key;//键
private Value val;//值
private Node left , right;//左孩子和右孩子
private int N ; //该子树的总结点个数
public Node() {}
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
} }
public int size(){
return size(root);
}
private int size(Node x) {
if(x == null) return 0;
return x.N;
}
//根据键找值
public Value get(Key key) {
return get(root , key);
}
private Value get(Node x, Key key) {
if(x == null) return null;
int cmp = x.key.compareTo(key);
if(cmp == 0) return x.val;
else if(cmp > 0) return get(x.left , key);
else return get(x.right , key);
}
public void put(Key key, Value val) {
root = put(root , key, val);
}
private Node put(Node x , Key key, Value val) {
//如果没有这个键就新增一个
if(x == null) {
return x = new Node(key , val, 1);
}
//沿途二分找键，遇到的根节点键大，则在其左子树递归查找，键小，在右子树递归查找，
//直到找到相等或者发现根节点为空为止
int cmp = x.key.compareTo(key);
if(cmp > 0) {
x.left = put(x.left , key, val);
}
else if(cmp < 0) {
x.right = put(x.right , key , val);
}
else {
x.val = val;
}
//沿途回溯更新结点的size 自底向上
x.N = size(x.left) + size(x.right) + 1;
return x;
} //返回键的最小值
public Key minK() {
return minK(root).key;
}
private Node minK(Node x) {
if(x.left != null) {
return minK(x.left);
}
return x;
}
//返回键的最小值
public Key maxK() {
return maxK(root).key;
}
private Node maxK(Node x) {
if(x.right != null) {
return maxK(x.right);
}
return x;
}
//返回小于等于key的最大值
public Key floor(Key key) {
Node x = floor(root , key);
if(x != null) return x.key;
return null;
} //返回小于等于key的最大值所在结点
private Node floor(Node x , Key key) {
if(x == null) return null;
//比较当前根节点的键值是否大于key
int cmp = x.key.compareTo(key);
if(cmp == 0) return x;
//如果根结点的键值小于key，那么小于等于key的键值有可能在根节点的右子树中，如果没有则就是根节点
else if(cmp < 0) {
Node t = floor(x.right , key);
if(t == null) return x;
else {
return t;
}
}
//如果根节点的键值大于key，则小于等于key的键值必定在根节点的左子树中
else {
return floor(x.left , key);
}
} public Key ceiling(Key key) {
Node x = ceiling(root , key);
if(x != null) return x.key;
return null;
} //返回大于等于key的最小值所在结点
private Node ceiling(Node x , Key key) {
if(x == null) return null;
//比较当前根节点的键值是否大于key
int cmp = x.key.compareTo(key);
if(cmp == 0) return x;
//如果根节点的键值大于key，则大于等于key的键值有可能在根节点的左子树中，如果没有就是根节点
else if(cmp > 0) {
Node t = ceiling(x.left , key);
if(t == null) return x;
else {
return t;
}
}
//如果根结点的键值小于key，那么大于等于key的键值一定在根节点的右子树中
else {
return ceiling(x.right , key);
}
} //查找排名为K的键(树中恰好有K个小于他的键)
public Key select(int k) {
Node x = select(root , k);
if(x == null) return null;
return x.key;
}
private Node select(Node x , int k) {
if(x == null) return null;
int t = size(x.left);
if( t > k) {
return select(x.left , k);
}
else if(t == k) {
return x;
}
else {
return select(x.right , k - t - 1);
}
} //给定一个键求其排名(即求有多少个键小于它)
public int rank(Key key) {
return rank(root , key);
}
private int rank(Node x , Key key) {
if(x == null) return 0;
int cmp = x.key.compareTo(key);
if(cmp == 0) {
return size(x.left);
}
else if(cmp > 0) {
return rank(x.left , key);
}
else {
return size(x.left) + rank(x.right , key) + 1;
}
} //删除一棵树的最小结点
public void deleteMin() {
root = deleteMin(root);
} private Node deleteMin(Node x) {
// TODO Auto-generated method stub
if(x.left != null) {
x.left = deleteMin(x.left);
x.N = size(x.left) + size(x.right) + 1;
return x;
}
return x.right;
} public void delete(Key key) {
root = delete(root , key);
}
public Node delete(Node x, Key key) {
if(x == null) return null;
int cmp = x.key.compareTo(key);
if(cmp > 0) {
x.left = delete(x.left , key);
}
else if(cmp < 0) {
x.right = delete(x.right , key);
}
else {
//找到要删除的结点了
if(x.left == null) return x.right;
if(x.right == null) return x.left; Node t = x;
x = minK(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.N = size(x.left) + size(x.right) + 1;
return x;
} //返回整棵树的迭代对象
public Iterable<Key> keys(){
return keys(minK() , maxK());
} //返回范围[lo , hi]内所有key的迭代对象
public Iterable<Key> keys(Key lo, Key hi) {
// TODO Auto-generated method stub
Queue<Key> queue = new LinkedList<Key>();
keys(root , queue, lo, hi);
return queue;
}
//把[lo , hi]范围内的所有元素加入指定迭代对象中
private void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
// TODO Auto-generated method stub
if(x == null) return ;
int cmplo = x.key.compareTo(lo);
int cmphi = x.key.compareTo(hi);
//如果根节点大于lo说明根节点的左子树可能还有元素在此范围内
if(cmplo > 0) {
keys(x.left, queue, lo, hi);
}
//如果根节点小于hi说明根节点的右子树可能还有元素在此范围内
if(cmphi < 0) {
keys(x.right, queue, lo, hi);
}
//遇到一个结点在此范围内就将其加入集合
if(cmplo >= 0 && cmphi <= 0) {
queue.add(x.key);
}
}
//前序遍历 左中右遍历 顺序遍历
public void show(Node x) {
if(x != null) {
show(x.left);
System.out.println(x.key.toString() + " : " + x.val.toString());
show(x.right);
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
BST bst = new BST<Integer , Integer>();
Random r = new Random();
for(int i=0; i<10; i++) {
Integer key = new Integer(r.nextInt(1000));
Integer value = new Integer(r.nextInt(1000));
System.out.println("key = " + key + " value = " + value);
bst.put(key, value);
}
System.out.println("put 操作完毕");
// 186 244 336 481 507 514 663 729 743 759 761 891
bst.show(bst.root); System.out.println("show 操作完毕"); //bst.put(759, 19999);
//bst.put(761, 19999);
System.out.println(bst.get(9999));
System.out.println(bst.get(8888)); System.out.println(bst.floor(760));
System.out.println(bst.ceiling(760));
System.out.println(bst.maxK());
System.out.println(bst.select(0));
System.out.println(bst.rank(0));
bst.deleteMin();
bst.put(1000, 9999);
bst.show(bst.root);
bst.delete(1000);
bst.show(bst.root);
System.out.println("################");
Iterable<Integer> it = bst.keys(200,600);
for(Integer i : it) {
System.out.print(i.toString() + " ");
}
} }
查找系列合集-二叉查找树BST的更多相关文章
- android 图像处理系列合集
为了便于大家对滤镜算法的学习,以后发布的图像处理滤镜系列帖子会在这里汇总,本人第一次写合集,写得不好的地方大家请见谅,手头上虽然有一些滤镜的算法,但是大多不是android版的,教程里的代码大多是我借 ...
- 【查找结构 2】二叉查找树 [BST]
当所有的静态查找结构添加和删除一个数据的时候,整个结构都需要重建.这对于常常需要在查找过程中动态改变数据而言,是灾难性的.因此人们就必须去寻找高效的动态查找结构,我们在这讨论一个非常常用的动态查找树— ...
- 少儿编程|Scratch编程教程系列合集，总有一款适合你
如果觉得资源不错,友情转发,贵在分享!!! 少儿编程Scratch: 少儿编程Scratch第一讲:Scratch完美的初体验少儿编程Scratch第二讲:奇妙的接球小游戏少儿编程Scratch第三讲 ...
- Java 基础系列合集
Java基础知识你知道多少? Java特性 Java三大特性:封装,继承,多态 Java 抽象类与接口 Java 浅拷贝和深拷贝 Java static和final Java 内部类.静态内部类.匿名 ...
- 53. spring boot系列合集【从零开始学Spring Boot】
前40章节的spring boot系列已经打包成PDF在csdn进行发布了,如果有需要的可以进行下载. 下载地址:http://download.csdn.net/detail/linxinglian ...
- Android基础系列合集
四大组件 1.Service Android四大组件-Service Android-远程Service Service 动态更新 UI 2.Activity Android四大组件-Activity ...
- MySQL:系列合集
MySQL一:初识数据库 MySQL二:库操作 MySQL三:存储引擎 MySQL四:表操作 MySQL五:数据操作 MySQL六:索引原理与慢查询优化 MySQL七:数据备份 MySQL八:视图.触 ...
- 【合集】TiDB 源码阅读系列文章
[合集]TiDB 源码阅读系列文章 (一)序 (二)初识 TiDB 源码 (三)SQL 的一生 (四)INSERT 语句概览 (五)TiDB SQL Parser 的实现 (六)Select 语句概览 ...
- 学渣乱搞系列之Tarjan模板合集
学渣乱搞系列之Tarjan模板合集 by 狂徒归来 一.求强连通子图 #include <iostream> #include <cstdio> #include <cs ...
随机推荐
- token验证机制
最近在vue-cli项目实现登录的过程中用到了token验证,在此总结如下 1. 登录时,客户端通过用户名与密码请求登录 2. 服务端收到请求去验证用户名与密码 3. 验证通过,服务端会签发一个Tok ...
- STM32F407VET6之IAR之ewarm7.80.4工程建立（基于官方固件库1.6版本）
今天把stm32F407的工程之IAR建立完成了,特此记录下. 下载官方固件库,STM32F4xx_DSP_StdPeriph_Lib_V1.6.1,V1.8.0版本的同理.新建以下几个文件 src放 ...
- 稀疏表（ST / Sparse Table）
RMQ问题: 给定一个序列,每次询问一个区间最小值 / 最大值. 没有修改. //拿区间最大值来举例. memset(ans, -INF, sizeof(ans)); for (int i = 1; ...
- 使用html+javascriptt实现的简易四则运算（初学JavaScript笔记）
今天第一天学javascript,做了个简易的四则运算,提供参考,效果图: html代码: <!DOCTYPE html> <html > <head > < ...
- SMP IRQ Affinity
转:非常有用的方法,调式神器 SMP IRQ Affinity Background: Whenever a piece of hardware, such as disk controller or ...
- Mime类型与文件后缀对照表及探测文件MIME的方法
说明:刚刚写了一篇<IHttpHandler的妙用(2):防盗链!我的资源只有我的用户才能下载>的文章,网址:http://blog.csdn.net/zhoufoxcn/archive/ ...
- Leetcode26--->Remove Duplicates from Sorted Array(从排序数组中移除相同的元素)
题目: 给定一个排序数组,移除重复出现的元素,保证每个元素最终在数组中只出现一次.返回新数组的长度length; 要求:不能分配额外的一个数组使用,必须使用原地排序的思想,且空间复杂度为O(1) 举例 ...
- python 查看异常
接触python 一直觉着编译后报错经常没能捕捉显示,每次也只能从头看到尾 恰好在水木社区中看到关于异常捕捉帖子 方法一:捕获所有异常 try: a=b b=c except Exception,ex ...
- 使用Gson解析JSON数据
本文使用gson对json进行解析处理 首先,下载gson包 ,本文使用(gson-1.6.jar) package com.whroid.java.json; import com.google.g ...
- 性能测试之七--jdbc
jdbs用任意协议打开都行,具体脚本见下 在vuser_init里面 #include "Ptt_Mysql.h" vuser_init() { lr_load_dll (&quo ...