.NET 下二维码解决方案

使用Zint和Zxing实现二维码的编码与解码（Using open-source tools to generate and decode Q-R code）

1.Zint生成二维码

http://sourceforge.net/projects/zint/

【1】从上述站点下载Zint工具

【2】安装Zint工具

【3】使用Zint工具生成二维码，注意选择类型，并输入要生成的文本，此处我输入的是Hello World,Everyone!

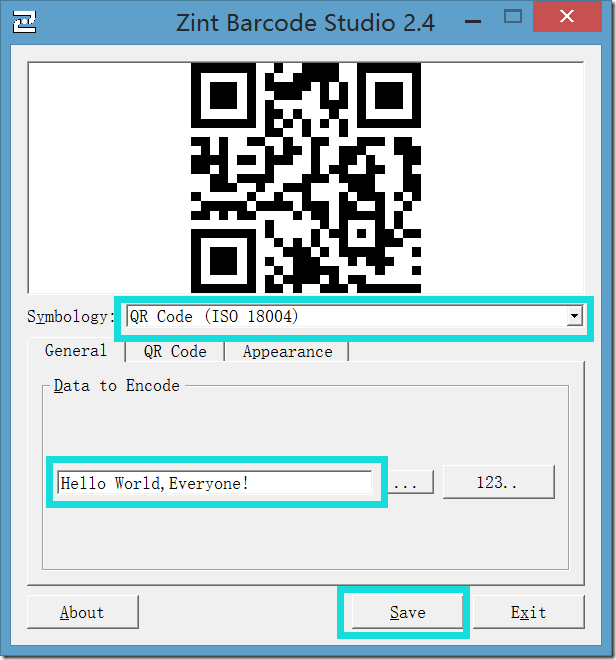
【4】保存Q-R二维码图像

这样我们的Q-R二维码图像就保存成功了【保存为hello.png】。

2.使用Zxing进行解码

Zxing是大名鼎鼎的条码处理开源项目，提供了多个平台上各种标准条形码的生成与解码工具。

https://github.com/zxing

Zxing提供了Android,Java,IPhone,Objective-C,C++,Jruby,Qt, .NET等各个平台库，其内容十分庞大，这里就不主要介绍了。下面，我们利用Zxing提供的JRuby项目进行简单的解码操作，把刚才生成的二维码图片作为输入，看看能否得到预期的输出。

【1】安装JRuby

由于Zxing原生于Java，因此它提供的库是JRuby版本的，于是先安装JRuby。（之所以选用JRuby是因为它比较轻量级，简单好用）

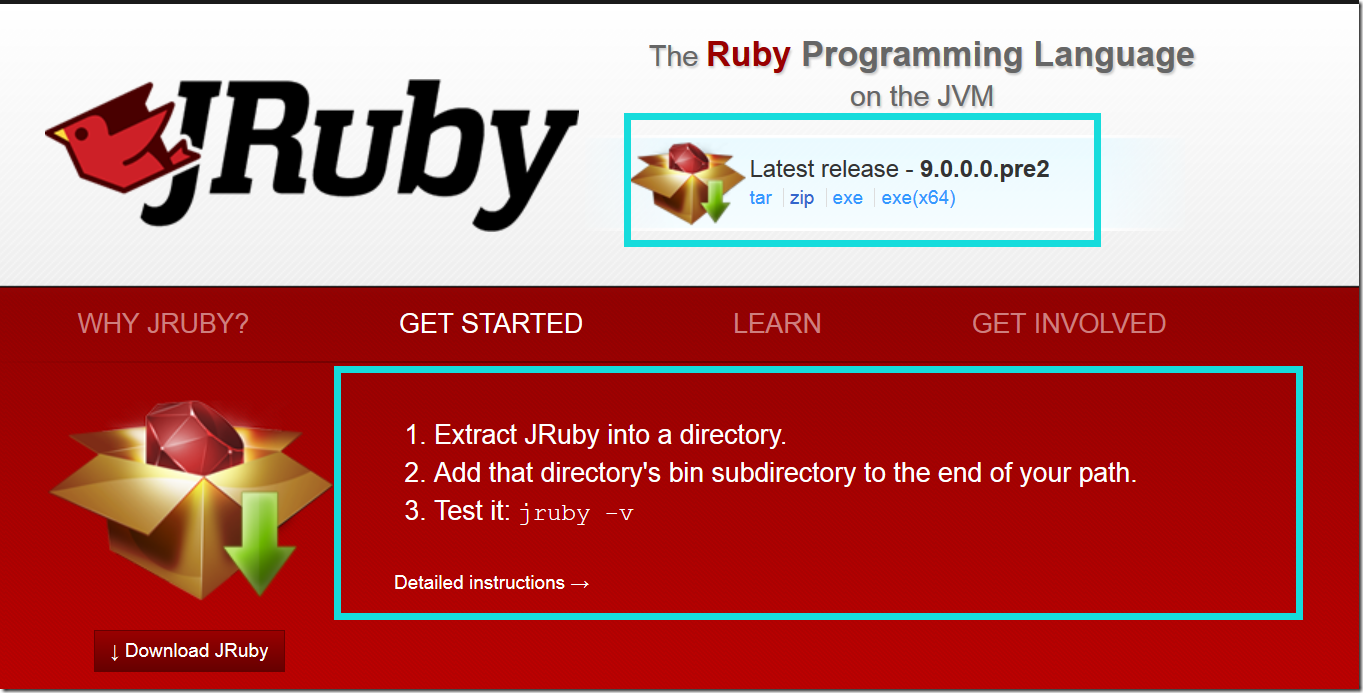
http://jruby.org/ 安装JRuby非常简单，只需3步：

（1）下载Jruby zip包

（2）解压JRuby

（3）将Jruby下bin目录所在路径加入PATH环境变量

（4）完成（在cmd中输入jruby -v测试是否安装成功）

【2】安装Zxing for ruby

https://github.com/ecin/zxing.rb

打开cmd，输入jruby -S gem install zxing等待数秒，jruby会为我们装好zxing。此时，我们就可以在ruby代码中import zxing了！

【3】编写解码程序

解码程序非常简单，在刚才保存图片的文件夹下新建一个ruby文件【1.ruby】,程序代码只需3行：

1 require 'zxing'

2

3 result = ZXing.decode 'hello.png'

4

5 puts result

简单的说，就是调用Zxing中的decode方法，输入参数为同目录下的“hello.png"文件，并将输入保存在result中。

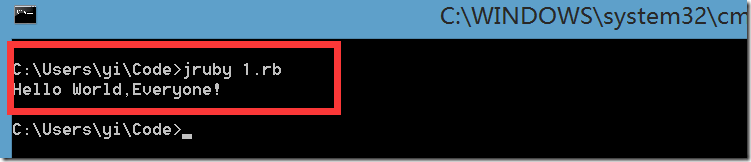
【4】执行解码程序

打开cmd，执行jruby 1.rb,其输出结果果然和我们输入时相同。

3.基于.NET的简单编解码工具

【1】下载Zxing.NET工具

http://zxingnet.codeplex.com/releases/view/117068

下载后，将其解压到任意位置，我们之后会用到其中的dll文件。

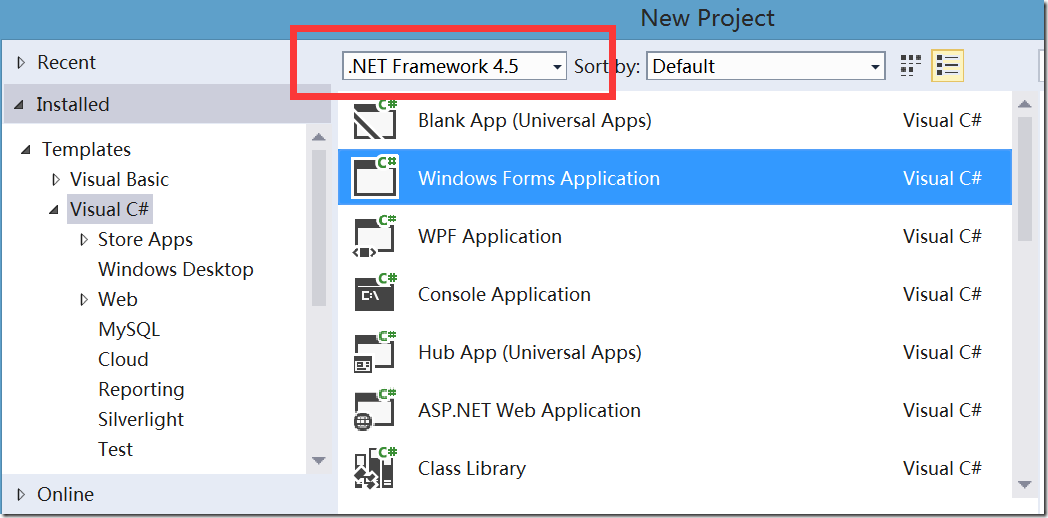
【2】在VS2013中建立winForm应用程序

【3】添加引用

添加引用时，请注意对应版本！！！选择对应版本的zxing.dll，将其加入到引用当中。

【4】设计GUI界面

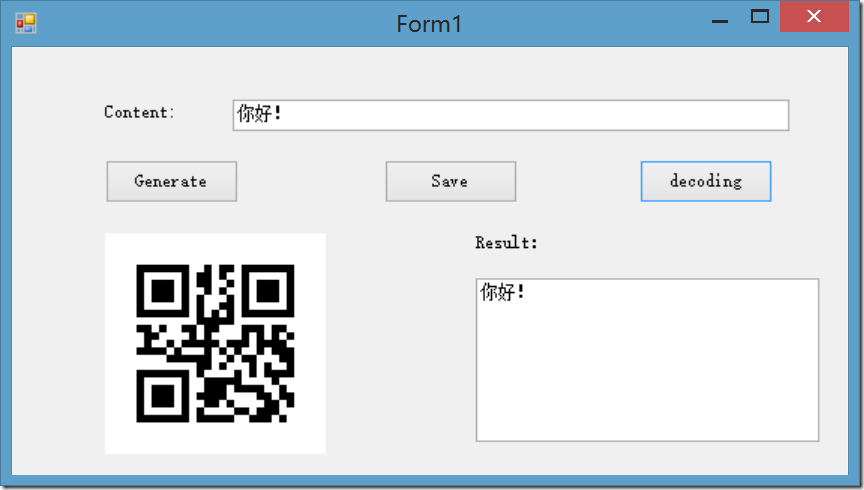
这里就展示一下，详细请下载工程代码（附件）

（1）输入文本，点击Generate，生成QR-Code

（2）点击Save，选择路径，保存QR-Code

（3）点击Decoding，选择相应的QR-Code文件，解码QR-Code，并将文本显示在Result中！

【5】编码

核心代码1：生成QR-Code

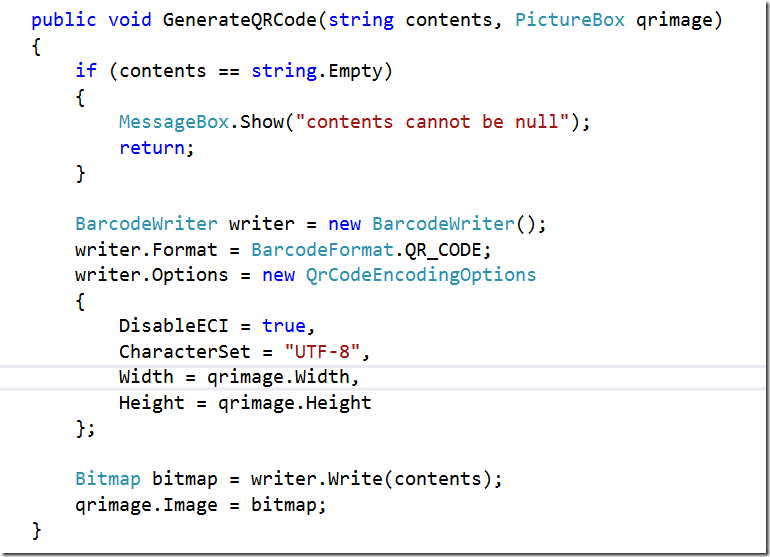
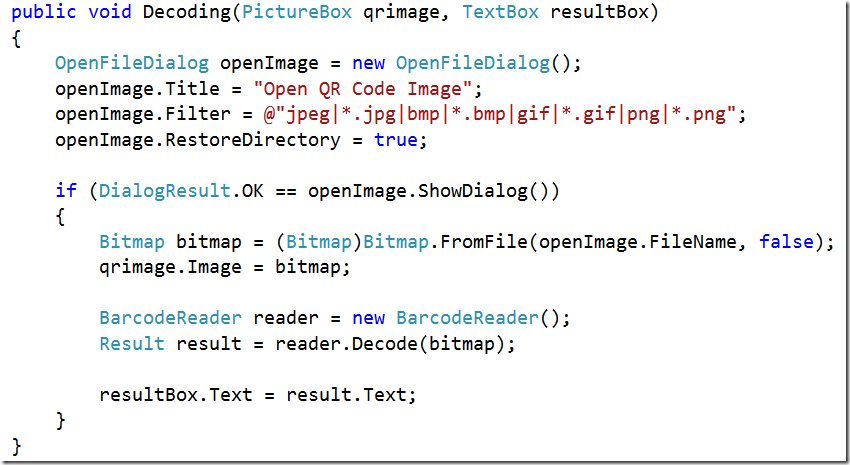
核心代码2：解码QR-Code

【6】功能展示

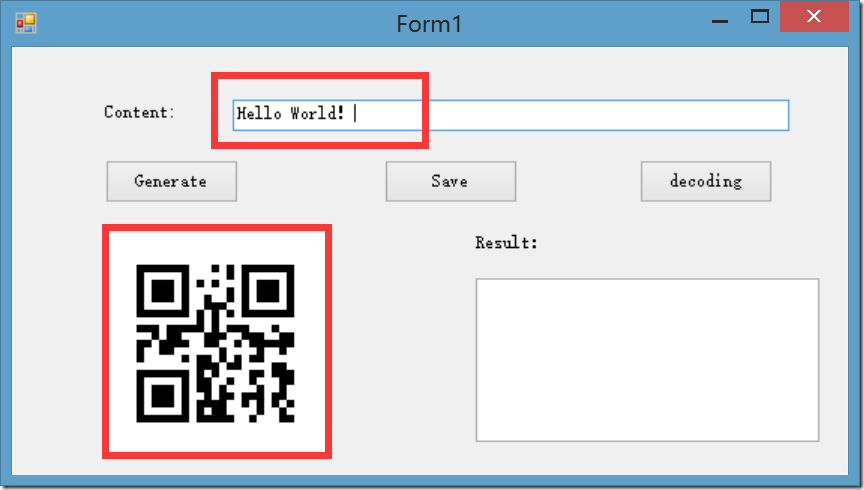
（1）生成QR-Code

输入Hello World！点击Generate！

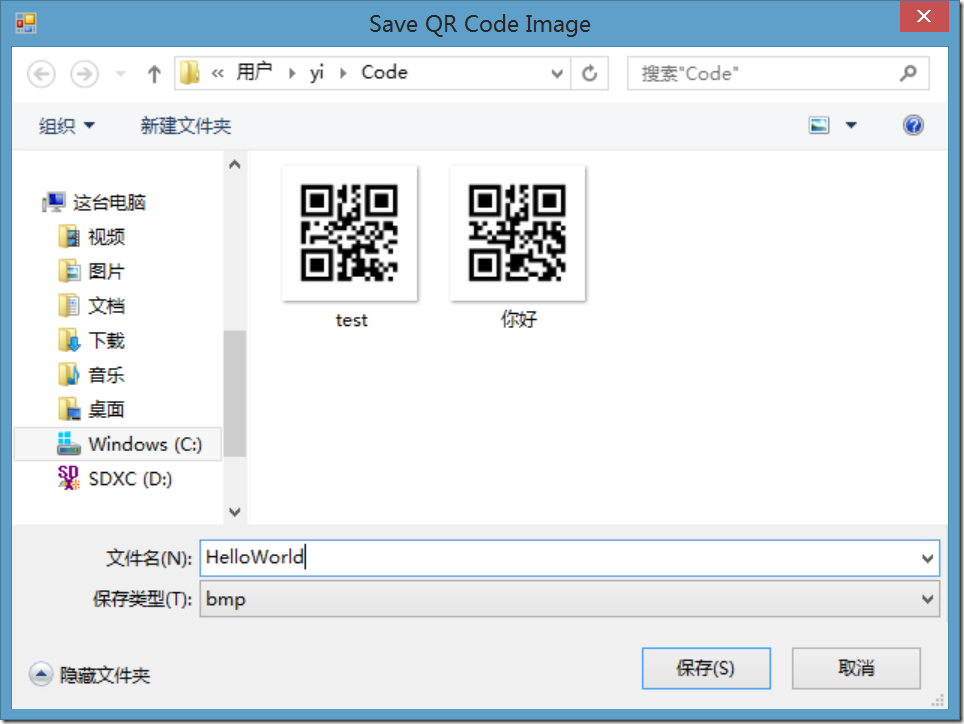
（2）保存QR-Code

（3）解码QR-Code

这次我们选择最开始我们利用Zint生成的hello.png，看看能否获得同样的结果。

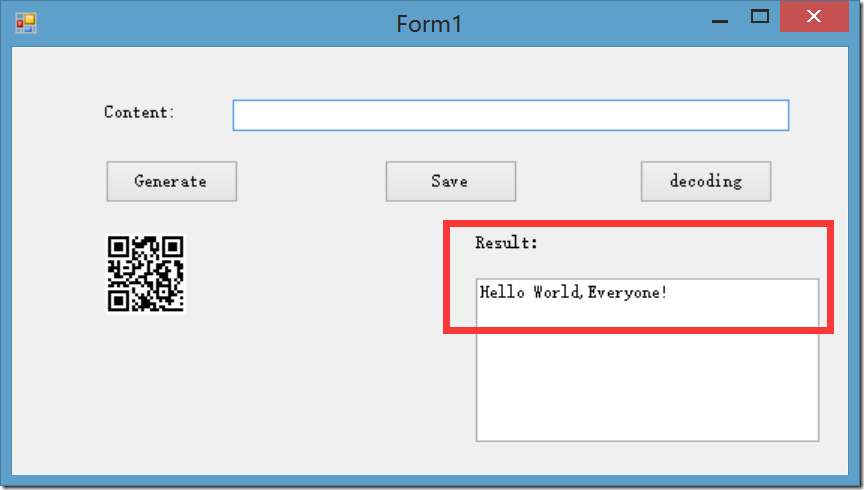
我们看到，结果与JRuby输出的结果相同。

【7】最后项目源码分享，欢迎进一步探讨，Thank you for your support！

Click me to get code.

转载自：http://www.cnblogs.com/Kassadin/p/4534952.html