luogu P4145 上帝造题的七分钟2 / 花神游历各国 维护区间和&&区间开根号

因为开根号能使数字减小得非常快

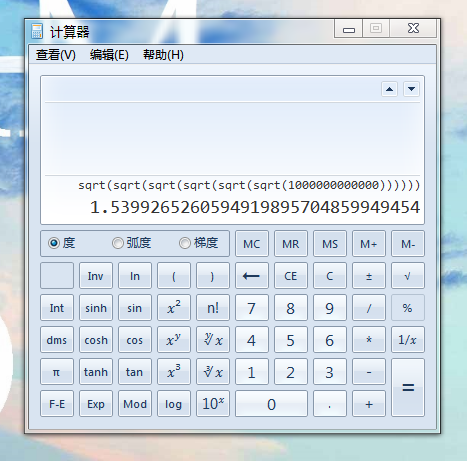
所以开不了几次（6次?）很大的数就会变成1.....

所以我们可以维护区间最大值，若最大值>1,则继续递归子树，暴力修改叶节点，否则直接return

（好像也可以维护区间被开方的次数，但我不会。。。QAQ）

#include<cstdio>
#include<iostream>
#include<cmath>
#define int long long
#define R register int
#define ls (tr<<1)
#define rs (tr<<1|1)
using namespace std;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
int n,m;
int mx[],sum[];
inline void build(int tr,int l,int r){
    if(l==r) {mx[tr]=sum[tr]=g(); return ;}
    R md=(l+r)>>;
    build(ls,l,md),build(rs,md+,r);
    mx[tr]=max(mx[ls],mx[rs]);
    sum[tr]=sum[ls]+sum[rs];
}
inline void calc(int tr,int l,int r,int ll,int rr) {
    if(mx[tr]<=) return ;
    if(l==r) {mx[tr]=sqrt(mx[tr]),sum[tr]=sqrt(sum[tr]); return ;}
    R md=(l+r)>>;
    if(ll>md) calc(rs,md+,r,ll,rr);
    else if(rr<md+) calc(ls,l,md,ll,rr);
    else calc(ls,l,md,ll,md),calc(rs,md+,r,md+,rr);
    mx[tr]=max(mx[ls],mx[rs]);
    sum[tr]=sum[ls]+sum[rs];
}
inline int query(int tr,int l,int r,int ll,int rr) {
    if(l==ll&&r==rr) return sum[tr];
    R md=(l+r)>>;
    if(ll>md) return query(rs,md+,r,ll,rr);
    else if(rr<md+) return query(ls,l,md,ll,rr);
    else return query(ls,l,md,ll,md)+query(rs,md+,r,md+,rr);
}
signed main() {
    n=g(); build(,,n); m=g();
    for(R i=,k,l,r;i<=m;++i) {
        k=g(),l=g(),r=g();
        if(l>r) swap(l,r);
        if(k&) printf("%lld\n",query(,,n,l,r));
        else calc(,,n,l,r);
    }
}

upd 2019.06.15

可以用树状数组做，如果这个数已经为$1$就用并查集合并到上一个位置，对于没有被开成$1$的直接暴力开根。。

跑的飞快

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<vector>
#include<queue>
#include<map>
#include<set>
#define ull unsigned long long
#define ll long long
#define R register ll
#define pause (for(R i=1;i<=10000000000;++i))
#define OUT freopen("out.out","w",stdout);
using namespace std;
namespace Fread {
    static char B[<<],*S=B,*D=B;
    #define getchar() (S==D&&(D=(S=B)+fread(B,1,1<<15,stdin),S==D)?EOF:*S++)
    inline ll g() {
        R ret=,fix=; register char ch; whaile(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
        do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
    } inline bool isempty(const char& ch) {return ch<=||ch>=;}
    inline void gs(char* s) {register char ch; while(isempty(ch=getchar())); do *s++=ch; while(!isempty(ch=getchar()));}
}using Fread::g; using Fread::gs;
const int N=; int n,m,fa[N];
ll c[N],h[N]; bool flg[N];
inline int lbt(int x) {return x&-x;}
inline void change(int pos) { R tmp=h[pos];
    h[pos]=sqrt(h[pos]); R d=tmp-h[pos];
    if(h[pos]==) flg[pos]=true;
    for(;pos<=n;pos+=lbt(pos)) c[pos]-=d;
}
inline ll query(int pos) { R ret=;
    for(;pos;pos-=lbt(pos)) ret+=c[pos]; return ret;
}
inline int getf(int x) {return (!flg[fa[x]])?fa[x]:fa[x]=getf(fa[x]);}
signed main() {
    n=g(); for(R i=;i<=n;++i) h[i]=c[i]=g(); for(R i=;i<=n;++i) fa[i]=i-;
    for(R i=;i<=n;++i) if(i+lbt(i)<=n) c[i+lbt(i)]+=c[i];
    m=g(); for(R i=,x,l,r;i<=m;++i) { x=g(),l=g(),r=g(); l>r?swap(l,r):void();
        if(x&) printf("%lld\n",query(r)-query(l-));
        else for(flg[r]?r=getf(r):;r>=l;r=getf(r)) change(r);
    }
}

---

2019.04.11&&2019.06.15