NOIP提高组初赛难题总结

注:笔者开始写本文章时noip初赛新题型还未公布，故会含有一些比较老的内容，敬请谅解.

约定:

若无特殊说明，本文中未知数均为整数
[表达式] 表示：在表达式成立时它的值为1,否则值为0
x!表示x的阶乘
整数除法无特殊说明，默认下取整

阅读程序

1.[NOIP2018]提高组阅读程序3

#include <cstdio>
using namespace std;
const int N = 110;
bool isUse[N];
int n, t;
int a[N], b[N];
bool isSmall(){
    for (int i = 1; i <= n; ++i)
    if (a[i] != b[i]) return a[i] < b[i];
    return false;
}
bool getPermutation(int pos){
    if (pos > n){
        return isSmall();
    }
    for (int i = 1; i <= n; ++i){
        if (!isUse[i]){
            b[pos] = i; isUse[i] = true;
            if (getPermutation(pos + 1)){
                return true;
            }
            isUse[i] = false;
        }
    }
    return false;
}
void getNext(){
    for (int i = 1; i <= n; ++i){
        isUse[i] = false;
    }
    getPermutation(1);
    for (int i = 1; i <= n; ++i){
        a[i] = b[i];
    }
}
int main(){
    scanf("%d%d", &n, &t);
    for (int i = 1; i <= n; ++i){
        scanf("%d", &a[i]);
    }
    for (int i = 1; i <= t; ++i){
        getNext();
    }
    for (int i = 1; i <= n; ++i){
        printf("%d", a[i]);
        if (i == n) putchar('\n'); else putchar(' ');
    }
    return 0;
}
输入1：6 10 1 6 4 5 3 2
输入2：6 200 1 5 3 4 2 6

答案:

输出1：2 1 3 5 6 4
输出2：3 2 5 6 1 4

分析:

首先我们看出，这是求

第一问可以直接模拟，第二问直接模拟循环次数太多，可以用康托展开求解。先介绍一下康托展开:

知识点补充:康托展开

康托展开:把全排列按字典序排序，给出一个长度为n的全排列，求它是第几个长度为n的全排列。

我们以1 5 3 4 2 6 为例,先求字典序比它小的全排列有多少个

第1位是1,没有第一位比它小的全排列
第2位是5,后面的位里比它小的有2,3,那么以2,3作为第二位的全排列一定比它的字典序小。又因为第1位就小的全排列已经算过了,我们只需要算第1位为1,第2位为2或3的全排列数量。第1位固定，第2位2种排法后面4位可以任意排，有4!种。故答案为2*4!
第3位是3,后面比它小的有2,根据上一问的结论，答案为1*3!
第4位是4,后面比它小的有2,同理答案为1*2!
第5位是2,后面没有比它小的数,答案为0*1!
由于前5位已经确定，可以直接推出第6位，所以这一位不用考虑，为0
比它小的排列有$2*4!+1*3!+1*2!+0*1!=80$个，所以它是第81个排列

综上，我们可以给出康托展开的公式.给出一个长度为n的序列$a$，$a$在排列中的个数为

\[\sum_{i=1}^n f(i)\times(n-i)! \\ f(i)=\sum_{j=i+1}^n[a_j<a_i],即i后面比a_i小的数的个数
\]

逆康托展开:把全排列按字典序排序，求长度为n的全排列中,第k个全排列

我们以k=281,n=6为例。

我们求小于它的排列的个数，即281-1=280.设S表示当前还未确定位置的数的集合。初始时S={1,2,3,4,5,6}
$280/5!=2\cdots\cdots40$,S={1,2,3,4,5,6}那么我们要找S集合中小于它的数有2个的数，即S集合中的第3个数3. 那么排列的第1位为3,把3移出S
$40/4!=1\cdots\cdots16$,S={1,2,4,5,6},同理，排列的第2位为S集合中的第1+1个数2,
$16/3!=2 \dots \dots 4$,S={1,4,5,6},排列的第3位为5
$4/2!=2 \cdots \cdots 0$,S={1,4,6},排列的第4位为6
$0/1!=1 \cdots \cdots 0$,S={1,4} 排列的第5为为1
最后一位就是S集合中剩下的那个数，为4
综上，排列为3 2 5 6 1 4

那么对于这道题，我们只需要先对1 5 3 4 2 6做康托展开，加上200，再逆康托展开即可

2.[NOIP2017]普及组阅读程序4

#include<iostream>
using namespacestd;
int main() {
    int n, m;
    cin >> n >> m;
    int x = 1;
    int y = 1;
    int dx = 1;
    int dy = 1;
    int cnt = 0;
    while (cnt != 2) {
        cnt = 0;
        x = x + dx;
        y = y + dy;
        if (x == 1 || x == n) {
            ++cnt;
            dx = -dx;
        }
        if (y == 1 || y == m) {
            ++cnt;
            dy = -dy;
        }
    }
    cout << x << " " << y<< endl;
    return 0;
}
输入1: 4 3
输入2: 2017 1014

答案:

输出1: 1 3
输出2: 2017 1

分析:

同样也是第1问模拟，第二问找规律。

发现$x,y$坐标的移动可以分离来考虑。x相当于长度为n-1的线段上的一个动点，从坐标1出发到坐标n不停往返。y相当于长度为m-1的线段上的一个动点，从1出发到m不停往返。两动点的速度相等.当某个时刻，两动点同时到达边界(坐标1或n,m)的时候结束.

容易发现，相遇的时候走的距离为为$s=\mathrm{lcm} (n-1,m-1)$

以从1到n或从n到1为走了一次，那么x走了$\frac{s}{n-1}$次,y走了$\frac{s}{m-1}$次。当$\frac{s}{m-1}$为偶数时恰好回到起点，输出1.否则输出n(或m）.

以$n=2017,m=1014$为例,$n-1=2016,m-1=1013,s=2016$,$s/(n-1)=1$,为奇数，因此输出2017.$s/(m-1)=2$为偶数,因此输出1

问题求解

小陈现有2个任务A,B要完成,每个任务分别有若干步骤如下：A=a1->a2->a3,B=b1->b2->b3->b4->b5.在任何时候,小陈只能专心做某个任务的一个步骤.但是如果愿意,他可以在做完手中任务的当前步骤后,切换至另一个任务,从上次此任务第一个未做的步骤继续.每个任务的步骤顺序不能打乱,例如……a2->b2->a3->b3……是合法的,而……a2->b3->a3->b2……是不合法的.小陈从B任务的b1步骤开始做,当恰做完某个任务的某个步骤后,就停工回家吃饭了.当他回来时,只记得自己已经完成了整个任务A,其他的都忘了.试计算小陈饭前已做的可能的任务步骤序列共有多少种.

答案：70

首先因为第一个做b1,完成了a.我们先构建原始的序列b1->a1->a2->a3,然后再把b2->b3->b4->b4中的几个插进去，保证这几个顺序递增。可以插在b1后的4个空里。

因为必须要按顺序插进去，我们可以把b2,b3,b4看成无标号的来求方案数。相当于把m个球放到n个位置上，每个位置的球数>=0.根据插板法，答案是$C_{n+m-1}^{n-1}=C_{n+m-1}^m$,此题中$n=4$,所以$C_{m+3}^m$

最终答案是$\sum_{m=1}^4 C_{m+3}^m=70$

现有一只青蛙，初始时在 n 号荷叶上。当它某一时刻在 k 号荷叶上时，下一时刻将等概率地随机跳到 1, 2, …, k 号荷叶之一上，直至跳到 1 号荷叶为止。当 n = 2 时，平均一共跳 2 次；当 n = 3 时，平均一共跳 2.5 次。则当 n = 5 时，平均一共跳几次。

答案：$\frac{37}{12}$

其实就是期望跳的次数.设$f_i$表示已经跳到i号荷叶，期望跳到1号荷叶的次数。

那么$f_1=0$

$f_2=\frac{1}{2}(f_1+f_2)+1$.因为在2号荷叶，下一步跳到1和2的概率均为1/2,根据期望的线性性。答案就是1和2荷叶跳到终点的期望次数之和乘1/2，再加上1步。因为$f_1$已知，可以解出$f_2=2$

同理有

$f_3=\frac{1}{3}{(f_1+f_2+f_3)}+1$

$f_4=\frac{1}{4}{(f_1+f_2+f_3+f_4)}+1$

$f_5=\frac{1}{5}{(f_1+f_2+f_3+f_4+f_5)}+1$

最终可以解出$f_5=\frac{37}{12}$

将2006 个人分成若干不相交的子集,每个子集至少有 3 个人,并且:

(1)在每个子集中,没有人认识该子集的所有人.

(2)同一子集的任何 3 个人中,至少有 2 个人互不认识.

(3)对同一子集中任何 2 个不相识的人,在该子集中恰好只有 1 个人认识这两个人.则满足上述条件的子集最多能有___________个

答案：401

转化成图论。每个人看成点，每个相识关系看作一条边。那么条件就变成了。

没有一个结点与其他所有点相连
每个子集中,任何三个结点中,至少两个不相连
同一子集中的任意不直接相连的两点,彼此之间有只通过一个结点的路径

然后尝试从小到大枚举每个子集的点数和边数。发现5个点时，连成一个五边形恰好满足条件。那么每5个人分一组，答案就是401.

从 1 到 2018 这 2018 个数中，共有__个包含数字8的数

答案:544

因为可能包含多个数字8，容易算重。考虑补集转化，求不包含数字8的数字个数。

一位数：8个

两位数：$8 \times 9 $个

三位数：$8 \times 9 \times 9$个

四位数,[1000,1999]之内的:$1\times 8 \times 9 \times 9$个

四位数,[2000,2018]内的,2008,2018两个

以上一共是1474个。答案为：2018-1474=544个

某个国家的钱币面值有1，7，7^2，73共计四种，如果要用现金付清10015元的货物，假设买卖双方各种钱币的数量无限且允许找零，那么交易过程中至少需要流通______张钱币。

答案:35

首先我们应该优先用面值尽量大的

$10015/343=29 \dots \dots 68$,所以用29张7^3的

$68 /49 =1 \dots 19$,所以用1张7^2的

19可以用2张7元+5张1元凑出，但是这样不如给对方3张7元再找回2张1元，只需要5张货币。

总共29+1+5=35

书架上有21本书，编号从1 到 21 从中选4 本，其中每两本的编号都不相邻的选法一共有__种

答案:3060

反着考虑，先放好另外17本书，再把4本插进去.18个空选4个，答案是$C_{18}^4=3060$

一个人站在坐标(0, 0)处，面朝x轴正方向。第一轮，他向前走1单位距离，然后右转；第二轮，他向前走2单位距离，然后右转；第三轮，他向前走3单位距离，然后右转......他一直这么走下去。请问第2017轮后，他的坐标是__

答案:(1009,1008)

找规律:第1步，X轴+1，第2步，Y轴-2，第3步X轴-3，第4步，Y轴+4，第5步，X轴+5，...，(x轴每变化4次都为0)

假设走的步数为n，$n \ \mathrm{mod}\ 4 $余1是X轴+n，余2是Y轴-n，余3是X轴-n，余0是Y轴+n，2017%4=1，2016%4=0，

所以x轴是1-3+5-7+9...+2017=1-3+5-7+9...-2015+2017=1009，*

y轴是-2+4-6+8-10...+2016=1008。所以最终坐标是（1009，1008）

由五个不同的节点构成的树有（）种

答案:125

知识点补充:Prufer序列

Prufer序列，可以用来求解无根树计数的问题。

(1)无根树转化为 Prufer 序列。

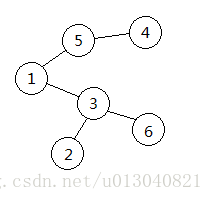
找到编号最小的叶子节点(度数为1)并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。

如下图的树对应的 Prufer序列就是3,5,1,3。

（2）Prufer序列转化为无根树。

设点集 S={1,2,3,...,n}，每次取出 Prufer 序列中最前面的元素u，在S中找到编号最小的没有在 Prufer 序列中出现的元素v，连边(u,v),并在Prufer序列中删掉u,v，最后在 S 中剩下两个节点，给它们连边。最终得到的就是无根树。

常用结论:

1.一个n个点的有标号无根树唯一对应一个长度为n-2的Prufer序列

2.$n$个点的有标号无根树有$n^{n-2}$个

根据第1个结论，第2个结论显然成立

3.**Prufer 序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1 **

每个非叶子节点编号的出现次数就是它的儿子个数，即度数-1

4.$n$个节点的度依次为$d_1,d_2,d_3 \dots d_n$的有标号无根树的个数为:

\[\begin{aligned} \frac{(n-2)!}{(d_1-1)(d_2-1)(d_3-1) \cdots (d_n-1)} \end{aligned}
\]

根据第3个结论,此时prufer序列中编号i出现了$d_i-1$次,那么就是一个长度为n-2的可重排列

回到上述题目

由五个不同的节点构成的树有（）种

$n=5,n^{n-2}=125$

选择题

知识点补充:特征根方程

给出一个数列$f$满足递推式$f_n=pf_{n-1}+qf_{n-2},f_1=a,f_2=b$,求它的通项公式.

递推式的通项不好求，但是等比数列的通项很好求.假如等比数列$\{g_n\}$满足递推式,就可以快速求出通项了。

另外我们还可以得到一个结论:

已知等比数列$\{a_n\},\{b_n\},\{c_n\} \cdots$,那么它们的线性组合$\{\alpha \cdot a_n + \beta \cdot b_n + \gamma \cdot c_n\cdots\}$也满足递推式。

那么考虑如何构造这个等比数列${g_n}$.

设$g_n=x^{n-1}$(写n-1是因为后面解二元一次方程比较方便),带入原递推式,那么$x^{n-1}=px^{n-2}+qx^{n-3}$,

\[x^2 = px+q \\ x^2-px-q =0
\]

\[x_1,x_2=\frac{p \pm \sqrt{p^2+4q}}{2}
\]

那么${g_{1}}_{n}=x_1^{n-1},{g_{2}}_{n} =x_2^{n-1}$都满足递推式，根据前面的结论，$f_n=\alpha x_1^{n-1}+\beta x_2^{n-1}$就是$f$的通项公式

$\alpha,\beta$如何确定?因为$f_1=a,f_2=b$，代入可知$$\begin{cases} \alpha+\beta=a \ \alpha x_1+ \beta x_2=b \end{cases}$$

解这个方程，就可以确定$\alpha,\beta$

知识点补充:时间复杂度分析

这个的孙题比较多，还是讲一下比较好

upd:没想到这一咕咕到了复赛后,还是推荐一下巨佬的博客吧