POJ 3743 LL’s cake（圆+PSLG）

题意是给你一块在原点半径为10的圆，然后告诉你一条直线在圆弧上的极角，相当于用这条直线把这个圆分成两半，然后一共是n条直线切圆，就好比切蛋糕，问你其中最大一块的面积是多少。

如果我们将圆弧转化成直线边，那么这个题就变成PSLG裸题，但是这里是圆弧，所以我们需要将其转化。

我先将所有在圆上的点记录下来，最后极角排序，绕一周，这些点分割出来肯定会有一部分算面积的时候是要算上那部分弓型面积，但是有一部分不是，主要是这部分面积仅仅就是这块弓型面积，没有其他多边形面积，例如样例3，为了避免这种问题，我们可以直接在相邻两点之间塞入一个点，在进行连边，那么相当于我们给仅仅只有弓型区域内的点一个三角形面积，这样主要保证的是在跑PSLG的时候可以把这块面积算进去，因为每条边只算两次，但是如果是仅仅只有弓型面积所在的那条边，本来应该逆时针绕一圈算面积，所以这样就会有问题。

C++提交正确 G++wa惨？？？

这样就会有问题

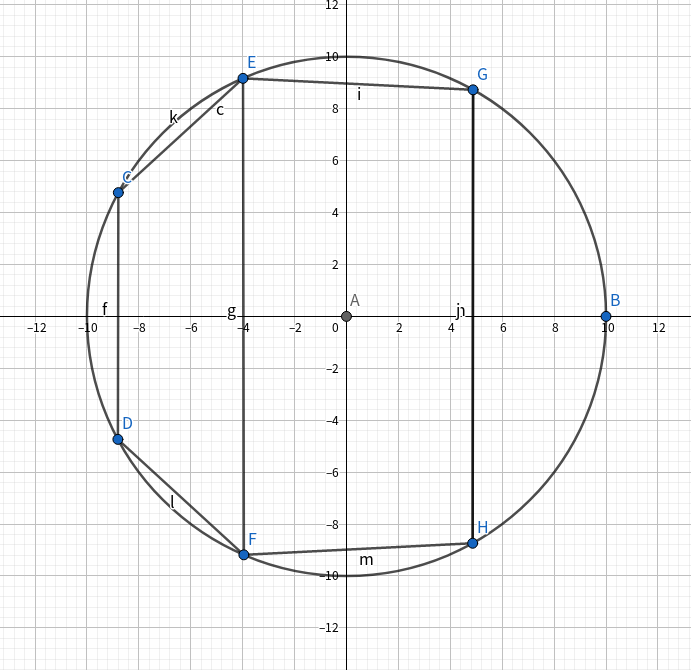
这样建边就没有大问题了

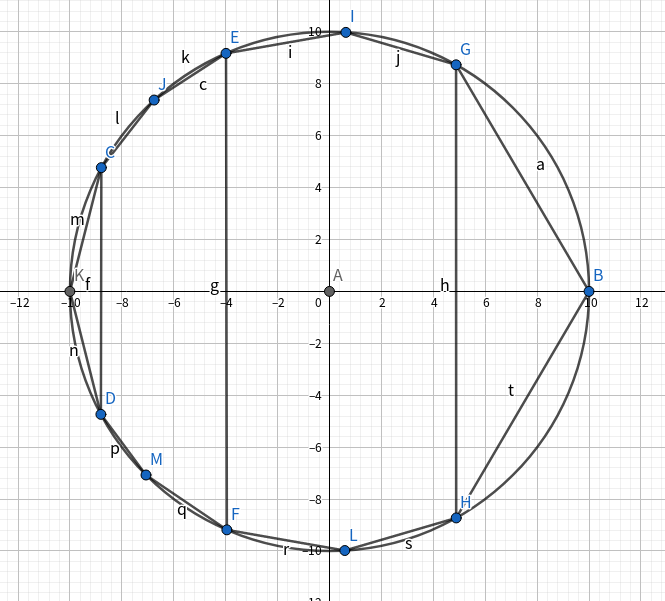
 //      ——By DD_BOND

 //#include<bits/stdc++.h>
 //#include<unordered_map>
 //#include<unordered_set>
 #include<functional>
 #include<algorithm>
 #include<iostream>
 //#include<ext/rope>
 #include<iomanip>
 #include<climits>
 #include<cstring>
 #include<cstdlib>
 #include<cstddef>
 #include<cstdio>
 #include<memory>
 #include<vector>
 #include<cctype>
 #include<string>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<ctime>
 #include<stack>
 #include<map>
 #include<set>

 #define fi first
 #define se second
 #define pb push_back
 #define MP make_pair

 using namespace std;

 typedef double db;
 typedef long long ll;
 typedef pair<db,db> Pd;
 typedef pair<int,int> P;
 typedef pair<ll,ll> Pll;

 const db eps=1e-;
 const int MAXN=1e5+;
 const db pi=acos(-1.0);
 const ll INF=0x3f3f3f3f3f3f3f3f;

 inline int dcmp(db x){
     if(fabs(x)<eps) return ;
     return (x>? : -);
 }

 inline db Sqrt(db x){
     return x>? sqrt(x): ;
 }

 inline db sqr(db x){ return x*x; }

 struct Point{
     db x,y; int id,nx;
     Point(){ x=,y=; }
     Point(db _x,db _y):x(_x),y(_y){}
     void input(){
         double _x,_y;
         scanf("%lf%lf",&_x,&_y);
         x=_x,y=_y;
     }
     void output(){ printf("%.4f %.4f\n",(double)x,(double)y); }
     bool operator ==(const Point &b)const{
         return (dcmp(x-b.x)==&&dcmp(y-b.y)==);
     }
     bool operator !=(const Point &b)const{
         return !((dcmp(x-b.x)==&&dcmp(y-b.y)==));
     }
     bool operator <(const Point &b)const{
         return (dcmp(x-b.x)==? dcmp(y-b.y)< : x<b.x);
     }
     db operator ^(const Point &b)const{     //叉积
         return x*b.y-y*b.x;
     }
     db operator *(const Point &b)const{     //点积
         return x*b.x+y*b.y;
     }
     Point operator +(const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator -(const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     Point operator *(db a){
         return Point(x*a,y*a);
     }
     Point operator /(db a){
         return Point(x/a,y/a);
     }
     db len2(){  //长度平方
         return sqr(x)+sqr(y);
     }
     db len(){   //长度
         return Sqrt(len2());
     }
     db polar(){ //向量的极角
         return atan2(y,x);   //返回与x轴正向夹角(-pi~pi]
     }
     Point rotate_left(){    //逆时针旋转90度
         return Point(-y,x);
     }
     Point rotate_right(){   //顺时针旋转90度
         return Point(y,-x);
     }
     Point rotate(Point p,db ang){   //绕点p逆时针旋转ang度
         Point v=(*this)-p;
         db c=cos(ang),s=sin(ang);
         return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
     }
 };

 inline db cross(Point a,Point b){   //叉积
     return a.x*b.y-a.y*b.x;
 }

 inline db dot(Point a,Point b){ //点积
     return a.x*b.x+a.y*b.y;
 }

 inline db dis(Point a,Point b){ //两点的距离
     Point p=b-a;    return p.len();
 }

 inline db rad(Point a,Point b){    //两个向量的夹角
     return fabs(atan2(fabs(cross(a,b)),dot(a,b)));
 }

 inline bool is_parallel(Point a,Point b){  //判断向量是否平行
     db p=rad(a,b);
     return dcmp(p)==||dcmp(p-pi)==;
 }

 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线
     Point operator &(const Line &b)const{    //求两直线交点
         Point res=s;
         db t=((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
         res.x+=(e.x-s.x)*t;
         res.y+=(e.y-s.y)*t;
         return res;
     }
 };

 inline int relation(Point p,Line l){   //点和向量关系   1:左侧   2:右侧   3:在线上
     int c=dcmp(cross(p-l.s,l.e-l.s));
     if(c<) return ;
     else if(c>)    return ;
     else    return ;
 }

 inline bool is_parallel(Line a,Line b){    //直线平行
     return is_parallel(a.e-a.s,b.e-b.s);
 }

 struct Circle{
     Point p;
     db r;
     Circle(){}
     Circle(Point _p,db _r):p(_p),r(_r){}
 };

 inline int relation(Point p,Circle a){ //点和圆的位置关系  0:圆外    1:圆上   2:圆内
     db d=dis(p,a.p);
     if(dcmp(d-a.r)==)  return ;
     return (dcmp(d-a.r)<? : );
 }

 inline db area_radian(db th,db r){ //返回半径为R,弧度为th的弓形面积
     return 0.5*r*r*(th-sin(th));
 }

 inline db polygon_area(vector<Point> p){    //多边形的有向面积，加上绝对值就是面积  正值表示输入点按照逆时针 否则为顺时针
     int n=p.size(); db area=;
     for(int i=;i<n-;i++)  area+=cross(p[i]-p[],p[i+]-p[]);
     area=fabs(area)/;
     for(int i=,j=;i<n;i++,j++){
         if(j==n)    j=;
         if(p[i].nx==p[j].id||p[j].nx==p[i].id)  area+=area_radian(rad(p[i],p[j]),);
     }
     return area;
 }

 struct Edge{
     int from,to;
     db ang;
     Edge(){ ang=from=to=; }
     Edge(int s,int t,db a){ from=s,to=t,ang=a; }
 };
 int n,m,face_cnt;   //平面个数 包括外面最大的多边形
 db area[MAXN];  //每个多边形面积
 Point point[MAXN];  //平面内所有的点
 vector<Edge>edge;
 vector<int>G[MAXN];
 vector<Point>polygon;
 vector<Point>face[MAXN];
 int vis[*MAXN],pre[*MAXN];   //left表示这条边的左侧属于哪个面
 inline void Init(){
     for(int i=;i<(int)edge.size();i++)  vis[i]=;
     edge.clear();
     for(int i=;i<n;i++)    G[i].clear();
     for(int i=;i<face_cnt;i++) face[i].clear();
     n=m=face_cnt=;
 }
 inline void AddEdge(int from, int to){             //需要建立反向边帮助寻找下一条边
     edge.pb(Edge(from,to,(point[to]-point[from]).polar()));
     edge.pb(Edge(to,from,(point[from]-point[to]).polar()));
     m=edge.size();
     G[from].pb(m-);
     G[to].pb(m-);
 }
 inline void Build(){
     for(int u=;u<n;u++){
         int d=G[u].size();
         for(int i=;i<d;i++)
             for(int j=i+;j<d;j++)
                 if(edge[G[u][i]].ang>edge[G[u][j]].ang)
                     swap(G[u][i],G[u][j]);
         for(int i=;i<d;i++)    pre[G[u][(i+)%d]]=G[u][i]; //从u出发的i条边顺时针旋转的第一条边是pre[i]
     }
     for(int u=;u<n;u++){
         for(int i=;i<(int)G[u].size();i++){
             int e=G[u][i];
             if(!vis[e]){
                 while(){
                     vis[e]=;
                     int from=edge[e].from;
                     polygon.pb(point[from]);
                     e=pre[e^];         //逆时针旋转最多的一条边即为顺时针转动的第一条边
                     if(e==G[u][i])  break;
                 }
                 face[face_cnt++]=polygon;
                 polygon.clear();
            }
         }
     }
     for(int i=;i<face_cnt;i++)  area[i]=polygon_area(face[i]);
 }

 typedef pair<Point,int> pdd;

 pdd st[MAXN];
 vector<pair<db,int> >tmp[MAXN];

 inline bool cmp(pdd x,pdd y){
     return x.fi.polar()<y.fi.polar();
 }

 inline void Insert(Line *line,int m){
     for(int i=;i<m;i++)
         for(int j=i+;j<m;j++)
             if(!is_parallel(line[i],line[j])){
                 Point inter=line[i]&line[j];
                 if(dcmp(inter.len()-)>)  continue;
                 point[n++]=inter;
             }
     sort(point,point+n);
     n=unique(point,point+n)-point;
     for(int i=;i<n;i++)    point[i].id=i;
     int cnt=;
     for(int i=;i<n;i++)
         if(dcmp(point[i].len()-)==)
             st[cnt++]=pdd(point[i],i);
     sort(st,st+cnt,cmp);
     st[cnt]=st[];
     for(int i=;i<cnt;i++)   st[i].fi.nx=st[i+].fi.id;
     for(int i=;i<cnt;i++)   point[st[i].se]=st[i].fi;
     for(int i=;i<m;i++){
         for(int j=;j<n;j++)
             if(relation(point[j],line[i])==)
                 tmp[i].pb(MP(dot(point[j]-line[i].s,line[i].e-line[i].s),j));
         sort(tmp[i].begin(),tmp[i].end());
         for(int j=;j<(int)tmp[i].size();j++)  AddEdge(tmp[i][j-].se,tmp[i][j].se);
     }
     for(int i=;i<m;i++)    tmp[i].clear();
     Build();
 }

 typedef pair<db,Point> pd;

 pd a[MAXN];
 Line line[MAXN];

 int main(void){
     int T;  scanf("%d",&T);
     while(T--){
         Init();
         int n,m=,k=;  scanf("%d",&n);
         for(int i=;i<n;i++){
             double x,y; scanf("%lf%lf",&x,&y);
             db s=x,t=y;
             Point p1=Point(*cos(s),*sin(s));
             Point p2=Point(*cos(t),*sin(t));
             a[k++]=pd(s,p1);
             a[k++]=pd(t,p2);
             line[m++]=Line(p1,p2);
         }
         sort(a,a+k);
         k=unique(a,a+k)-a;
         a[k]=a[];  a[k].fi+=*pi;
         for(int i=;i<k;i++){
             Point tmp;
             if(dcmp(a[i+].fi-a[i].fi-pi)==)   tmp=a[i].se.rotate_left();
             else if(dcmp(a[i+].fi-a[i].fi-pi)>){
                 tmp=a[i].se+a[i+].se;
                 tmp=tmp/tmp.len()*-;
             }
             else{
                 tmp=a[i].se+a[i+].se;
                 tmp=tmp/tmp.len()*;
             }
             line[m++]=Line(a[i].se,tmp);
             line[m++]=Line(tmp,a[i+].se);
         }
         Insert(line,m);
         sort(area,area+face_cnt);
         printf("%.2f\n",(double)area[face_cnt-]);
     }
     return ;
 }