洛谷P3943 星空

题目背景

命运偷走如果只留下结果， 时间偷走初衷只留下了苦衷。

你来过，然后你走后，只留下星空。

题目描述

逃不掉的那一天还是来了，小 F 看着夜空发呆。

天上空荡荡的，没有一颗星星——大概是因为天上吹不散的乌云吧。

心里吹不散的乌云，就让它在那里吧，反正也没有机会去改变什么了。

小 C 拿来了一长串星型小灯泡，假装是星星，递给小 F，想让小 F 开心一点。

不过，有着强迫症的小 F 发现，这串一共 n 个灯泡的灯泡串上有 k 个灯泡没有被点亮。

小 F 决定和小 C 一起把这个灯泡串全部点亮。

不过，也许是因为过于笨拙，小 F 只能将其中连续一段的灯泡状态给翻转——点亮暗灯泡，熄灭亮灯泡。

经过摸索，小 F 发现他一共能够翻转 m 种长度的灯泡段中灯泡的状态。

小 C 和小 F 最终花了很长很长很长很长很长很长的时间把所有灯泡给全部点亮了。

他们想知道他们是不是蠢了，因此他们找到了你，让你帮忙算算：在最优的情况下，至少需要几次操作才能把整个灯泡串给点亮？

输入输出格式

输入格式：

从标准输入中读入数据。

输入第 1 行三个正整数 n,k,m。

输入第 2 行 $k$ 个正整数，第 i 个数表示第 i 个被没点亮的灯泡的位置 $a_i$。

输入第 3 行 $m$ 个正整数，第 i 个数表示第 i 种操作的长度 $b_i$。

保证所有 $b_i$ 互不相同；保证对于 $1 \le i < k$，有 $a_i< a_{i+1}$；保证输入数据有解。

输出格式：

输出标准输入中。

输出一行一个非负整数，表示最少操作次数。

输入输出样例

输入样例：

输出样例：

说明

【样例 1 解释】

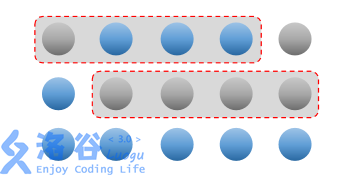
【数据范围与约定】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。

每个测试点的数据规模及特点如下表

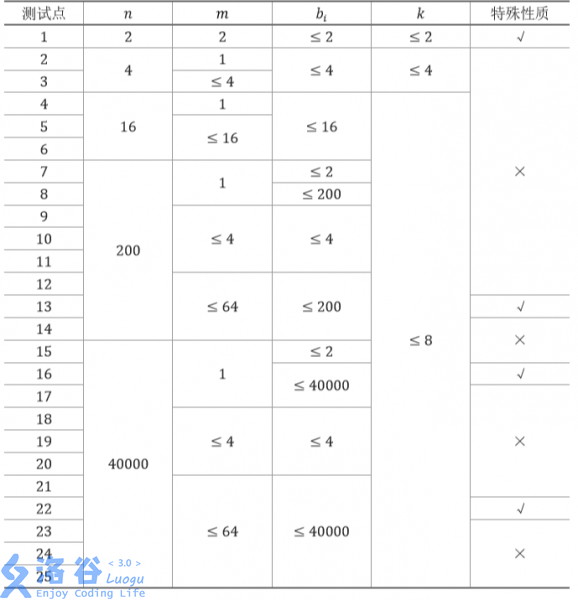
特殊性质：保证答案小于 4

题解Here!

一道状压$DP$好题。

首先发现$n$特别的大，但是$k$特别小，显然是要在$k$上面做文章。

注意到$k\leq8$，感觉有点状压$DP$的样子啊。

我们先对原序列进行异或差分。

异或差分是啥？$emmmm\cdots\cdots$

假如有一个$01$序列$10010101$，对其进行异或差分得到了$110111111$。

注意末尾多了一位。

有什么用呢？

我们可以发现，当我们要对$[l,r]$进行区间异或时，我们只需要对$l-1,r$这两个点异或就好。

于是现在我们要求的就变成了：

将异或序列每次取反两个间隔一定的点，求序列中所有元素变成$0$的最小次数。

而我们一次在两个$0$上取反没有任何意义。

所以每一次修改要么是把两个$1$变成$0$，要么是一个$0$变$1$，一个$1$变$0$。

如果是后者，我们可以把它看成前面的$1$往后跳了一段。

但是最后还是要和另外一个$1$同时消掉。

于是就变成了点与点之间两两配对求最小代价的问题。

点与点之间匹配的最小代价可以跑$SPFA$搞出来。

当然这个匹配不是二分图匹配。。。

这个匹配时一般图带权匹配。

但是这玩意好像要用带花树啊。。。

蒟蒻表示根本不会。。。

（$PS$：一般图带权匹配可以去$UOJ$找板子。。。我这个菜鸡就算了。。。）

那怎么办？？？

等一下！有效点数好像不超过$16$？

我们可以状压$DP$啊！

复杂度表面上是$O(2^kk^2)$。

但是我们发现我们只要按顺序找到一对没有匹配过的点直接转移就可以了。

所以复杂度实际上是$O(2^kk)$。

仍然可以遍历所有状态。

于是这个题被$\text{差分}+SPFA+\text{状压}DP$完美搞定。

一开始把$m,k$的读入顺序搞反了还$WA$了一发。。。

我的代码里$k$换成了$q$，注意一下。

附代码：

#include<iostream>

#include<algorithm>

#include<cstdio>

#include<queue>

#include<cstring>

#define MAXN 40010

#define MAXM 70

#define MAXK 20

using namespace std;

int n,m,q;

int A[MAXN],B[MAXM],path[MAXN],pos[MAXK],dis[MAXK][MAXK],dp[1<<MAXK];

inline int read(){

	int date=0,w=1;char c=0;

	while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}

	while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}

	return date*w;

}

void spfa(int x){

	int u,s=pos[x];

	queue<int> que;

	for(int i=1;i<=n;i++)path[i]=0;

	path[s]=1;

	que.push(s);

	while(!que.empty()){

		u=que.front();

		que.pop();

		for(int i=1;i<=m;i++){

			if(u+B[i]<=n&&!path[u+B[i]]){

				path[u+B[i]]=path[u]+1;

				que.push(u+B[i]);

			}

			if(u-B[i]>=1&&!path[u-B[i]]){

				path[u-B[i]]=path[u]+1;

				que.push(u-B[i]);

			}

		}

	}

	for(int i=1;i<=q;i++)dis[x][i]=path[pos[i]]-1;

}

void work(){

	int S=(1<<q)-1;

	dp[0]=0;

	for(int i=0;i<S;i++)

	for(int j=1;j<=q;j++){

		if((1<<(j-1))&i)continue;

		for(int k=j+1;k<=q;k++){

			if(((1<<(k-1))&i)||dis[j][k]==-1)continue;

			int x=(i|(1<<(j-1))|(1<<(k-1)));

			dp[x]=min(dp[x],dp[i]+dis[j][k]);

		}

		break;

	}

	printf("%d\n",dp[S]);

}

void init(){

	int x;

	memset(dp,0x3f,sizeof(dp));

	n=read()+1;q=read();m=read();

	for(int i=1;i<=q;i++){

		x=read();

		A[x]^=1;A[x+1]^=1;

	}

	q=0;

	for(int i=1;i<=n;i++)if(A[i])pos[++q]=i;

	for(int i=1;i<=m;i++)B[i]=read();

	for(int i=1;i<=q;i++)spfa(i);

}

int main(){

	init();

	work();

	return 0;

}