【Dual Support Vector Machine】林轩田机器学习技法

这节课内容介绍了SVM的核心。

首先，既然SVM都可以转化为二次规划问题了，为啥还有有Dual啥的呢？原因如下：

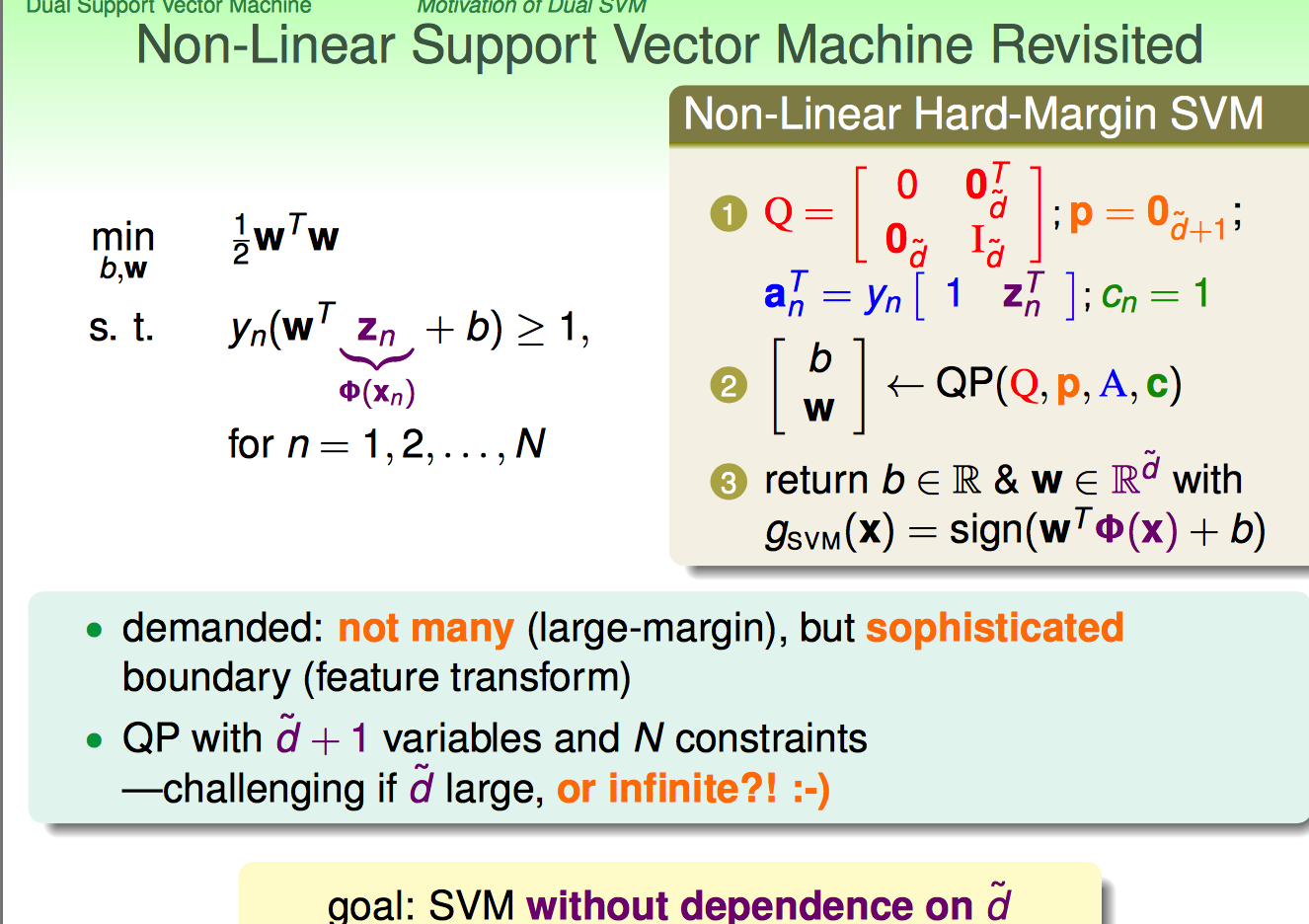
如果x进行non-linear transform后，二次规划算法需要面对的是d`+1维度的N个变量，以及N个约束

如果d`的维度超大，那么二次规划解起来的代价就太大了。因此，SVM的精髓就在于做了如下的问题转化：

不需要问太深奥的数学，知道为啥要dual的motivation就可以了。

这里再次搬出前人的智慧：Lagrange Multipliers

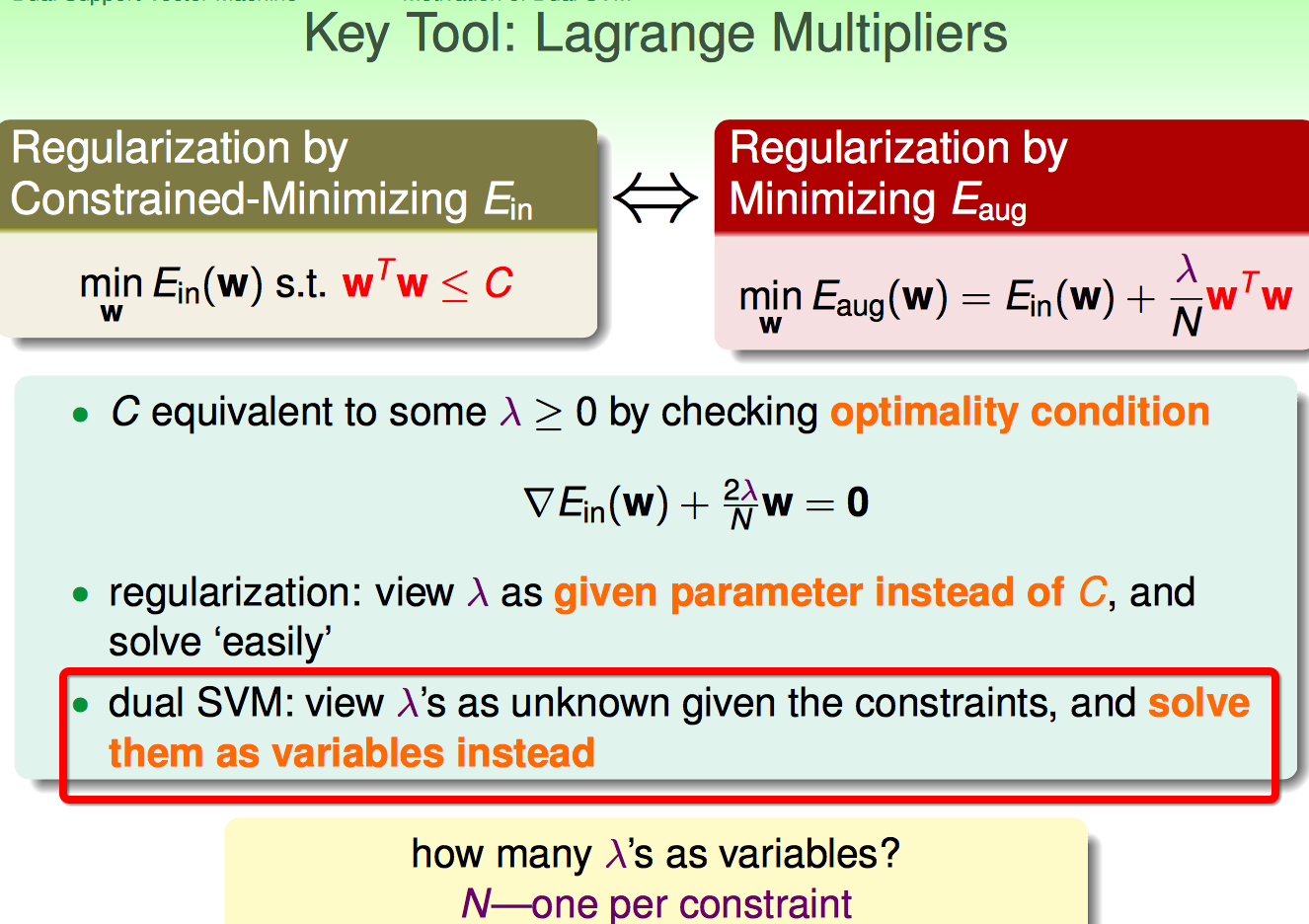
但是这里跟ridge regression不太一样：一个约束条件配一个拉格朗日乘子；每个乘子是未知的，需要求解的变量。

如上图，首先把原问题的N个不等式约束条件，通过拉格朗日乘子给弄到等式中。

问题困惑：原来的目标函数是min (b,W) 0.5W'W，而且还是min；为啥用Lagrange Fucntion转换后，还搞出来一个max呢？背后的原因是啥呢？

我的理解：这里max的目的是把违背约束条件的(b,W)的值无限放大

　　（1）违背约束条件：alpha后面的值是正数，那么max必然是alpha取无限大的情况；这样经过外层的min操作，必然过滤掉了

　　（2）符合约束条件：alpha后面的值是非正，那么max必然是alpha取零的情况；这样min里面剩下的项就是原目标函数了；

综合（1）（2）来看，拉格朗日乘子起到这样的作用：

　　　　a. 把不等式约束给弄到等式中

　　　　b. 把违背约束的项目给弄到无限大

　　　　c. 如果符合约束条件，等式中的拉格朗日项目就没有了；这样剩下的自然就是原来需要min的目标函数

综合b,c来看，拉格朗日乘子用一种特殊的方式把违背约束条件的（b,W)给排除了，把符合约束条件的（b,W)给留在了候选集合中。

这样转换后的问题就跟原问题等价了；约束条件藏在了max里面。

接下需要进一步转化：

交换min和max的顺序：

（1）原来的max里面（b,W)是受到约束条件限制的

（2）交换min和max后，（b,W)可以不受到约束条件限制

转换后的问题，叫Lagrange dual problem。

光大于等于还不行，最好能等于：

要想是强对偶问题，QP需要满足：

（1）原问题是convex的

（2）原问题是feasible的（即线性可分）

（3）约束条件是线性的

于是，就可以放心大胆地取等号了。

分别对b和W求导，获得梯度为零的条件。

通过梯度为0的条件，把min里的b和W都替换掉了；由于min的变量是(b,W)，但现在变量只剩下alpha了，所以min也可以直接去掉了。

这里涉及到一些矩阵微分的内容（http://blog.sciencenet.cn/blog-849193-653656.html）

关于b的梯度求解很直观。

关于W的梯度求解，可以转化成矩阵向量表示。

（1）二次项求导的结果就是W

（2）一次项求导可以做如下的变换，以及最终的表达式如下。

这样W就完全用y,z,alpha表示出来了；另外，从这可以看出来W其实是输入向量Z的线性组合，每个Zn前面的系数就是alphan yn。

以上一系列转化的背后是KKT条件。

有了KKT条件，只要求出来最优的alpha就相当于间接求出来了（b,W).

KKT里面后两个条件比较重要：

（1）dual problem的inner部分要满足梯度为0（即取得最优化的值）

（2）原问题取得最优化值的同时，其中的拉格朗日乘子必须disappear

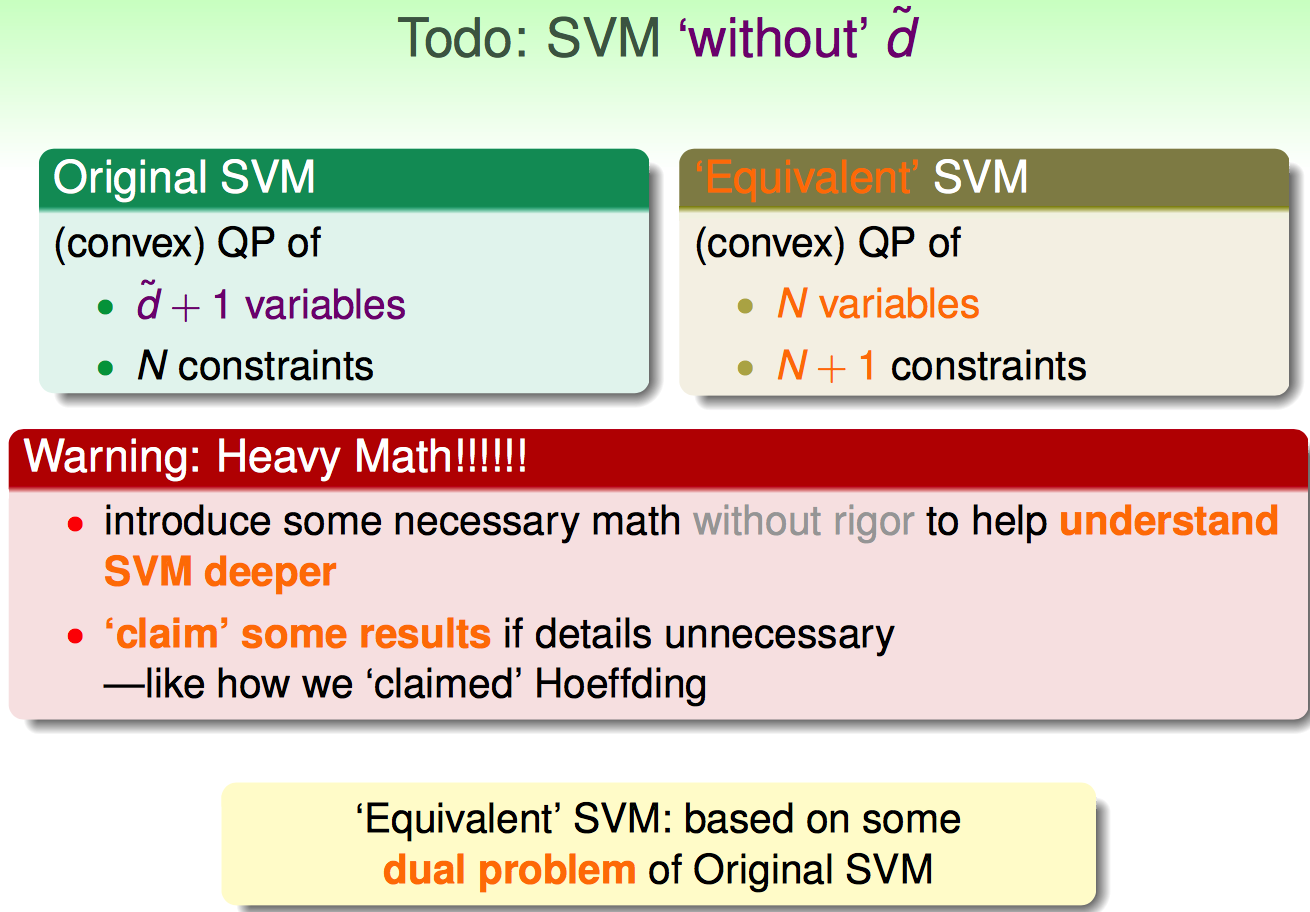
最终，转化为对偶问题后的最优化问题，就保持了N个变量（alpha）,N+1个约束条件。对比原问题，变量的维度控制在了1（原来的维度是d`+1）。

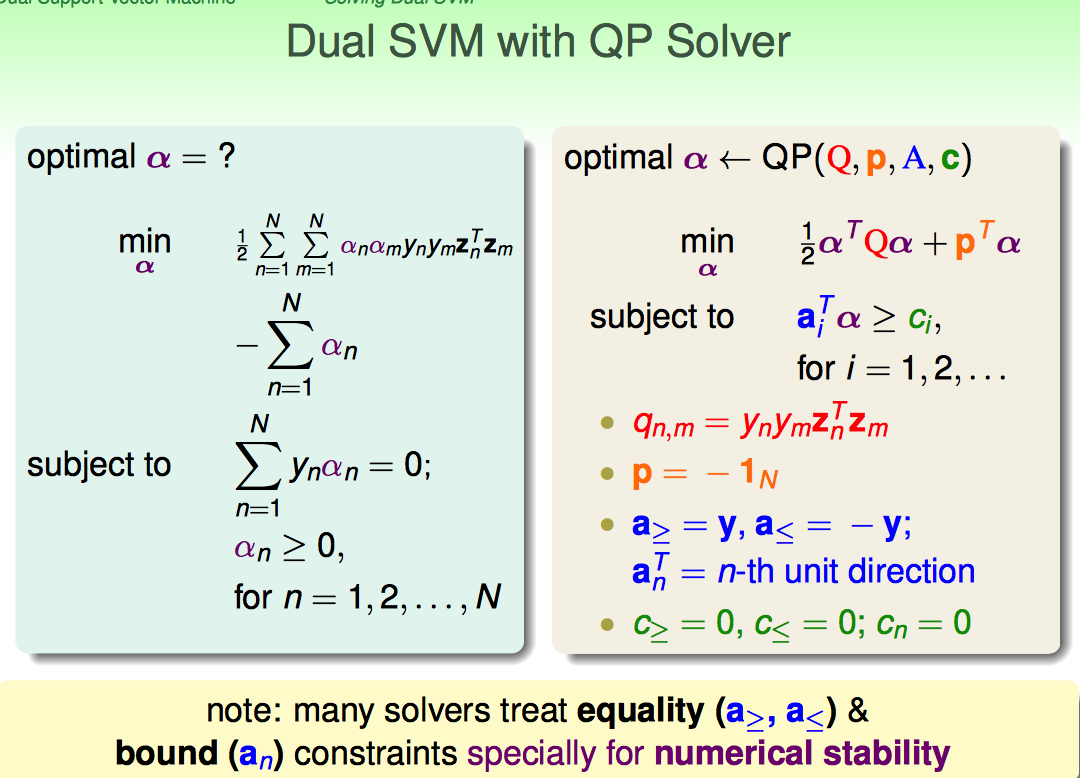
直接套用QP Solver即可

目标函数：

（1）二次项系数qn,m = ynymZn'Zm

（2）一次项系数-IN

约束条件：

（1）等于0的情况可以用“大于等于∩小于等于”来代替

（2）对于alphan大于等0的情况，用n那个单位方向向量做系数（[1,0.....] [0,1,0,....], .... , [0,....,0,1]）

这里提到了一个东西：输入变量d`+1维度的代价哪去了？其实，转化到了qn,m中去了。

其实到这里，还是对为何要转成dual problem不十分确定，只能说是计算的代价发生了变化。

转化后约束条件的系数变得简单了，但是样本维度N一般都会大于输入维度d'很多啊，相当于目标函数复杂了一些。这样计算代价真的降低了么？

估计要想明白这个问题，还得看看QP问题是怎么求解的，后续再看吧。

总之，这里的Q矩阵依然是个N×N的矩阵，如果N很大占用的内存非常多，因此需要把特殊的求解工具才能搞定。

前面一大堆推导，后面的结论就是：

（1）最后只有alpha大于0的点被成为支撑向量（SV）

（2）最终W由所有支撑向量决定

（3）任意一个支撑向量都可以算出来b

这里回顾了之前讲过线性分类模型：W都可以看成输入数据的线性组合；SVM之所以好，是因为W只用支撑向量的线性组合就可以表示了。

这里留了一个问题：如果输入数据经过比较复杂的tranform了，还是比较难搞的，怎么能让算法摆脱d'的限制？