Coursera-AndrewNg(吴恩达)机器学习笔记——第三周编程作业

一. 逻辑回归

　　1.背景：使用逻辑回归预测学生是否会被大学录取。

　　2.首先对数据进行可视化，代码如下：

pos = find(y==); %找到通过学生的序号向量
neg = find(y==); %找到未通过学生的序号向量
plot(X(pos,),X(pos,),'k+','LineWidth',,'MarkerSize',); %使用+绘制通过学生
hold on;
plot(X(neg,),X(neg,),'ko','MarkerFaceColor','y','MarkerSize',); %使用o绘制未通过学生
% Put some labels
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
% Specified in plot order
legend('Admitted', 'Not admitted')
hold off;

　　3.sigmoid函数的实现，代码如下：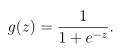

function g = sigmoid(z)  %函数文件名为sigmoid.m
%SIGMOID Compute sigmoid function
%   g = SIGMOID(z) computes the sigmoid of z.
% You need to return the following variables correctly
g = zeros(size(z));
temp=-z;
temp=e.^temp;
temp=temp+;
temp=./temp;
g=temp;
end

　　4.代价函数的实现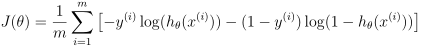代码如下：

function [J, grad] = costFunction(theta, X, y) %函数名文件名为costFunction.m
m = length(y); % number of training examples

% You need to return the following variables correctly
J = /m*(-(y')*log(sigmoid(X*theta))-(1-y)'*log(-sigmoid(X*theta))); %计算代价函数
grad = zeros(size(theta));
grad = /m*X'*(sigmoid(X*theta)-y);  %求梯度
end

　　5.代替梯度下降的优化方法fminunc()，代码如下：

%  参数GradObj设置为on表示，通知函数fminunc()我们的代价函数costFunction()可以返回代价值和梯度值，函数fminunc()可以直接使用梯度值进行计算
options = optimset('GradObj', 'on', 'MaxIter', );
%  Run fminunc to obtain the optimal theta
%  This function will return theta and the cost
[theta, cost] = ...
    fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

　　6.使用计算出的θ_i值做预测，预测函数如下：

function p = predict(theta, X)

m = size(X, ); % Number of training examples
p = zeros(m, );
p=floor(sigmoid(X*theta).*); %因为使用了floor()函数，所以函数值要扩大二倍

二. 正规化逻辑回归

　　1.特征映射(Feature Mapping)：使用两个特征（x₁,x₂）组合出更多的特征如x₁x₂,x₁²,x₂²等。代码如下：

function out = mapFeature(X1, X2)

degree = ;
out = ones(size(X1(:,)));
for i = :degree
    for j = :i
        out(:, end+) = (X1.^(i-j)).*(X2.^j); %一共生成27项
    end  

end
end

　　2.计算在逻辑回归中经过正规化的代价函数和梯度：

function [J, grad] = costFunctionReg(theta, X, y, lambda)

m = length(y); % number of training examples
J = /m*(-(y')*log(sigmoid(X*theta))-(1-y)'*log(-sigmoid(X*theta)))+(/(*m))*lambda*(sum(theta .^) - theta()^); %正规化时不用对θ1正规化
grad = zeros(size(theta)

grad = /m*X'*(sigmoid(X*theta)-y)+lambda*theta/m;
grad() = grad()-lambda*theta()/m;

end