制造业物料清单BOM、智能文档阅读、科学文献影响因子、"Celebrated Italian mathematician ZepartzatT Gozinto" 与高津托图

意大利数学家Z.高津托

意大利伟大数学家Sire Zepartzatt Gozinto的生卒年代是一个谜^[1]，但是他发明的 “高筋图” 在 制造资源管理、物料清单（BOM）管理、智能阅读、科学文献影响因子计算 等方面具有重要应用。

高津托图

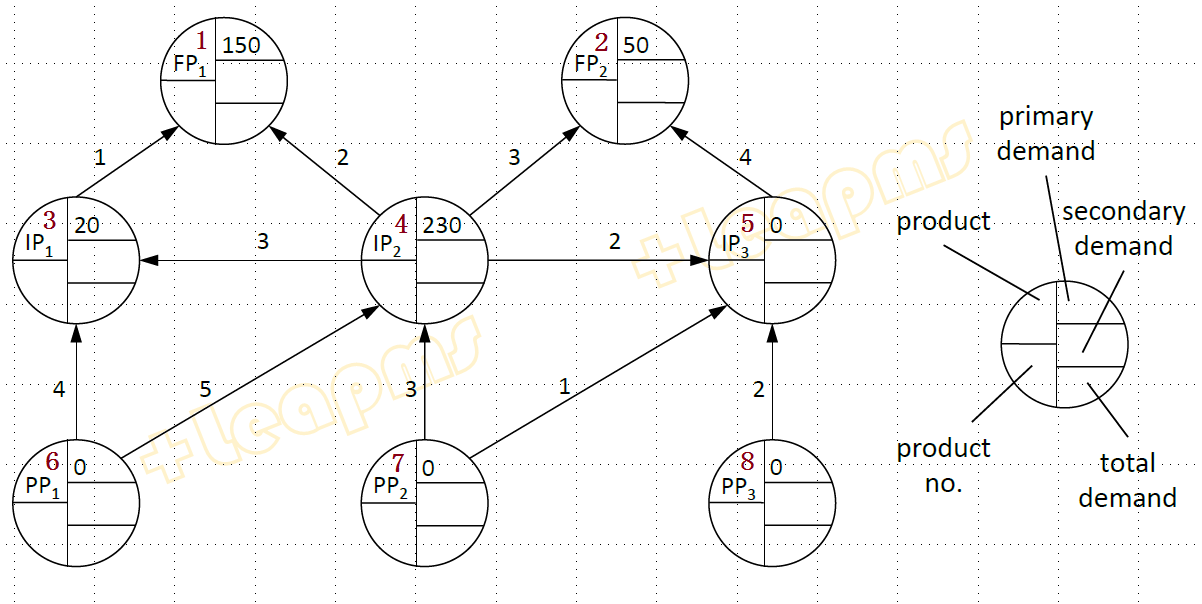
下图是一个制造业物料需求高津托图，节点FP1、FP2分别表示最终产品的需求量，边上的数值表示组装部件所需要的上游零部件的数量，物料清单(BOM)系统需要知道所有零部件的总需求。图中：

Primary Demand（主需求） -- 市场对零部件的需求数量
Secondary Demand（次需求） -- 因产品组装产生的对零部件的需求
Total Demand（总需求）-- 以上两个需求之和
Product No. (产品（拓扑次序）编号）-- 根据组装约束对零部件产品进行拓扑排序的次序数

数学模型

设图中的零部件类型数为n，装配关系（边）数为m

设pd[i]为节点i的主需求(常量）
sd[i]为节点i的次需求（决策变量）
td[i]为节点i的总需求（被动变量）
pd[i]为节点i的产品拓扑次序编号（决策变量）

根据装配逻辑，对任何边k，如果边k的起始节点为a[k]，终止节点为b[k]，权值为c[k]，则：

    sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n

    td[i]=sd[i]+pd[i]|i=1,...,n

把零部件从装配上游到下游排序：

    pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m

    pn[i]>=1|i=1,...,n

    pn[i]<=n|i=1,...,n

+Leapms模型：

min sum{i=1,...,n}pn[i]

subject to

    sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n

    td[i]=sd[i]+pd[i]|i=1,...,n

    pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m

    pn[i]>=1|i=1,...,n

    pn[i]<=n|i=1,...,n

where

    m,n are numbers

    e,pd are sets

    a[k],b[k],c[k] are numbers | k=1,...,m

    sd[i],td[i] are variables of nonnegative numbers|i=1,...,n

    pn[i] is a variable of nonnegative number|i=1,...,n

data_relation

    m=_$(e)/3

    n=_$(pd)

    a[k]=e[3k-2]|k=1,...,m

    b[k]=e[3k-1]|k=1,...,m

    c[k]=e[3k]    |k=1,...,m

data

    pd={150 50 20 230 0 0 0 0}

    e={

        3 1 1

        4 1 2

        4 2 3

        4 3 3

        4 5 2

        5 2 4

        6 3 4

        6 4 5

        7 4 3

        7 5 1

        8 5 2

    }

求解：

+Leapms>load

 Current directory is "ROOT".

 .........

        gozinto.leap

 .........

please input the filename:gozinto

================================================================

1:  min sum{i=1,...,n}pn[i]

2:  subject to

3:

4:      sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n

5:      td[i]=sd[i]+pd[i]|i=1,...,n

6:

7:      pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m

8:      pn[i]>=1|i=1,...,n

9:      pn[i]<=n|i=1,...,n

10:

11:  where

12:      m,n are numbers

13:      e,pd are sets

14:      a[k],b[k],c[k] are numbers | k=1,...,m

15:      sd[i],td[i] are variables of nonnegative numbers|i=1,...,n

16:      pn[i] is a variable of nonnegative number|i=1,...,n

17:

18:  data_relation

19:      m=_$(e)/3

20:      n=_$(pd)

21:      a[k]=e[3k-2]|k=1,...,m

22:      b[k]=e[3k-1]|k=1,...,m

23:      c[k]=e[3k]    |k=1,...,m

24:  data

25:      pd={150 50 20 230 0 0 0 0}

26:      e={

27:          3 1 1

28:          4 1 2

29:          4 2 3

30:          4 3 3

31:          4 5 2

32:          5 2 4

33:          6 3 4

34:          6 4 5

35:          7 4 3

36:          7 5 1

37:          8 5 2

38:      }

================================================================

>>end of the file.

Parsing model:

1D

2R

3V

4O

5C

6S

7End.

..................................

number of variables=24

number of constraints=43

..................................

+Leapms>solve

The LP is solved to optimal.

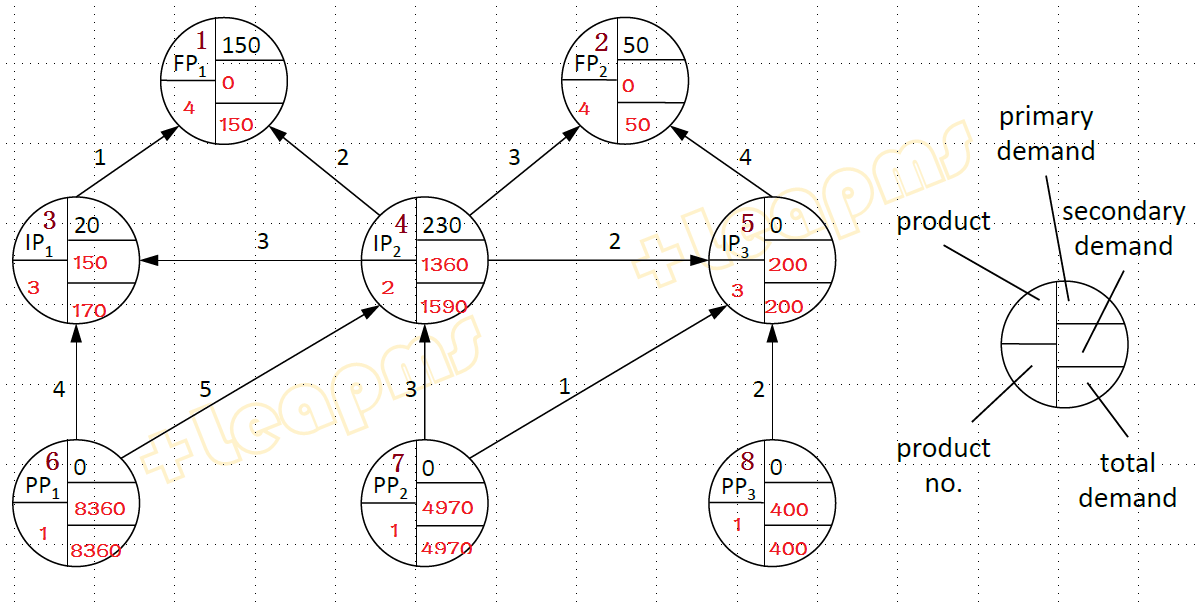
找到线性规划最优解.非零变量值和最优目标值如下：

    .........

    pn1*=4

    pn2*=4

    pn3*=3

    pn4*=2

    pn5*=3

    pn6*=1

    pn7*=1

    pn8*=1

    sd3*=150

    sd4*=1360

    sd5*=200

    sd6*=8630

    sd7*=4970

    sd8*=400

    td1*=150

    td2*=50

    td3*=170

    td4*=1590

    td5*=200

    td6*=8630

    td7*=4970

    td8*=400

    .........

    Objective*=19

    .........

+Leapms>

结果

参考文献

[1] Rousseau, R. . (1987). The gozinto theorem: using citations to determine influences on a scientific publication. Scientometrics, 11(3-4), 217-229.