[八省联考2018] 劈配 mentor

Description

一年一度的综艺节目《中国新代码》又开始了。Zayid 从小就梦想成为一名程序员，他觉得这是一个展示自己的舞台，于是他毫不犹豫地报名了。

Input

轻车熟路的Zayid 顺利地通过了海选，接下来的环节是导师盲选，这一阶段的规则是这样的：

总共n 名参赛选手（编号从1 至n）每人写出一份代码并介绍自己的梦想。接着由所有导师对这些选手进行排名。为了避免后续的麻烦，规定不存在排名并列的情况。

同时，每名选手都将独立地填写一份志愿表，来对总共 m 位导师（编号从 1 至 m）作出评价。志愿表上包含了共m 档志愿。对于每一档志愿，选手被允许填写最多C 位导师，每位导师最多被每位选手填写一次（放弃某些导师也是被允许的）。

在双方的工作都完成后，进行录取工作。每位导师都有自己战队的人数上限，这意味着可能有部分选手的较高志愿、甚至是全部志愿无法得到满足。节目组对”前i 名的录取结果最优“ 作出如下定义：

前1 名的录取结果最优，当且仅当第1 名被其最高非空志愿录取（特别地，如果第1 名没有填写志愿表，那么该选手出局）。
前i 名的录取结果最优，当且仅当在前i - 1 名的录取结果最优的情况下：第i 名被其理论可能的最高志愿录取（特别地，如果第i 名没有填写志愿表、或其所有志愿中的导师战队均已满员，那么该选手出局）。

如果一种方案满足‘‘前n 名的录取结果最优’’，那么我们可以简称这种方案是最优的。

每个人都有一个自己的理想值si，表示第i 位同学希望自己被第si 或更高的志愿录取，如果没有，那么他就会非常沮丧。

现在，所有选手的志愿表和排名都已公示。巧合的是，每位选手的排名都恰好与它们的编号相同。

对于每一位选手，Zayid 都想知道下面两个问题的答案：

在最优的录取方案中，他会被第几志愿录取。
在其他选手相对排名不变的情况下，至少上升多少名才能使得他不沮丧。

作为《中国新代码》的实力派代码手，Zayid 当然轻松地解决了这个问题。不过他还是想请你再算一遍，来检验自己计算的正确性。

Input

每个测试点包含多组测试数据，第一行 2 个用空格隔开的非负整数 T;C，分别表示数据组数、每档志愿最多允许填写的导师数目。

接下来依次描述每组数据，对于每组数据：

第1 行两个用空格隔开的正整数n;m。

n;m 分别表示选手的数量、导师的数量。
第2 行m 个用空格隔开的正整数：其中第i 个整数为$b_i$ 。

$b_i$ 表示编号为i 的导师战队人数的上限。
第3 行至第n + 2 行，每行m 个用空格隔开的非负整数：其中第i + 2 行左起第 j 个数为 $a_{i,j}$ 。

$a_{i,j}$ 表示编号为i 的选手将编号为j 的导师编排在了第$a_{i,j}$志愿。特别地，如果 $a_{i,j}$ = 0，则表示该选手没有将该导师填入志愿表。

在这一部分，保证每行中不存在某一个正数出现超过 C 次（0 可能出现超过C 次），同时保证所有$a_{i,j}$ <= m。
第n + 3 行n 个用空格隔开的正整数，其中第i 个整数为$s_i$ 。

$s_i$ 表示编号为i 的选手的理想值。

在这一部分，保证$s_i$ <= m。

Output

按顺序输出每组数据的答案。对于每组数据，输出2 行：

第1 行输出n 个用空格隔开的正整数，其中第i 个整数的意义为：

在最优的录取方案中，编号为i 的选手会被该档志愿录取。

特别地，如果该选手出局，则这个数为m + 1。
第 2 行输出 n 个用空格隔开的非负整数，其中第 i 个整数的意义为：

使编号为i 的选手不沮丧，最少需要让他上升的排名数。

特别地，如果该选手一定会沮丧，则这个数为i。

Range

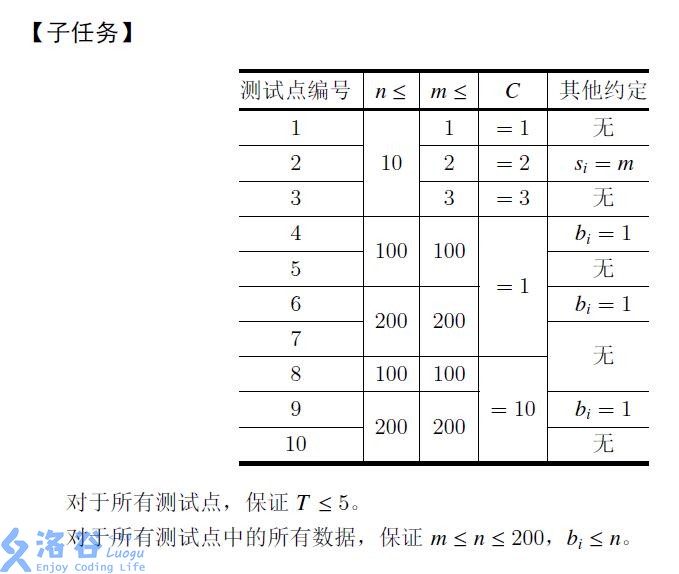
Solution

第一问可以优化，如果第 i 个人的第 j 级志愿不能增广，就直接把这些边删掉。

第二问只需要对于每一个人二分答案 ans[i]，把 ans[i] 之前的人全部按照最优方案建出图，然后额外的连上第 i 个人所期望的边，再寻找增广路，就可以完美解决第二问。

上面的算法可以看出来要很多次建图，又因为图最多只有 2n 的点和 nC 的边，那就可以暴力的存n 个图，分别对应前n 个人的最优方案的残余网络，这样可以大大减少建图浪费的时间，并且每次只需要单路增广。

用 vector 貌似会快一些？

复杂度 $O(不慢)$，第一问最多 nm 次找增广路，第二问 nlogn 次，及时删掉没用的边就不会 TLE 。

以上摘自题解

哇这种直接把一张图保存下来的奇技淫巧学到了啊，很强势

upd：再把 to 写成 flow 就剁手

Code

// By YoungNeal

#include<queue>

#include<vector>

#include<cstdio>

#include<cctype>

#include<cstring>

#include<iostream>

#define N 505

int T,C;

int n,m;

int s,t;

int maxn;

int d[N];

int deg[N];

int ans[N];

int want[N];

int zhiyuan[][][];

struct Edge{

    int to,nxt,flow;

};

struct Graph{

    std::vector<Edge> edge[N];

    void add(int x,int y,int z){

        edge[x].push_back((Edge){y,edge[y].size(),z});

        edge[y].push_back((Edge){x,edge[x].size()-,});

    }

    void del(int x,int y){

        edge[x].pop_back(); edge[y].pop_back();

    }

    bool bfs(){

        std::queue<int> q; q.push(s);

        memset(d,,sizeof d); d[s]=;

        while(q.size()){

            int u=q.front();q.pop();

            for(int i=;i<edge[u].size();i++){

                int to=edge[u][i].to;

                if(d[to]) continue;

                if(!edge[u][i].flow) continue;

                d[to]=d[u]+; q.push(to);

                if(to==t) return ;

            }

        }

        return ;

    }

    int dinic(int now,int flow){

        if(now==t) return flow;

        int rest=flow;

        for(int i=;i<edge[now].size();i++){

            if(!rest) return flow;

            int to=edge[now][i].to;

            if(!edge[now][i].flow) continue;

            if(d[to]!=d[now]+) continue;

            int k=dinic(to,std::min(rest,edge[now][i].flow));

            if(!k) d[to]=;

            rest-=k;

            edge[now][i].flow-=k;

            edge[ edge[now][i].to ][ edge[now][i].nxt ].flow+=k;

        }

        return flow-rest;

    }

    void clear(){

        for(int i=;i<=n+m+;i++)

            edge[i].clear();

    }

}G[N];

void clear(){

    maxn=; s=n+m+; t=s+;

    memset(zhiyuan,,sizeof zhiyuan);

    for(int i=;i<=n;i++) G[i].clear();

}

void read(int &x){

    x=;char ch=getchar();

    while(!isdigit(ch)) ch=getchar();

    while(isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=getchar();

}

bool check(int x,int now){

    int gotonow=now-x;

    if(gotonow<) return ;

    Graph P;

    P=G[gotonow-];

    P.add(s,now,);

    for(int i=;i<=want[now];i++){

        for(int j=;j<=zhiyuan[now][i][];j++)

            P.add(now,zhiyuan[now][i][j]+n,);

    }

    return P.bfs();

}

void write(int x){

    if(x<) putchar('-'),x=-x;

    if(x>) write(x/);

    putchar(x%+'');

}

signed main(){

    read(T);read(C);

    while(T--){

        read(n),read(m);

        clear();

        for(int i=;i<=m;i++) read(deg[i]),G[].add(i+n,t,deg[i]);

        for(int i=;i<=n;i++){

            for(int x,j=;j<=m;j++){

                read(x);

                if(!x) continue;

                maxn=std::max(maxn,x);

                zhiyuan[i][x][++zhiyuan[i][x][]]=j;

            }

        }

        for(int i=;i<=n;i++) read(want[i]);

        for(int i=;i<=n;i++){

            bool o=; G[i]=G[i-];

            G[i].add(s,i,);

            for(int j=;j<=maxn;j++){

                if(!zhiyuan[i][j][]) continue;

                for(int p=;p<=zhiyuan[i][j][];p++)

                    G[i].add(i,zhiyuan[i][j][p]+n,);

                if(G[i].bfs()){

                    G[i].dinic(s,0x3f3f3f3f);

                    o=,ans[i]=j,write(j),putchar(' ');

                }

                if(o) break;

                for(int p=;p<=zhiyuan[i][j][];p++)

                    G[i].del(zhiyuan[i][j][p]+n,i);

            }

            if(!o) ans[i]=m+,write(m+),putchar(' ');

        }

        putchar('\n');

        for(int i=;i<=n;i++){

            if(ans[i]<=want[i]){

                write(),putchar(' ');

                continue;

            }

            int now=-;

            int l=,r=i-;

            while(l<=r){

                int mid=l+r>>;

                if(check(mid,i)) now=mid,r=mid-;

                else l=mid+;

            }

            if(now==-) write(i),putchar(' ');

            else write(now),putchar(' ');

        }

        putchar('\n');

    }

    return ;

}