MT【332】椭圆正交变换

(2018河南数学联赛解答10)

已知方程$17x^2-16xy+4y^2-34x+16y+13=0$表示椭圆,求它的对称中心和对称轴.

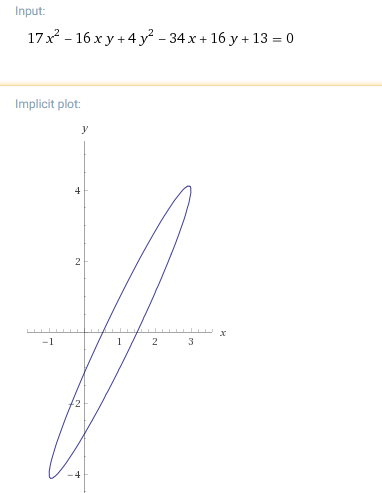
解:设对称中心为$(a,b)$,显然$A(1,1),B(1,-1)$在图像上,
所以对称点$A^{'}(2a-1,2b-1),B^{'}(2a-1,2b+1)$也在椭圆上,
代入作差化简得$b=2a-2,4a^2-8a+4=0$即$a=1,b=0$
作正交变换$(x,y)=(x^{'},y^{'})\cdot(\cos\theta,\sin\theta)$则$\cot2\theta=\dfrac{17-4}{-16}$
记  $k=tan\theta$化简得$8k^2+13k-8=0$即  $k=-\dfrac{13}{16}\pm\dfrac{5\sqrt{17}}{16}$
故对称轴为$y=(-\dfrac{13}{16}\pm\dfrac{5\sqrt{17}}{16})(x-1)$对称中心为$(1,0)$
注:一般的$a_{11}x^2+a_{22}y^2+2a_{12}xy+2b_1x+2b_2y+c=0$
通过正交变换$(x,y)=(x^{'},y^{'})\cdot(\cos\theta,\sin\theta)$后$\cot2\theta=\dfrac{a_{11}-a_{22}}{2a_{12}}$