B-Tree和B+Tree的区别
B+树索引是B+树在数据库中的一种实现,是最常见也是数据库中使用最为频繁的一种索引。B+树中的B代表平衡(balance),而不是二叉(binary),因为B+树是从最早的平衡二叉树演化而来的。在讲B+树之前必须先了解二叉查找树、平衡二叉树(AVLTree)和平衡多路查找树(B-Tree),B+树即由这些树逐步优化而来。
二叉查找树
二叉树具有以下性质:左子树的键值小于根的键值,右子树的键值大于根的键值。
如下图所示就是一棵二叉查找树,
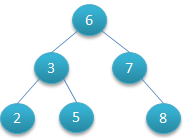
对该二叉树的节点进行查找发现深度为1的节点的查找次数为1,深度为2的查找次数为2,深度为n的节点的查找次数为n,因此其平均查找次数为 (1+2+2+3+3+3) / 6 = 2.3次
二叉查找树可以任意地构造,同样是2,3,5,6,7,8这六个数字,也可以按照下图的方式来构造:
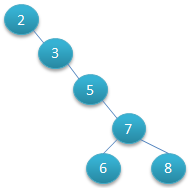
但是这棵二叉树的查询效率就低了。因此若想二叉树的查询效率尽可能高,需要这棵二叉树是平衡的,从而引出新的定义——平衡二叉树,或称AVL树。
平衡二叉树(AVL Tree)
平衡二叉树(AVL树)在符合二叉查找树的条件下,还满足任何节点的两个子树的高度最大差为1。下面的两张图片,左边是AVL树,它的任何节点的两个子树的高度差<=1;右边的不是AVL树,其根节点的左子树高度为3,而右子树高度为1;
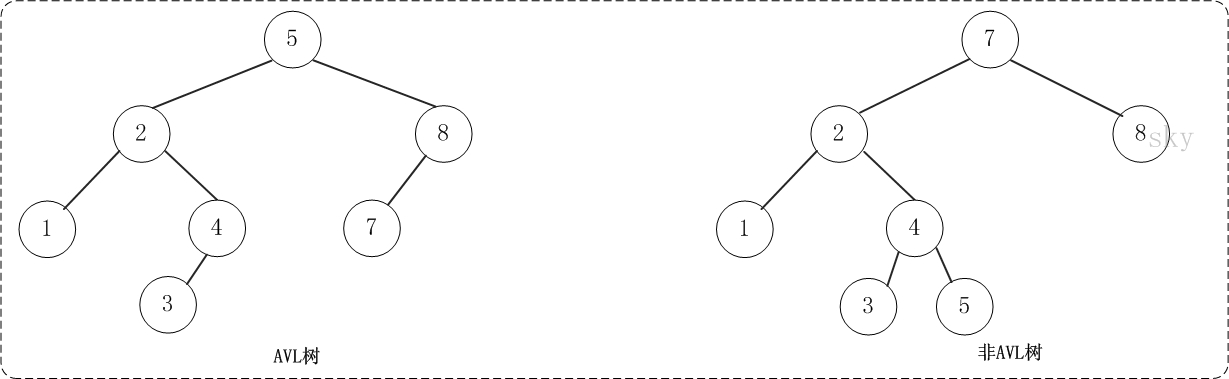
如果在AVL树中进行插入或删除节点,可能导致AVL树失去平衡,这种失去平衡的二叉树可以概括为四种姿态:LL(左左)、RR(右右)、LR(左右)、RL(右左)。它们的示意图如下:

这四种失去平衡的姿态都有各自的定义:
LL:LeftLeft,也称“左左”。插入或删除一个节点后,根节点的左孩子(Left Child)的左孩子(Left Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
RR:RightRight,也称“右右”。插入或删除一个节点后,根节点的右孩子(Right Child)的右孩子(Right Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
LR:LeftRight,也称“左右”。插入或删除一个节点后,根节点的左孩子(Left Child)的右孩子(Right Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
RL:RightLeft,也称“右左”。插入或删除一个节点后,根节点的右孩子(Right Child)的左孩子(Left Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
B-Tree和B+Tree的区别:
在B+Tree中,所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上,而非叶子节点上只存储key值信息,这样可以大大加大每个节点存储的key值数量,降低B+Tree的高度。
B树:

B+树:
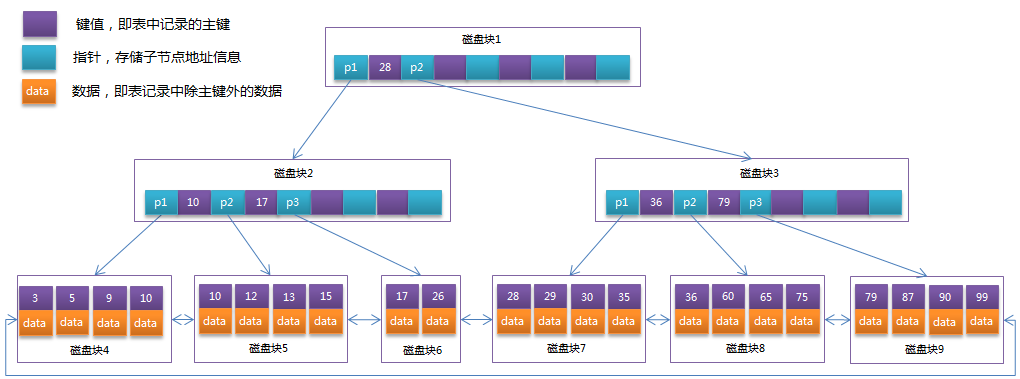
B-Tree和B+Tree的区别的更多相关文章
- WPF中Logical Tree和Visual Tree的区别
The Logical TreeThe logical tree describes the relations between elements of the user interface. The ...
- B-Tree、B+Tree和B*Tree
B-Tree(这儿可不是减号,就是常规意义的BTree) 是一种多路搜索树: 1.定义任意非叶子结点最多只有M个儿子:且M>2: 2.根结点的儿子数为[2, M]: 3.除根结点以外的非叶子结点 ...
- 【Luogu1501】Tree(Link-Cut Tree)
[Luogu1501]Tree(Link-Cut Tree) 题面 洛谷 题解 \(LCT\)版子题 看到了顺手敲一下而已 注意一下,别乘爆了 #include<iostream> #in ...
- 【BZOJ3282】Tree (Link-Cut Tree)
[BZOJ3282]Tree (Link-Cut Tree) 题面 BZOJ权限题呀,良心luogu上有 题解 Link-Cut Tree班子提 最近因为NOIP考炸了 学科也炸了 时间显然没有 以后 ...
- [LeetCode] Encode N-ary Tree to Binary Tree 将N叉树编码为二叉树
Design an algorithm to encode an N-ary tree into a binary tree and decode the binary tree to get the ...
- 平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树
平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树 (a)和(b)都是排序二叉树,但是查找(b)的93节点就需要查找6次,查找(a)的93 ...
- WPF中的Visual Tree和Logical Tree与路由事件
1.Visual Tree和Logical TreeLogical Tree:逻辑树,WPF中用户界面有一个对象树构建而成,这棵树叫做逻辑树,元素的声明分层结构形成了所谓的逻辑树!!Visual Tr ...
- 笔试算法题(39):Trie树(Trie Tree or Prefix Tree)
议题:TRIE树 (Trie Tree or Prefix Tree): 分析: 又称字典树或者前缀树,一种用于快速检索的多叉树结构:英文字母的Trie树为26叉树,数字的Trie树为10叉树:All ...
- LC 431. Encode N-ary Tree to Binary Tree 【lock,hard】
Design an algorithm to encode an N-ary tree into a binary tree and decode the binary tree to get the ...
- 将百分制转换为5分制的算法 Binary Search Tree ordered binary tree sorted binary tree Huffman Tree
1.二叉搜索树:去一个陌生的城市问路到目的地: for each node, all elements in its left subtree are less-or-equal to the nod ...
随机推荐
- SLAM+语音机器人DIY系列:(七)语音交互与自然语言处理——1.语音交互相关技术
摘要 这一章将进入机器人语音交互的学习,让机器人能跟人进行语音对话交流.这是一件很酷的事情,本章将涉及到语音识别.语音合成.自然语言处理方面的知识.本章内容: 1.语音交互相关技术 2.机器人语音交互 ...
- ubuntu:xxx is not in the sudoers file. 问题解决
ubuntu 下普通用户用 sudo 执行命令时报 "xxx is not in the sudoers file.This incident will be reported" ...
- 基于vue-cli快速构建
基于vue-cli快速构建 https://www.jianshu.com/p/2769efeaa10a Vue是近两年来比较火的一个前端框架(渐进式框架吧),与reactjs和angularjs ...
- 【Oracle学习笔记】游标
1. 分类 常见的游标可分为显示游标.隐式游标.静态游标和动态游标四大类: 1.1 显示游标 显式是相对与隐式cursor而言的,就是有一个明确的声明的cursor.显式游标的声明类似如下: delc ...
- C# 切换中英文输入法
在界面输入时,有时需要限定输入法. 在不自定义正则表达式或者其它输入处理的情况下,切换中英文时与当前语言栏匹配,有以下的几种系统方案: InputLanguage方案 使用System.Windows ...
- 简简单单的Vue1(MVVM与Vue的双向绑定原理)
既然选择了远方,便只顾风雨兼程 __ HANS许 系列:零基础搭建前后端分离项目 系列:零基础搭建前后端分离项目 Vue 在此之前的文章我们讲述了前端开发的工具,语言的知识,接下来我们从头开始学习一个 ...
- C# 绘制PDF嵌套表格
嵌套表格,即在一张表格中的特定单元格中再插入一个或者多个表格,使用嵌套表格的优点在于能够让内容的布局更加合理,同时也方便程序套用.下面的示例中,将介绍如何通过C#编程来演示如何插入嵌套表格到PDF文档 ...
- Java学习点滴——Integer缓存
前言 一切从下面这段代码开始 public static void test(String[] agrs){ Integer a = 1; Integer b = 2; System.out.prin ...
- deepin linux 学习笔记(二)——文本编辑器
目录 deepin linux 学习笔记(二)--文本编辑器 前言 nano 小巧的命令行编辑器 通用 编辑 定位 排版 配置 vim 思路独特的超级编辑器 命令模式 插入模式 底线模式(末行模式) ...
- javaFX笔记----ComboBox模仿qq账号下拉框删除账号
myComboBox.setCellFactory( new Callback<ListView<String>, ListCell<String>>() { @O ...
