机器学习基石:07 The VC Dimension

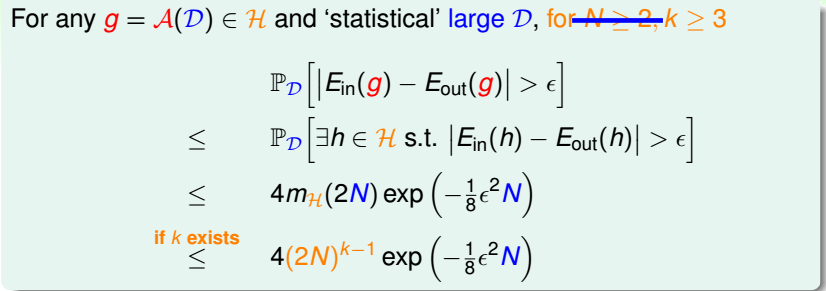












机器学习基石:07 The VC Dimension的更多相关文章
- 机器学习基石笔记:07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- 07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- 机器学习基石7-The VC Dimension
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 前几节课着重介绍了机器能够学习的条件并做了详细的推导和解释.机器能够学习必须满 ...
- 【The VC Dimension】林轩田机器学习基石
首先回顾上节课末尾引出来的VC Bound概念,对于机器学习来说,VC dimension理论到底有啥用. 三点: 1. 如果有Break Point证明是一个好的假设集合 2. 如果N足够大,那么E ...
- 【机器学习基石笔记】七、vc Dimension
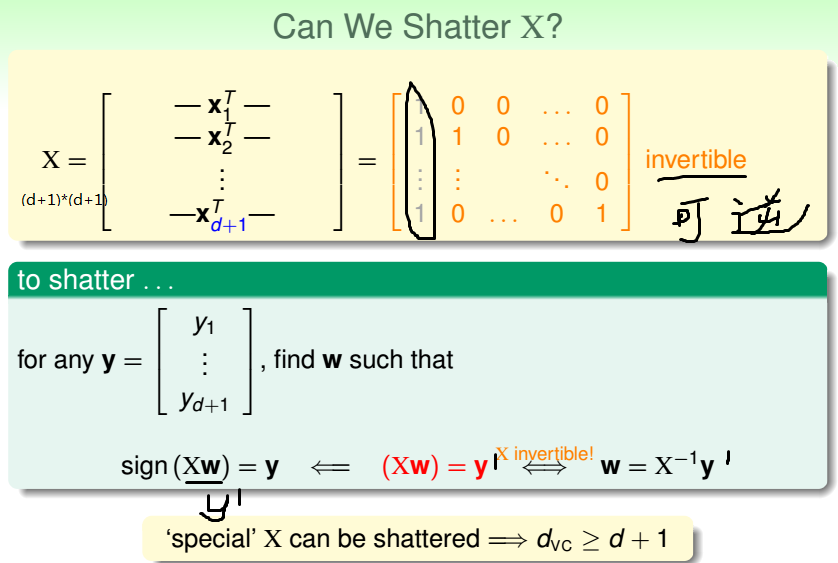
vc demension定义: breakPoint - 1 N > vc dimension, 任意的N个,就不能任意划分 N <= vc dimension,存在N个,可以任意划分 只 ...
- Coursera台大机器学习课程笔记6 -- The VC Dimension
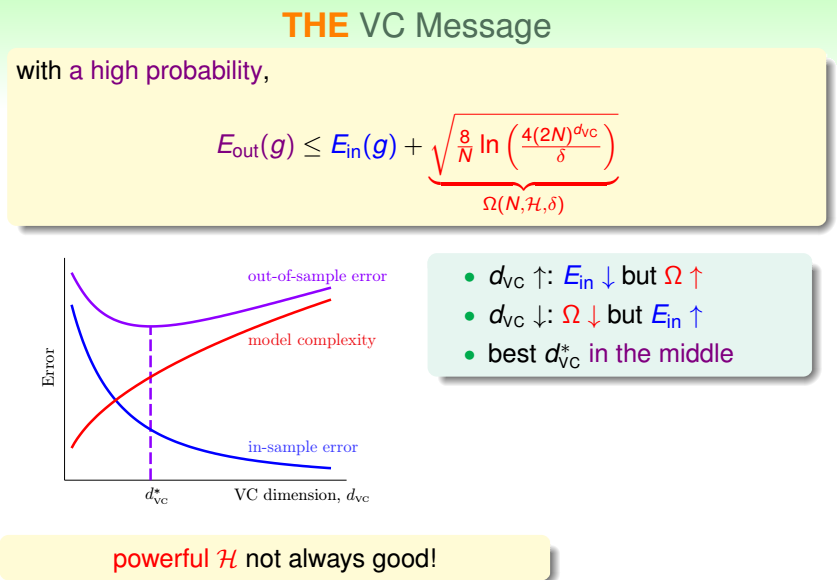
本章的思路在于揭示VC Dimension的意义,简单来说就是假设的自由度,或者假设包含的feature vector的个数(一般情况下),同时进一步说明了Dvc和,Eout,Ein以及Model C ...
- 机器学习基石12-Nonlinear Transformation
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课介绍了分类问题的三种线性模型,可以用来解决binary classif ...
- 机器学习基石8-Noise and Error
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课,我们主要介绍了VC Dimension的概念.如果Hypothese ...
- 机器学习基石11-Linear Models for Classification
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课,我们介绍了Logistic Regression问题,建立cross ...
随机推荐
- (译文)React----React应用程序流式服务端渲染
好处 React16推出了流式服务端渲染,它允许你并行地分发HTML片段.这样可以让渲染 出的首字节有意义的内容给用户速度更快. (例子1,上面部分是一次性转换,下面是流渲染,两种方式) 而且相对re ...
- 《构建之法》教学笔记——Python中的效能分析与几个问题
<构建之法:现代软件工程>中第2章对效能分析进行了介绍,基于的工具是VSTS.由于我教授的学生中只有部分同学选修了C#,若采用书中例子讲解,学生可能理解起来比较困难.不过所有这些学生都学习 ...
- 《团队-手机app便签-开发文档》
项目托管平台地址:https://github.com/Vcandoit/Notepad.git 我主要负责文件存储部分,文字部分使用sqlite保存. 因为我们想实现备忘录记录照片.语音的功能,所以 ...
- 105&250-高级软件工程2017第3次作业
小组成员 2017282110250 王婷婷 2017202110105 张芷祎 github地址 https://github.com/setezzy/Calculator_GUI PSP PSP2 ...
- 201621123054 《Java程序设计》第六周实验总结
1. 本周学习总结 1.1 面向对象学习暂告一段落,请使用思维导图,以封装.继承.多态为核心概念画一张思维导图或相关笔记,对面向对象思想进行一个总结. 1.2 可选:使用常规方法总结其他上课内容. 2 ...
- EasyUI中Tabs添加远程数据的方法。
tabs加载远程数据: $(function () { $("#btnquery").click(function () { if (!$("#tcontent" ...
- C# 使用 GDI+ 画图
最近做一个微信公众号服务,有一些简单的图片处理功能.主要就是用户在页面操作,前端做一些立刻显示的效果,然后提交保存时后端真正修改原图. 我们的后端是 ASP.NET,也就是 C# 语言了,C# 本身处 ...
- 谈谈ASP.NET Core中的ResponseCaching
前言 前面的博客谈的大多数都是针对数据的缓存,今天我们来换换口味.来谈谈在ASP.NET Core中的ResponseCaching,与ResponseCaching关联密切的也就是常说的HTTP缓存 ...
- Mego(08) - 高级建模
对于模型建立Mego还提供了一些高级主题 数据库函数映射 我们可以将现有的CLR方法映射到指定数据库的标题函数上,如下所示 public class OrderManageEntities : DbC ...
- URL编码和Base64编码 (转)
我们经常会遇到所谓的URL编码(也叫百分号编码)和Base64编码. 先说一下Bsae64编码.BASE64编码是一种常用的将二进制数据转换为64个可打印字符的编码,常用于在通常处理文本数据 ...
