3D数学矩阵常用知识点整理

1.矩阵了解

1）矩阵的维度和记法

　　　　(先数多少行，再数多少列)

2)矩阵的转置

　　　　　　　　行变成列，第一行变成第一列...矩阵的转置的转置就是原矩阵

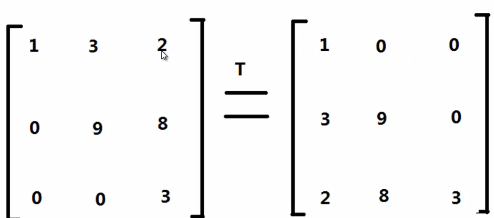　　　　　　　　即

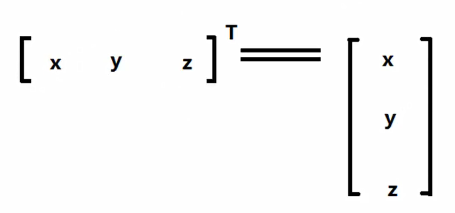
3)矩阵和标量的乘法

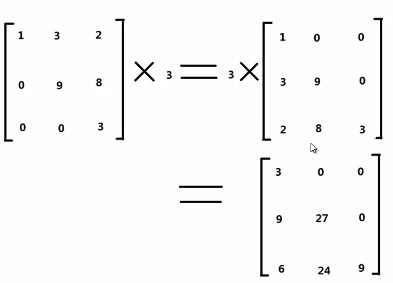
4)矩阵和矩阵的乘法

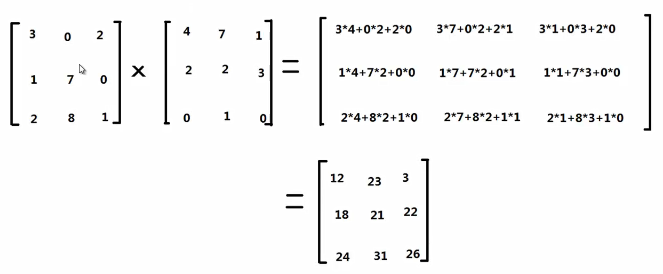
　　　　例.[2,3]X[3,4] =[2,4]

　　　　矩阵的乘法不支持交换律,强调顺序，左乘和右乘是不一样的。

　　　　NXM阶与SXT阶矩阵相乘，必须满足M和S维度相同，乘法的结果是一个NXT矩阵。

5)单位矩阵

　　　　　　主对角线全部为1，非主对角线都为0，则为单位矩阵。

　　　　　　单位矩阵乘任何矩阵，任何矩阵都不变。

2.矩阵变换

1）2D变换

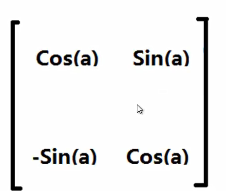
　　　　　　①绕坐标中心旋转a角度

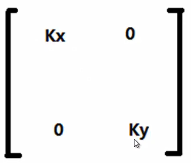
　　　　　　②缩放矩阵

　　　　　　　　　　沿坐标轴缩放

　　　　　　　　　　(k分别为x轴，y轴上缩放因子)

　　　　　　　　　　沿任意N轴缩放

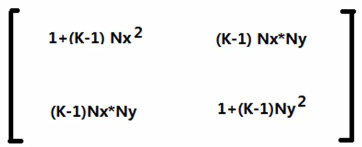
2）3D变换

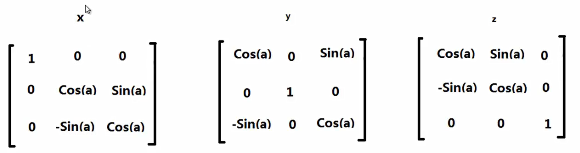
　　　　　　①绕x，y，z轴旋转a度

　　　　　　②缩放矩阵

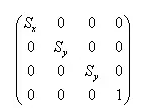
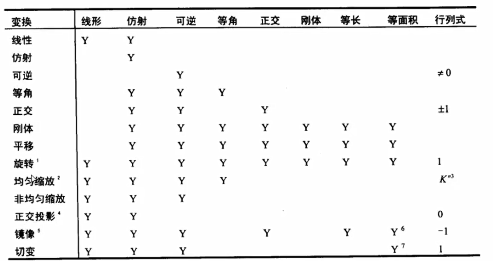
3）变换的种类

　　　　　　旋转缩放平移镜像

　　　　　　切边（正方形上面拉一下，变成平行四边形，称之为切边）

　　　　　　投影（分为平行投影：Unity中正交相机，对物体大小不产生变化；透视投影：近大远小效果）

　　　　　　可逆（施加了一个变换，还可以撤销）

　　　　　　总结分类：

　　　　　　　　　　线性变换

　　　　　　　　　　仿射变换：线性变换+平移。

　　　　　　　　　　所有的线性变换都是仿射变换，但并不是所有的仿射变换是线性变换。

4）常见变换组合

　　　　　　　　　　满足结合律 a*b*c = a*(b*c)

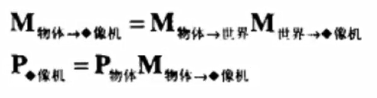
总结：一般可以使用矩阵转换工具进行变换。物体只需要乘一次工具矩阵即可完成变换。　　　　　　

3.变换深入

　　　当我们使用2x2旋转过后，我们只需要旋转后的xy分量各自加上也可。但是没有一个统一的工具去解决。为了能够

把平移和其他的线性变换都组合在一起，利用矩阵这一工具去实现。我们需要把这个矩阵做一个扩展，在2d中平移需要扩展

为3x3的矩阵。

1）2D平移（3X3矩阵）

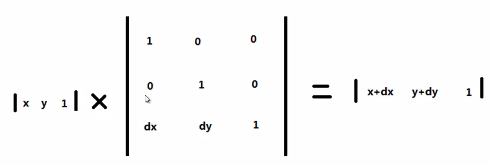
　　最后一个分量为何不取0？

　　第一次做了平移之后如果为0，又要做平移，参与第二次分量计算，因为其分量为0，都为0了。所以没有达到平移的目的。

2）3D平移（4X4矩阵）

3)3D 旋转+平移

4)透视投影(近大远小)

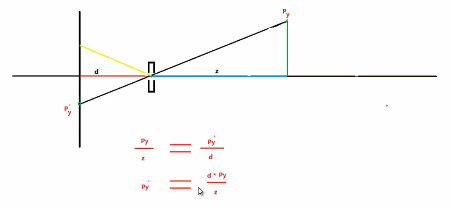
　　注意：这边本可以比较简单的使用等角三角形原理进行计算，但是还是使用矩阵来进行计算，因为可以方便的和其他

矩阵进行组合计算。

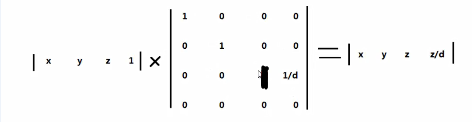
　　注意：这边的最后一个坐标分量的值不是1.

4.方阵

　　定义：行数和列数相等。

1）二阶方阵行列式

2）三阶方阵行列式

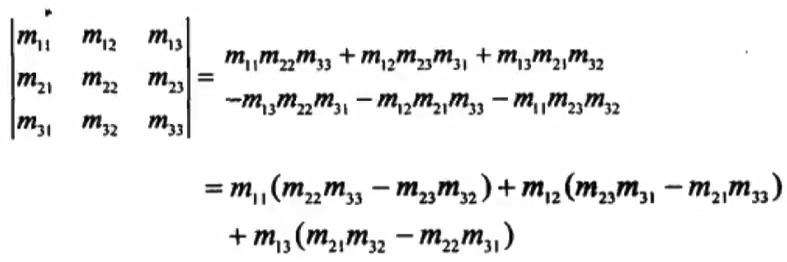
3)4阶行列式计算　

　　　　　　代数余子式

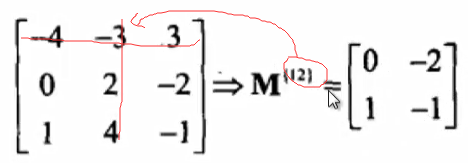
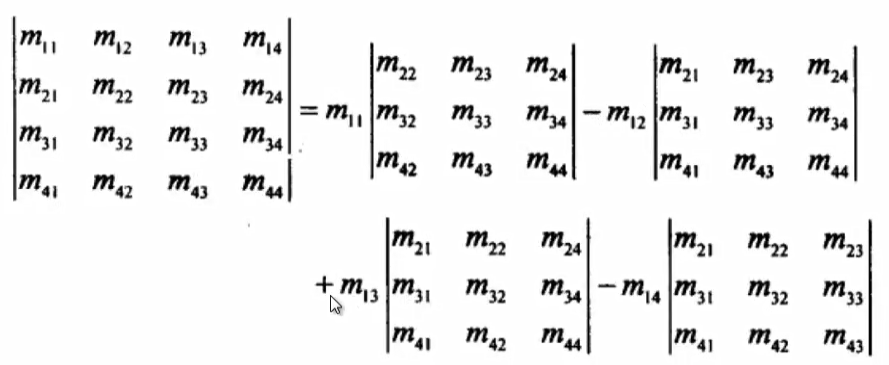
　　　　从方阵中任选一行中数，用这一行中每个元素去乘每个代数余子式。

　　　　注意计算方式，正负值取决于行列下标（1开始的）

　　　　行列式性质：

　　　　　　　　矩阵积的行列式等于矩阵行列式的积：|AB| =|A||B|

　　　　　　　　矩阵转置的行列式等于原矩阵的行列式：|M的转置| =|M|

　　　　　　　　如果矩阵的任意行或列全为0，那么他的行列式等于0

　　　　　　　　 “把矩阵的任意两行或两列进行交换”，行列式变负

　　　　　　　　任意行或列的非零积加到另一行或列上不会改变行列式的值

4）矩阵的逆

　　　　　　①逆的定义

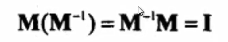
　　　　　　对于一个矩阵是否有逆，如果一个方阵他的行列式为0，成为奇异矩阵，没有逆。

有逆，则他的行列式一定不为0.

　　　　　　代数余子式矩阵（对矩阵中每一个元素都取代数余子式）

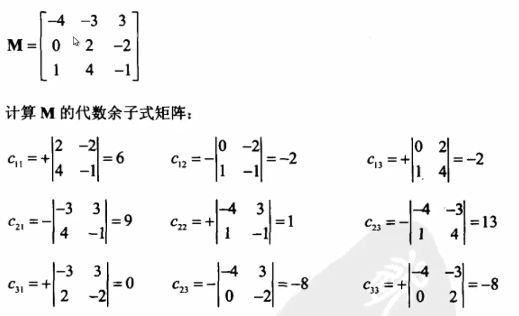
　　　　　　标准伴随矩阵

　　　　　　　当我们得到代数余子式矩阵之后，需要把这个代数余子式矩阵进行转置，称为标准伴随矩阵。

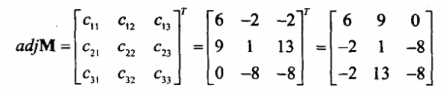
　　　　　　矩阵求逆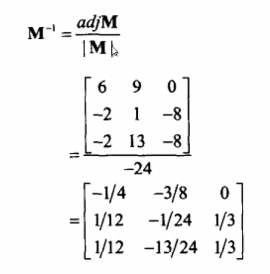

　　　　　　定义检测

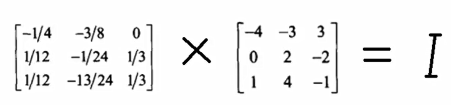
（主对角线都为1，其他都为0）

　　　　　　②矩阵逆性质

　　　　　　③正交矩阵和逆

　　　　　　　　若方阵M是正交的，则当且仅当M与它的转置的乘积等于单位矩阵。

　　　　　　　　M*M的转置 = I（单位矩阵）,即如果发现他是正交的，则可以把他的转置当做逆来使用。

　　　　　　　　应用：

　　　　　　　　　　仅仅拥有旋转，仅仅包含镜像。都是正交的。如果要撤销一个旋转，不用去求他的逆，直接用他的

转置就可以代替逆来使用。　　　　