关于回文串的DP问题

问题1：插入/删除字符使得原字符串变成一个回文串且代价最小

poj 3280 Cheapest Palindrome

题意：给出一个由m中字母组成的长度为n的串，给出m种字母添加和删除花费的代价，求让给出的串变成回文串的代价。

Sol:

• 插入和删除等价，因此只需要保留 min（插入代价，删除代价）作为调整字符串的代价
• 如果 s[i]==s[j]，那么将区间（i，j）变为回文串的代价和将区间（i+1,j-1）变为回文串的代价相同，因为此时不需要修改
• 如果不同，必然要将 s[i]和s[j]改为同一字符
• 第一种情况是，想要将（i，j）变为回文串，可以是在（i+1，j）已是回文串的基础上，在j后面添加字符 s[i]，或者直接将i处的字符 s[i] 删掉，取代价小的操作即可
• 另一种情况是，如果（i，j-1）是回文串，可以将j处的字符删掉或在i前面填加字符s[j]，同样取代价小的方式操作

Code:提供几种不同的写法，加深理解

 #include <stdio.h>
 #include <string.h>
 #define mem(a) memset(a,0,sizeof(a))
 #define MIN(a,b) ((a) < (b) ? (a) : (b))

 int DP[][],cost[],N,M;
 char str[];

 int main()
 {
     while(~scanf("%d%d", &M, &N))
     {
         mem(DP); mem(str); mem(cost);
         scanf("%s%*c",str);
         char ch; int x, y;
         for(int i=;i<M;i++)
         {
             scanf("%c %d %d%*c", &ch, &x, &y);
             cost[ch-'a'] = MIN(x,y);
         }
         for(int i=;i<N;i++)
         {
             for(int j=i-;j>=;j--)
             {
                 DP[j][i] = MIN(DP[j+][i]+cost[str[j]-'a'], DP[j][i-]+cost[str[i]-'a']);
                 if(str[i] == str[j])DP[j][i] = MIN(DP[j][i],DP[j+][i-]);
             }
         }
         printf("%d\n", DP[][N-]);
     }
     return ;
 }

1

     #include<iostream>
     #include<algorithm>
     using namespace std;
     typedef pair<int, int> P;
     #define ad first
     #define de second
     int n, m, dp[][];
     char s[];
     P ch[];           //ch[ch-'a'].ad代表add一个ch的代价，ch[ch-'a'].de代表delete一个ch的代价
     int main()
     {
         cin >> n >> m >> s;
         for (int i = ; i <= n; i++)
         {
             char Ch;
             cin >> Ch;
             cin >> ch[Ch - 'a'].ad >> ch[Ch - 'a'].de;
         }
         for (int i = ; i <= m; i++)
             dp[i][i] = ;
         for (int i = ; i < m; i++)             //注意for循环要实现从短串到长串的过渡，这里i代表长度为i+1
             for (int j = ; j + i < m; j++)
                 if (s[j] == s[j + i]) dp[j][j + i] = dp[j + ][j + i - ];
                 else
                 {
                     int aa = dp[j + ][j + i] + min(ch[s[j] - 'a'].ad, ch[s[j] - 'a'].de);
                     int bb = dp[j][j + i - ] + min(ch[s[j + i] - 'a'].ad, ch[s[j + i] - 'a'].de);
                     dp[j][j + i] = min(aa, bb);
                 }
         printf("%d\n", dp[][m - ]);
         return ;
     }  

2

     #include <cstdio>
     #include <string>
     #include <iostream>
     #include <algorithm>
     #include <cstring>
     using namespace std;
     const int N = ;
     const int M = ;
     int add[N];
     int dp[M][M];  

     int main()
     {
         int n,m;
         string s;
         while(~scanf("%d%d",&n,&m))
         {
             cin>>s;
             char c;int x,y;
             for(int i=;i<n;i++)
             {
                 cin>>c>>x>>y;
                 add[c]=min(x,y);
             }
             memset(dp,,sizeof(dp));
             for(int k=;k<s.size();k++)
             {
                 for(int i=,j=k;j<s.size();i++,j++)
                 {
                     dp[i][j]=0x3f3f3f3f;
                     if(s[i]==s[j])
                         dp[i][j]=dp[i+][j-];
                     else
                     {
                         dp[i][j]=min(dp[i+][j] + add[s[i]],dp[i][j]);
                         dp[i][j]=min(dp[i][j-] + add[s[j]],dp[i][j]);
                     }
                 }
             }
             printf("%d\n",dp[][s.size()-]);
         }
         return ;
     }  

3

---

问题2：插入最少多少个字符使得原字符串变成一个回文串

poj 1159 Palindrome

Sol:

首先第一种方法是：

这道题相当于是上一个题中的修改代价为1的情况

因此列出方程：

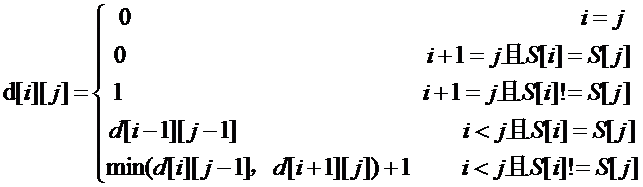
从上面的分析可以看出，这个问题的实质是求最长公共子序列，只是这两个序列分别是串S的前一部分和串S后一部分的逆序列。

由此引出第二种方法

第二种方法：

先说结论：设原序列S的逆序列为S'，最少需要补充的字母数 = 原序列S的长度－S和S'的最长公共子串长度

最后这道题需要对内存进行优化

Code:

 #include <iostream>
 #include <cstdio>
 #include <cstring>

 using namespace std;

 #define MIN(a, b) ((a) < (b) ? (a) : (b))

 #define MAXSIZE 5005

 //开始没有考虑内存问题，使用了int型，超内存限制，也可使用滚动数组解决
 unsigned short d[MAXSIZE][MAXSIZE];

 int ToPalindrome(char *s, int n)
 {
     int i, j, k;
     //只有一个字符时，不需要添加字符
     for (i = ; i < n; i++)
     {
         d[i][i] = ;
     }
     //串长度为2时
     for (i = ; i < n; i++)
     {
         if (s[i-] == s[i])
         {
             d[i-][i] = ;
         }
         else
         {
             d[i-][i] = ;
         }
     }

     //串长度递增
     for (k = ; k < n; k++)
     {
         for (i = , j = k; j < n; i++, j++)
         {
             if (s[i] == s[j])
             {
                 d[i][j] = d[i+][j-];
             }
             else
             {
                 d[i][j] = MIN(d[i][j-], d[i+][j]) + ;
             }
         }
     }
     return d[][n-];
 }

 int main(void)
 {
     char str[MAXSIZE];

     int n;
     while (scanf("%d", &n) != EOF)
     {
         getchar();
         gets(str);
         printf("%d\n", ToPalindrome(str, n));
     }
     return ;
 }

1

 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<iostream>
 using namespace std;

 const int N=;
 int n;
 char a[N],b[N];
 int f[][N];

 int main(){
     while(scanf("%d",&n)!=EOF){
         scanf("%s",a+);
         for(int i=;i<=n;++i)
             b[i]=a[n-i+];
         memset(f,,sizeof(f));
         for(int i=;i<=n;++i)
             for(int j=;j<=n;++j)
                 if(a[i]==b[j]) f[i%][j]=f[(i-)%][j-]+;
                 else f[i%][j]=max(f[(i-)%][j],f[i%][j-]);
         printf("%d\n",n-f[n%][n]);
     }
     return ;
 }

2