[luogu P3384] 【模板】树链剖分 [树链剖分]

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1： 格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2： 格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3： 格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4： 格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例#1：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

输出样例#1：

2
21

说明

时空限制：1s，128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=100000，M<=100000

（其实，纯随机生成的树LCA+暴力是能过的，可是，你觉得可能是纯随机的么233）

样例说明：

树的结构如下：

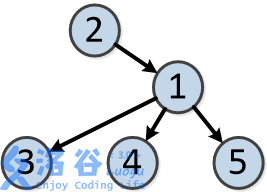
各个操作如下：

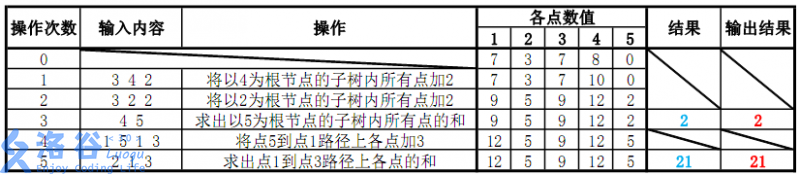
故输出应依次为2、21(重要的事情说三遍：记得取模)

---

My Solution

哪来的什么solution

因为这题快颓了week了

统计：2/29   AC!!!

为什么我之前要用树状数组嘞

向unsigned大佬低头    orz

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 using namespace std;

 typedef long long ll;

 inline int read(){
     char ch;
     int re=;
     bool flag=;
     while((ch=getchar())!='-'&&(ch<''||ch>''));
     ch=='-'?flag=:re=ch-'';
     while((ch=getchar())>=''&&ch<='')  re=re*+ch-'';
     return flag?-re:re;
 }

 inline ll rea(){
     char ch;
     ll re=;
     bool flag=;
     while((ch=getchar())!='-'&&(ch<''||ch>''));
     ch=='-'?flag=:re=ch-'';
     while((ch=getchar())>=''&&ch<='')  re=re*+ch-'';
     return flag?-re:re;
 }

 struct edge{
     int to,next;
     edge(int to=,int next=):
         to(to),next(next){}
 };

 struct Segment_Tree{
     int l,r;
     ll sum,tag;
 };

 const int maxn=;

 int cnt,n,m,root;
 ll mod;
 edge edges[maxn<<];
 Segment_Tree tre[maxn<<];
 int head[maxn],top[maxn],dep[maxn],fat[maxn],id[maxn],id_[maxn],son[maxn],siz[maxn];
 int data[maxn];

 inline void add_edge(int from,int to){
     edges[++cnt]=edge(to,head[from]);  head[from]=cnt;
     edges[++cnt]=edge(from,head[to]);  head[to]=cnt;
 }

 void init(){
     n=read();  m=read();  root=read();  mod=rea();
     for(int i=;i<=n;i++)
         data[i]=read();
     int from,to;
     cnt=;
     for(int i=;i<n;i++){
         from=read();  to=read();
         add_edge(from,to);
     }
 }

 void dfs_1(int x,int fa){
     fat[x]=fa;
     siz[x]=;
     dep[x]=dep[fa]+;
     for(int ee=head[x];ee;ee=edges[ee].next)
         if(edges[ee].to!=fa){
             dfs_1(edges[ee].to,x);
             siz[x]+=siz[edges[ee].to];
             if(!son[x]||siz[edges[ee].to]>siz[son[x]])
                 son[x]=edges[ee].to;
         }
 }

 void dfs_2(int x,int fa){
     if(!son[x])  return;
     top[son[x]]=top[x];
     id[son[x]]=++cnt;
     id_[cnt]=son[x];
     dfs_2(son[x],x);
     for(int ee=head[x];ee;ee=edges[ee].next)
         if(edges[ee].to!=fa&&edges[ee].to!=son[x]){
             top[edges[ee].to]=edges[ee].to;
             id[edges[ee].to]=++cnt;
             id_[cnt]=edges[ee].to;
             dfs_2(edges[ee].to,x);
         }
 }

 inline void push_up(int x){
     tre[x].sum=tre[x<<].sum+tre[x<<|].sum;
 }

 inline void push_down(int x){
     tre[x<<].tag+=tre[x].tag;
     tre[x<<].sum+=tre[x].tag*(tre[x<<].r-tre[x<<].l+);
     tre[x<<|].tag+=tre[x].tag;
     tre[x<<|].sum+=tre[x].tag*(tre[x<<|].r-tre[x<<|].l+);
     tre[x].tag=;
     return;
 }

 void build(int x,int l,int r){
     tre[x].l=l;  tre[x].r=r;
     if(l==r){
         tre[x].sum=data[id_[l]];
         return;
     }
     int mid=(l+r)>>;
     build(x<<,l,mid);
     build(x<<|,mid+,r);
     push_up(x);
 }

 void make(){
     dfs_1(root,);
     cnt=;
     top[root]=root;
     id[root]=cnt;
     id_[cnt]=root;
     dfs_2(root,);
     build(,,n);
 }

 void update(int x,int L,int R,ll c){
     if(L<=tre[x].l&&tre[x].r<=R){
         tre[x].tag+=c;
         tre[x].sum+=c*(tre[x].r-tre[x].l+);
         return;
     }
     push_down(x);
     int mid=(tre[x].l+tre[x].r)>>;
     if(R<=mid)  update(x<<,L,R,c);
     else  if(L>mid)  update(x<<|,L,R,c);
     else{
         update(x<<,L,mid,c);
         update(x<<|,mid+,R,c);
     }
     push_up(x);
 }

 ll query_sum(int x,int L,int R){
     if(L<=tre[x].l&&tre[x].r<=R)
         return tre[x].sum;
     push_down(x);
     int mid=(tre[x].l+tre[x].r)>>;
     if(R<=mid)  return query_sum(x<<,L,R);
     else  if(L>mid)  return query_sum(x<<|,L,R);
     else  return  query_sum(x<<,L,mid)+query_sum(x<<|,mid+,R);
 }

 void change(int u,int v,ll c){
     int f1=top[u];
     int f2=top[v];
     while(f1!=f2){
         // this ensure u and v is not at the same heavy chain
         if(dep[f1] < dep[f2]){
             // ensure that heavy chain 1 is under heavy chain 2
             swap(f1,f2);
             swap(u,v);
         }
         update(,id[f1],id[u],c);
         u=fat[f1];
         f1=top[u];
     }
     if(dep[u]>dep[v]) swap(u, v);
     update(,id[u],id[v],c);
 }

 ll find_sum(int u, int v)
 {
     ll sum=;
     int f1=top[u];
     int f2=top[v];
     while(f1!=f2)
     {
         if(dep[f1]<dep[f2])
         {
             swap(f1,f2);
             swap(u,v);
         }
         sum+=query_sum(,id[f1],id[u]);
         sum%=mod;
         u=fat[f1];
         f1=top[u];
     }
     if(dep[u]>dep[v])  swap(u, v);
     sum+=query_sum(,id[u],id[v]);
     return sum%mod;
 }

 void solve(){
     int opt,ss,tt;
     ll c;
     for(int i=;i<m;i++){
         opt=read();
         if(opt&){
             //opt==3
             if(opt&){
                 ss=read();  c=rea();
                 update(,id[ss],id[ss]+siz[ss]-,c);
             }
             //opt==1
             else{
                 ss=read();  tt=read();  c=rea();
                 change(ss,tt,c);
             }
         }
         else{
             //opt==4
             if(opt&){
                 ss=read();
                 printf("%lld\n",query_sum(,id[ss],id[ss]+siz[ss]-)%mod);
             }
             //opt==2
             else{
                 ss=read();  tt=read();
                 printf("%lld\n",find_sum(ss,tt));
             }
         }
     }
 }

 int main(){
     //freopen("data.in","r",stdin);
     init();
     make();
     solve();
     return ;
 }

---

爱你锋利的伤痕  爱你成熟的天真