CTR预估中的贝叶斯平滑方法（二）参数估计和代码实现

1. 前言

前面博客介绍了CTR预估中的贝叶斯平滑方法的原理http://www.cnblogs.com/bentuwuying/p/6389222.html。

这篇博客主要是介绍如何对贝叶斯平滑的参数进行估计，以及具体的代码实现。

首先，我们回顾一下前文中介绍的似然函数，也就是我们需要进行最大化的目标函数：

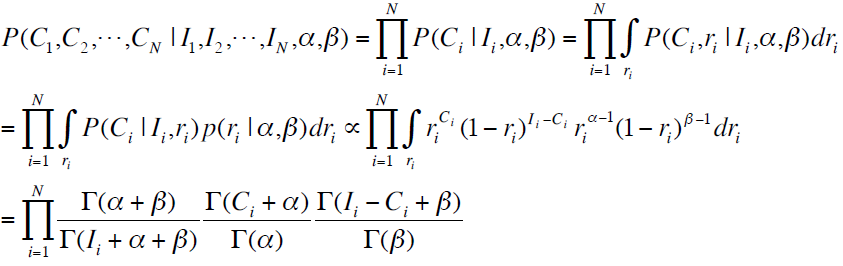
下面我们就基于这个目标函数介绍怎样估计参数。

2. 参数估计的几种方法

1. 矩估计

矩估计在这里有点乱入的意思：），因为它其实不是用来最大化似然函数的，而是直接进行参数的近似估计。

矩估计的方法要追溯到19世纪的Karl Pearson，是基于一种简单的 “替换” 思想建立起来的一种估计方法。其基本思想是用样本矩估计总体矩. 由大数定理，如果未知参数和总体的某个(些)矩有关系，我们可以很自然地来构造未知参数的估计。具体计算步骤如下：

1）根据给出的概率密度函数，计算总体的原点矩（如果只有一个参数只要计算一阶原点矩，如果有两个参数要计算一阶和二阶）。由于有参数这里得到的都是带有参数的式子。比如，有两个参数时，需要先计算出：期望aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCABDAPgDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD9U6KKKACiiigAooooAKKKKACiiigAooooAKKKy9f8UaN4Uto7jW9XsdHt5ZBEkt/cpAjueiguQCT6UAalFIrBlDKQQRkEd6zbbxHp134iv9CiuN+q2Ftb3lzb7GGyKZpVibcRtO4wSjAJI28gZGQDTopGYIpZiFUDJJOABWZ4f8UaN4stHutE1ex1m1jkMTz6fcpOiuOqlkJAIyOKANSiiigAooooAKKKKACiiigAooooAKKKKACiiigAoor51/bv+Mnin9n34A6t4/8ACmsWNjqOmy28MdhqFiLiO9aWeOPbnepUqpduM/dPFJuw0rn0VRXhng3w18b9f8DaJqWp/EjRdI1y906C4ubMeExLHazvGGeP/j6UsFYkdicdq1f2a9U+J+p+HPE6/FS40m71ix1+6sLG40a0a2gntIgipLtZmOWfzO/GAOcZqrWbRN7pM9eoryLS/inffFT4n674X8G3KWugeE7lLXxB4gEaymS9wHOn2wbK7kUqZpGB2bwiruJaP12l5jCiivHtG+K+o+CPi1p/w08dTRzz63BLc+GPEaRiJdUEQBmtZ0GFS6jUh8oAkiklVQgpR1sHmew0UUUAFFFFABX5yfGL9mm0/wCChv7QPxg07UvHGqeG3+HVxp2i6JDDAlzaRCWAy3MkkBKlneUEBldTiNc7sAD9G6+DP2F/ERuf21/2u9PLZEmt28qj08ma6jP/AKEPypJXlZ9n+n6XG3aN/NH1z4B+GM3w5+DWheA9J8Q3vn6PpMWmW+tzxpLODGgUS7HBU9OFOQBgc4ryfQfhn8QD8cvGaj4rarFINB0Yte/2HYfvh5+pYjwYto2cnjn95z0FfSVFU3d3YlorI+Qvit8A/Efji9vtC0rwCmn6tq2ozvrvxH/tG3ibUdIaV3awDo5uiZYilv5ckXkwglkLbEr2H4Y6Xp83jX+0NA8B3fgTSrHS30u6S6sIrEXUgkiMKJHGSJFhVJgJPufv8RswL49copLQHqFFFFABRVLWtZsfDuj32randR2Wm2MEl1c3MxwkMSKWd2PYBQSfpXzX4U1z4oftQfBzUvH3hLxQ3w9l1eVn8G2UtujxRWscwVbq+BRmkkmVZGEYPlqroCrnLUAfUNFY2reILTwX4Ruta8S6lbWllplm11qOoOPLhRY03SSYydq8E4yfTmuN+DHjDxD8U9Ig8c30TaF4a1aDzdE0GSJftDWrEGO6unOSJJFAZYkwEWTDF2+4Ael0UVkeKrDVtR0S4i0PVE0fVRh7e6mt1uItwOQskZILIejBWVsE7WU80Aa9FeafBX4zRfFKHX9J1GxGheN/C95/Z3iDQ/N8z7NMV3RyxsQC8EyYeNyBlSQQCpA9LoAKK81/aP8AElx4K+B/jPxNbeI77wtNoml3Oopf6fFbSyFo4mZI9txFKhDNtGNuScAEVz37GWreNfEv7NXgjxD8QtYm1zxXrtodWubqWGOHEc7tJAqpGqqoETR8ADnNC1v5A9LHtdFFFABXwf8A8FG7y/8AiZ8V/gH8FdGsU1q41bXG8Rajpjz+Qs1taKcIz4barJ9p5IIBQHBr7k1bV7DQNOn1DU72306wt13zXV3KsUUY6ZZmIAH1NfnL8Kv2hPhl8R/+CjvxI+I2v+P/AA5pXh3wvoUXh7w3d6tqkFtDdEsPOlgeRgrgN9owVJyswPQ0LWSXz+7/AIIPSLfy+8+obD4nfFTxF+0X4V8Fax4Jt/B3huHTLrxBealbawL77eI8W6WoxGnlhZLiOQ5yW2ADADZ9L+O3j6T4V/BXx34whCm50PRLy/gVhkNLHCzRg/Vgo/GvFPi1+3X8I/CdzbWvgjxBonxE+JmstFo+iaboVyt2ss8zhYllniJSOIO6lvm3HHAJHHrXx3+H2ofEf9nbxx4OWf7brGq+Hbqxjn2hPOuWgYI20cDMmDjpzUyvyO3n/X5FRtzq/wDX9ankn/BMrRDpv7G/g3UZ5GuNT16e+1e/uZDl55pbuUb2PdtiICT6V5/+2jrXxS/Zu8c+E/ilpnjfxNqvwdGqRReK/D8BhaSwjeTAkify93lNnbtJyGCruxINvoH/AATH15Na/Ys8BQYKXWlm9066hYYaKSO7m+Vh2O1kOPervxH+InhP9pP4q33wB07xFp9xplnb/avGUdveKJ7mIPgaZDtO7czLmd15jQbMhpMppP4/d+Xp/lYiPw+98/X/AIc1Pgt/wkfxe+IesfFGHxhr1v8ADC6ZYvDPh9yiQ6gijEl+4aPzFikbPlR7hlV3nh1A83/4KrNeeH/2dtD8c6RL9l17wb4q07WLG6X70bhnjxn0JkUkd9orzr9lb486N+yT8dPFf7MvjTxlYXfhaxuWn8Ja/dXse21WQ7zp9y+cRyAscBsfOGHR0Fejf8FX5Zr/APZZg8M2MJu9Y8T+JNN0nT7ZOXmnaRpFVR7+Vj8aiW0XHy/MqO7UvP8AI+tvCXiGHxd4U0XXbddtvqdlDexqTnCyRq4H5NXnfxX+J/xM8GeJILHwd8GL34h6W9qsz6rbeIrDT1jlLODD5dw4ckBVbcBg78dQa7/wP4cXwd4K8P6Ar+Yulafb2IcfxCKNUz/47XAfFf4YfEzxn4kgvvB3xnvfh5paWqwvpVt4dsNQWSUM5M3mXCFwSGVdoOBsz1JqpW5tNiY7anF/8L8+PH/Rruq/+Fto/wD8dr1L4R+NfGfjXSr648afDq5+HN5DMI4LO51e11E3CbQTIGt2YLg8YPPFeW/8KD+PH/R0Wq/+ETo//wAar1L4R+CvGfgrSr638afEW5+I15NMJILy50i10426bQDGFt1UNk85PPNAHeV+aP8AwT+1CSX/AIKHftSxNwJNQ1FiP9zVGUfo1fpdX5sfsC6f5H/BQz9qeQj7moXwz/v6k7f0pR/iL0Y5fB80fpPRRRQAUUUUAcn8S/DfibxT4XnsfCfi+TwTrDBvK1SLT4L0odpC5jmBUjJBPfjFfIn7P/xi+NX7SPwO1HwRpfiC28LfE/wze3ui+JvGd7pwnWGaGQrCkMPyo00o4Z+RGI2bbudBXvHjX9q/wxoHxS1T4U6Rb32s/FGK0hnsdGFpIsFy0oypacKVSOMEPI54Vc7dzDbXzn8ENcm/Za/bJ+MXgHWpr7xBe+N7Kw8UaMIoCJNV1BlZLsRqoKxh53lOWISNIsswVSaSV3bv+f8AVwei9Py/qxT/AOChehfEfQP2UvB+g6t8Tb/UPE2uT6d4Vu9N0y0t4LbXL6RmZ5Xfy/OClUIKoyq2BleSK+y/gh8M7z4P/DjSfCV14mu/FMWlxJbWlzd2lvbGG3SNUjhVII0XaoXgsCxycsa+b/2h7aT4wft6fAT4fovm6d4QtLnxzqqL8yqysI7Un3E0Sj6SV9mVS2b7v+vxuJ7pdl/X4WPiT/gqr4uuk+FPgT4eWk72y+PPFNppd4yHBa1Vgzr+MhhP0BHevsm+0OK50F9JtZ59Kg8kQRS6ewjkgUDA8s4IGABjiviv/gq94cuIPhz8NPiHDE81t4K8XWl5fBRny7eRgC59vMSJf+BivtXVvEWlaBoVzrep6la6fo9tAbme/uZljgiiAyXZycBcc5JpL4X6/oinuvT9WfAmkfGz4g/st/tLeLvAHxf8UeKfHej+INMaTwBdW0cSvfTFtq2oEcaj7SzMkYYkKrKCQFkBH11+zz8P/GfgTwLbj4geNNR8Y+K71VmvWunjNvZscnyIAiLlVztLtkuVz8oIUfMHxH8G6H/wUL+F3in4h2XjO20XTvDjzx+B7qK+EC6ZPbuGkv705BiaZolCq+DFCEfAZzj0T9gr9tPSP2nPhzaaZrep2Vt8TdJT7Nqmnecive7B/wAfcCg/OjAZbbwrZHClSSO1uv6f1v8A8OS979P1/r+tjivH3iOb4V/8FWfAf2R/K034heEW07Uox92SaFrh4pCO7DyYUB7Bm9a9y+Kvx01KL4r6J8IPh/DbXvjvUrY6lqOoXaGS08P6aDtNzMgIMkjEhY4sjLEFiFxu8J+K2gS/Ef8A4KsfCi2s0Mtt4M8JzaxqUi9It7XMcak9iXkhOPRq539nX4x+HPhV+2F+05D8S72bTPG+sa5ANGtZLSWa51DTo/NW2jtURWaQmMw/Ioy3y4B2nBHVJPz/AD/z/AqWjbXl+RY/4KJaT4si0r4cfCrSfHOq6sfijrEWh6laamkDM0aTwSG5i8uNPK2nAcL8hVzlcgGvQP2w/FPxD/Zf0Twh8RPC3i5l+G2gavYWOs+Dv7LtzGNObbDlZ9plyvAAzjLqf4cHx3WvFV5rf/BSTTPE/j+1voIPBfg6bW7Tw7bxC4bTkkLIAwU7WkWGRriVwSAy+WhcpGX9a+KPjWx/4KAfs8eKNJ+Gx1CXwnNo1xc3N/cWj273OoxoXtNPjDj5isyJJK6EqAsaAt5jbVe0eZd7/d/wz+8LJyt8vv8A+HR6LpekfGb4i/FPwn4+sfGtl4Y+GAeVn8FyaYGur2zaMiGeaZvmEshKv5eE8pdoO5t4orO/YT+PVv8AGf4CeA4raG5vL7S9EisdavXjZI7e7g2wiIswG+SQI0pC52rtLY3pkq2uXREJ3V2fSlFFFSUFFFFAHiPhf4Yaj8C/id4i1XwrYtqPgLxjff2jqujW5Am0nUmAWS8gUkCSGUBTLGPnVlDIGDMq+3UUUdLB5hXig+Gl/wDF34u+H/Hvi6wfTdA8JiV/DGgXODM91IoV9QuVBIVgg2xRcsgZnba52J7XRR1uHkFFFFABRRRQAV8Hfsb+HX0j9v8A/avYoQBc2cmSP+e7PMPzHNer/t4ftH/EL9mf4e6D4h8AeC4PFrXOpC31GW6gmnitIdpIysLKwLn5Q5O0EYIJYCov2LtJ1vxfq3xK+NniLwhc+BdR+I13p72+hXzl54bWzs0gSRyVUjzHMzAFR8u09waI/E5dk/xsEvh5e9vwPp+ivP8AxTrXxTtNduYvDfg3wfq2jLt8i71XxbdWNxJ8oLboU0yZVw24DEjZAB4JwOH8e+LvF1np+nt8Qr6L4W6GzztPqvgzUn1XLqIzDHLPPp8fkK2ZjxGdxiRfMG/Y4B7xRXxh4T8U3/iHSvEPjTx78QfEPhrxVIzDwRoc19Jpb3FlGoS0uG0tWWO7nupAWeN43wZFRUjwBX2XbtI9vE0yCOUqC6A5CtjkZoAaLSAXRufJj+0lBGZto3lM5C564yScV518S/iXqHw/8eeC7WLwHqviHR9YF5DqPiLS7aW5bR1jjEkatDDFJI4lcBR91QVyT0Fel0UAeL/BP4UXunfEHx78VPE9p9k8VeMJoYILF2V20vS7dAlvbllJHmPgyybSV3uFBOwMfaKKKPIDC8c+CdG+JHg7WPC/iKyTUdE1a1e0u7aTo8bDBweoI6gjkEAjkVxfwO0bxV8PNEt/APiXzdattFtxDpPihSpF9ZphYkuFzmO5RSqtxtkC71OS6J6jRQAVleJtZuNB0ae7tNKu9bu1wsNhZbRJM5OANzlUQerMQAPyOrRQB5R8E/g3P4F1bxX4z8ST2+ofEHxhcpc6vdWuTBbRRrst7K3LAExQpxuIBdizkDIVfT20+1e9W8a2hN4iGNbgxjzAuc7Q3XHtViigCIW0K3LXAiQTsoRpQo3FQSQCeuASePc0lraQWNukFtDHbwIMJFEoVVHsBwKmooAitrWGziEVvDHBECW2RqFGSSScD1JJ+poqWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIZbO3nngnlgjkmgJMUjoC0ZIwdp7ZHHFTUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH//Z" alt="" width="124" height="33" /> ; 方差 aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXMAAAA7CAIAAAAGpP1wAAATtElEQVR4nO2dX0wcR57Hf0/9Mn4YlNFohAlOhj2P7SCCMBKsBh+zPs5mD1sY4RZkIbfGPux4WTbYIZ4kGGGEuYAObk3OXEK848MIc6YPVqBbYwswmkUHWRxAZtZBySggMRJIw0M/dKTOwzz0PdRM0/One7pnuqdxtj5PMFPdXV39m29X/X6/qgIOg8Fg1Ab0rgAGg/kJgpUFg8GoD1YWDAajPlhZMBiM+mBlwWAw6oOVBYPBqA9WFgwGoz5YWTAYjPpgZdEWqs/p7KP0rgUGk2qwsiTC8vxUfQ1JkuTd0WnpkjKVZW1x6gJJkiTZOzylUh0xGD3ByqKYPicJAiqv9UoUjqksMyP9VosRAMrrPmEC3OqMywBQWf8RRVE3G2vLaloCWtYfg0kBWFmU4X74KURi2fxRtHy0suyuz54jG3w0y3Hc3PhAy7/9x4ks46lLrXyB4a7fPnR/r9kdYDCpACuLItiTWcYIXSHMOXR4H2O4t5UMUZhrs+UW8v9+2PnlUHfbS8EB/S21AIaFLWbveOa7tu6hVN0RBqMJWFkUsPtiEgDea/+vAONvd141EmAwZbgmFiKKrS3OUSGu1ZWX113j/52eXw5TlgBzIsuYUVgZdjxWFsyrD1YWBYz13QCA+8+88g+JNRpyn6ms89Esx9IfX64gjJbR//nvh09W+QJP77Xi0RDmVQcriwJuVBUBwMDUN/IPienBXZ0Zyc+2AkCGLXdiYZ3jONfvW5zt3RRFtTvrz2EP7n6C8W923rxGkuSFq9cW1xS8VP7GwcqigKqiNwGge2he/iHy81kmXT0kSXbeHcWysn9g/Os5FmNxaQVJnjEAABj6owa/mJhgZVGA4zABANd7R+Qfsjg1PDy1qF2VMJry7y3vzaxuor/93ueZRsKQnkdj7ZcBVhb5/JhvAQCoaenXuyaYFDH7bFb4753magBY3tGrOq8SWFnkQ791AACgpO6W3jXB6MNI73VIO5Z8nwVFD+cW19SoVKpgaYqi/IzcmweO43zeNSoey+ubidVn/S9T71T8hlZ41Mb8xKXGmyidbN+wYwUAgPyzjXrXJEhibas189MTcc2JZ355XfpsGtlPYgbWdrGkuvkzhXUJY2X6kb3IfrOzl6JGjpgJR9UN6V8q4990Xv2XPy1uKLwOXX/2V3PJ+5vpDZIkM0yGYO6W4fCubFXd67OszY3vnQIACGOFIN0LfZZhy61vdMr2kLM979eWVDXI1zkhHvdYdnbOg8dLCRyrCT94XwMAgNcLK/SuCpdk22rK3GNqoLfTYiSQzQgTBREoLoZo6nkkfiZt7UepgbG764cP2bxJvO2GuhsNJutzr5/jOGbr/wwAAMSLXdHyCxOu/IK/d3sSeakz/s0KR379R3dUeDkHmII3DgBAQWWT/IPCRkM9TZXoeZPOvohyLO3r7bzJm0t53QdxnjdL15QWlNbdSsbwfR53himtpX9/zBWmvzmAJPewQ+eaqNG2WnOrrgSZyrA7xvvWuzKdk2ECgEmxH1ZK7EeRgTX/c9nYQpwelgQzrtsAcGc8KGQBxt9YX+PscYmVp/pb0q0FXj8jViA+LE2WHC8orUm26x+gj6UBALQNPJF/UJiyUH1OMWVB0D5vyfGMYP/leIl4Z5K9XFqQmVeW/AvVMztIANx2zSR7ouTZWQ6+Z1/L/UHPeqjWtprScOY4AIDh0LaIjXie3iPMx0V+N6mzH5kGNtbX2j2UuBHS3iWTAbJOVMu8oRnXbSCMs57thK+ICDDbeZnGgtLLyWjL1sIjNBZaEnuWsVCmLBzHsbTPkWNBxXIctTEvNdB2EYAYX9qSXw8JWi+dAsL4ZDVBR49a/OB9FurCv+7T71etbttqBltwkACAnLIrokV2lsV61ym2n7gFFib6P+2fSKYOTecLAKBjcDZ+UY7bXH1iJCBJhw6P5+k9ALjYNpDwGQbaLgKAOadMkdUrVhaO47Y9T3l/TOu9pxHfbq1MGgCOnLqkpBpSsNsrRgJMtpP6vqXpb6ZCN33gG528pqq3rUbQL5/EdaMEdr8dnvpL9Oeptx/pAs+n7rf+Pmwa1+P/nVRUga2lcQIACPO3cqJKAeakzQSE2bOrWvii9mQWgGFyJUGlriw4CADVzXcUHZWIsnAc11x9IugtPlQQ/jwC1Sey5MuzTK6U5QBA82fjKp5TKTvLFO93/EqfTosmbasFj3qaUEM9ealUg/WxH7ECbqovzWgRup+L87Ob7yiyQ7babovTfRMw/lmz/MIymR3sAFAwFhMSoF+mAQDA4Oy3ig5MUFm+nR3kf2bCS37vfggAAGkvo+TZu7YYHXREbuDFucfCD6O9N5P9LQCgb/rj5vwQf8tTenRaNGpbLbhYcgwAiIMFEVcLMFv3JBfN08t+YhZgd9dryGhqvpdthQHG39oQXCdMllYG6Lx0Q0xfKUv7om8f5YJEZI2seX2RZ919gQYZ8ma6BlDaADq5e7gLICrezNLT88sxa+j1BX8aCSoLx24dDIaJoOrGXuHmajsApB0riW5779pid7tTENcmPu4eCFnGZIHVBACmDFv3XVe0Zex8PYaO4V3rqcf77D5fdUqPNEyN2lZ9QrZRcrEt4pt7rZf6J19IHKqX/ahvYMx3aRCDln6pkdTS+B1ULLqvx9K+EdfdXFsGfypHxWVeWZpqSgEAwFDvbI9WFo4LFL1JAIC9ulni6izta3dedRT/k2uEokZc9mxrxeXb12sdAHC8vIHjuPXl+asXQkkD4Q7m1ZkRlLPCq3OiysJxJSgjFeDt0suhqm0fMgAAFFXdEDtqfWEsFLkWLncUqD6RZTlaJBpjCz0n6abRlGWqj3+oihZSUAft2lZtXkz2o0p0DbuFn0+6OgyEeUOiFjraj9oGFmD8qAdRV24HAMJ8ZISiKIralHwKSFiBeHNHpFcUYPx8/KSpZ5T/fPyzZiCM96eei535cunbAFKhuqXHD6wWY0PXA/4TlvYeCuk46kOtL89TFNV5sxE9grxzDaik4KEAn6GTuLLUOA6jwpb8s+iTDfcw+qTulpQjevxOMyqWV3YFNeDsYAdhzFzdlBhiBEVXPE4ZZHFqOEYHVoq6HfG1JoV8NdLLN56ihRRUQcu2VZmuhnJUh+JSPteSRJlQh+zVEgfqaj9yDUwptY7DIDfHjDluJgDgwFslEoVQABsACGOmZ5vhOI7Z9mQaCelkk74bVajRYqYXUf0tBMDl25HJNWQRymkkFrbCBOnpvVYAQINWlvbm/CxrzO2hfV5nYz2foZO4srz3y1xU+LXcX6JP0MJIANASJ0THXizJQyU7Bmdp75LFeKB/Mk4vtKLwdXSTX4vpefgtyOY1r7zslGf3O/lj+qjIQabWaNq2qhJwHDYAgPmIfW/oP+KyZ1sB4ErHoMSR+tqPTANTRmhgKD0IQgR2vkYv/sOOGumSTwbaBNrK1jpyHLUt0oeM9F5Hh9zoG4v4CqXw8TItpPTtNIgZbw7dV9ewu/XSmQHBumU8iStL6EnsZbt3N55Fn/SOfCV9LFJZADCYbEV5mUJPjRiNZ/PRyYfm9UlsEfZZUq8smratijAbbvTziAhSsrseMwHjS1KpX/rajxYG9vLJADqnnBgZHyIorLger2zgSllQW0+fPmXJccSdADE/1I3Kn23sDrvo6hMjAWBIR92fMELyETPejJz01mPHftXUE/OKCStLsPcIglGxkyyS/8PjnVVRcevYKDq5Fgj9LKmvg/pty6cUy6bz/rO4l0ZBFogVpCw6HmeWsL72o4WB9bfUguwRFm9gRaQzbmGW9tpC3uzRhfiJKiInZ8/lZQLAlfYYfcmF0R6xR8lx3HBXAwAAcXBDpPUTVBY+jgWCnp7SZ/Pb8uB4qudR/HW6sLKo3Lb0hkKHFDk+99e4120oF0nqD+y8804cX4O+9qOFgaEcM5kT+RQpC8dxfx4ODs/tlU1xpTXmyYNb3BjSY8XRg4lFYk7f7aVxAAAg3CI++QSVBeXeAAAQxpXQlVtqHOizuL1ZjuPozVWrKc1sMoLAFyUB/+D7J6TCltohVJbUe3A1bVvVCAV3YiR6sXTchTj0tR/1DYzZMMt2snAc92IiGFOTMRri0NQqs8mMDombLMNbr6NmzyNTbT8kJnwrk5+j8ijeHA3foxHzHCemLGxZdjoqeUIQpeP9z7cG4m0hGmDKC6wX2wY87mHU9xGbgsRzvaIQnXzsa6lcEu08uPyDBz2izpq2rVrw+ZNxs1Rdn38RXSV97UemgcknFH0nZr+VFZjjc2reKqmLW3i4qyEzr2R3dxsl8hBGy5JX6iq8l5D3SfHDjmifboDZzvu7gwZxWQww2ydPniYdb0OsrCVEIsrCu6Yj3hXIyQwAjfG2y+lqKOdNAa0ACHGW6giubg2Q9p3ky0m7qLMwU27kq+hkJG3RtG3VInQ50R4ywrs0fjpW2oi+9iPTwOSD1iSJTkQWJZRTw6dxiOFxD6eFpMS7NI4EwmavlPA38XE3flb3N1NB73J0B7ztYsmFy/UEQHS8GdFxpezzyRXkajEcdsS8rGJl8bhH+FSlgfBVc/i4QOnl26K3yHELj3qMlpx1PmWIpYPJP1LTxoMOY7HbSAH65uBq2bZqESjLMcd9RrTPk2Mxxkx11dV+1Dew8uNmACi70qH0EEh7W0LcGP+6zZTWN7bnWkJ+YpAM6vP9QX5BHH58FKEsY303HFU3Ru80QygZOhAIa5Kl8TsonzCUf7SnPiMPH/LFwpSFD3qLKcukqysoKwZT9N6AHMfaDxkA4M2iKrE79K8vmAzE4KxH+CGa3goAJps9dvwsJOdKJ1yqiHBGoh7zhjRrW5XY9TyNqwvepce2DBNhPiIyj1c/+1HbwPiJfIqmC/CdPtGcmgBTabdFqhWaHg0AYHgksjYVysE1HLLzDc8Pvn798X/yxSYGbv28hKTZYFC5vKFr2/P0esegq8fZ6PyUCXA+jzvrZznBhfVCYWnk5Zlx3Ra6e8KUBa0iAQCF5XUU9ZivBO3zjrjuFudno2//sfrq+qY/5g3ca70EAGKrENM+z/EM04E3iqLt6mx+MGe56Ox70bYRWnsmTkKEpuy+mOCV5ZlM34yqaNS26hBg3g1lr9nJaxEX8XnXKOpBbWkxKiDxGtfLflQ3sGBQXDybPia8Og88eRnre9ZJlgDAH59HdpmHuhtR/Y2Wo2g1zIgD0XI5YboZYE4ENyk3vN/eTVFUXXlhaAG6AEpWK6+7duU3v2N2XqBaZecXW8xm4cJ6aI645WhR+0f15eFvlL0Vtm9erQZxLNZskiS777rENCV4B9srqFMT/YQWp4aFa6MubgRf+z/u/LW0OF94LVOGrfPLMBcgGtElNg1cLQQrP+mzioJGbZsk22tzJEnaMkwSxhOBxHx8vexHdQNDUxxO1n6k9MDak1kQs+tEb/DrBxtMGb2CKeOdH74rmLYDAIYzdR8KnYfBYSZhXNoKG2Z5n09ZLUhcgDBabva4+P3GTx8zAoDNfsZHsxy7nWNBMThLxEiFDyFVNXRFSKj6u4L0NJ0HgEut91Q8Z7X9EADx0J34KqQqIEgt02vHGS3adr+hi/2obWDBKQ4J7M/tXRglAMxHTqkYzkMzrc41fBrjO5amKEo4QEH4N9epx3P8v4x/k6KomKvTLs9Px9yAQX1lQUtvGtKz1VoTC3URdZzlHCS0dr/8QLXqqN62+5DU24/qBsZuLRBJ9IA6rpQBwOCsWjLHnjpiNpiS2nUgATTZyWx94ZEh3vQz+TScyzNm5m3qv/fQjlVvZeHUbtv9SYrtR3UDQ32EhKUhwPjtNpNai6i7H34KQMScNKgpWu2RODPUTRDGZHZRCJ7HdZswWtyeVOePxOLHkJfQqu/2m2q17X4mZfajgYGxZdnpSfaA6M3VoxZj8rNJ6c1Vq8mgaCdytdBw99WZkb6D6RnJPLPnU/ffyLTuD1nhOH6xK+Kw+OZTKSL5tt3/pMB+VDEw79Jji5E4+e4n6N+F0R6TtSD5HpB/c7XAanH2Jb7ZFuP3Fh3N1Gu7Lm33dd70uH9RZB8Yc8cvGgnb3/7+qfI66TW4UkxwsSud9xsKkkTbvjJoaT+qGRiK+JY3dHEc53GP5eb9PFbcNxECjP+DuvKqho4EhkUr048cxY4xtyd+UW1IwY7xgdG7f1C8L+/i7PicPnOaJQhOLbEW6V0RnkTa9lVDE/tR0cAYv/d8cW5uYcn5isprNztVT0dcX57+s/J9nb/o/lLfXXRSoCw/HXqvV4CMaR0YDAYriwLQ7Ie9FcUxGIwIWFkUgJb8S8xjvzw/ze+Pw3Fs17U6NNWlsLyO36IFg/nJgJVFAWiJlojNLmTAXq9wFJacIUkyOzvfs838oa2OMFoeTa9wHLc2P3nCfvonnPmG+dsEK4sUCxOuDJMBCOMnfUMcx7kfdAEYlhRNMuO4lcnPO1zBOaAs7fvgd5fSDWEbfa7PDipXKwxmX4OVRYLg/i+I/OJSq8WYdbI2uhy/0GE0RaTzfmencAJjT9N5wpgVpk4BX2fnfc3vBoNJIVhZJKCPGSKV4t5TxQkCk/3tf1oNztxltj3pBsj5h1phRJDdWmiNWjEQg3mlwcoiRc/754WyIr13nxgBZvvML+y9Aw+oBwO5tgxrQen2tvejf/0i9D17493zEdPbMZhXHaws0gRG73aSJEleuDq3uJbwWVja193uJEmSz6RaX5iwF9lJksw+eqSfwk4WzE+N/wfwfCWPX34fAAAAAABJRU5ErkJggg==" alt="" width="209" height="33" />。在Beta分布中，可以计算得到，E(x) = α / (α+β)，D(x) = αβ / (α+β)²(α+β+1)。

2）根据给出的样本，按照计算样本的原点矩。通常它的均值mean用 aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCAAfABoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD7F/4YmsP+izfGr/wvbuj/AIYmsP8Aos3xq/8AC9u6+jWGQRkjPcV8Jz+IfH3w9/4KJaB8M9f+JXiW/wDh74n0aXU9EtpZYFYXKK5aCSVYgzKPIlIGQcPGCTzkWrSB6K56/wD8MTWH/RZvjV/4Xt3R/wAMTWH/AEWb41f+F7d0vx6fxh8WfHmkeBfhX401PwlqmlzpceJ9esBHLa6daspK27I6ESXUuVZUBGxBvfAZA/dW/wADb+G3ijf4p+Pp3RQrSvfWoZyByxAtgMnrwAKFqD0PU6/OD/gqf4vh0rxH8OvGHhSbUB4m+HGrJLq+r6VEjppUF1s2RyO+V85zGpWIhvlYlgFdd3pn7R//AAUY8DeDfHlt8KvDXiGTT/FN1qP9lat4im0yaW38Pjdtd1jKZuJuyBQ0eWDMxAKnY/bP8N/DP4O/sO+N/CmqXMmnafqdnKLS5uI5bq51DVz+/ilnkVWZpZJ40LSPgc8kAACW7Ln7FJa8r6n0l8MvBvh/wN4L0/TvDKFtLdftQupJTLNeSSfO9xLK3zSSSElmduSTXU18df8ABNf9q7w78bvgh4Y8GSX8p8eeF9LWz1Cykgkw0EJWKKcS7djbk8vI3bt27jGCfsWtJKzM4u6P/9k=" alt="" width="18" height="19" /> 表示，方差var用 aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCAAfACADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD9U6K8w/ad+JGqfCD9n3x94y0S3W51fRtJmubRXXcqyAYV2Xuqk7iO4U14z+yV8JvAvxe/Z98IePNS1PU/FvjDXbBbvU/FMms3K6hDfHPnxxSxyA24ik3Rqke0AKOOTkWt/IOx9P8AirUtR0nw/eXOkaYNY1RVC2tk03kpLKxCrvkw2xASCzBWIUMQrEYPkfw4+L3j1PjbdfDL4jaBoltqE+iN4h0rWPDNzNLazQJMkMsMqTKHSRWlQgjKsG7EYrF+B8upfAP4SePvE3xS8V6prnk+ItRkGq6ojSXT2MEv2S1RY1UZLrArBUX5mlJGd2TL8EfjN4B+JnxJu9UsdWk1jxxq9mIhaw2FysWladCWdYTI8ap9+TLsDl5HUDKomBb/ANdge39dz3HVpNH1iWfw1qIt7039lK02nToHWa2OI5NykYKneFIPXJ96/NLxXp3iX/glJ8bbbXdBa71v9nTxjfiO90p2Mj6TcEZIQn+NVBKN/wAtEQo3zIr19d+INN+Kem/tW3XjfSNDtdd+Hlr4fh8PXOmRX8cWoyTmQ3JuoEk2xFV3pGyvIhIyQDgZ4/8Aaa8Fax+254V0X4e6BpU+j+DzrEF94g8TalJADFDECfs9tCjtI0z7h8zKqKB1bOAle6a3/wCD/kN21T2/4B9Z2t1DfWsNzbyLLBMgkjkU5DKRkEexBqWoLGyg0yxt7O2jEVtbxrFFGOiqowB+AFT1TtfQlXtqf//Z" alt="" width="20" height="19" />表示。（另外提一句，求aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCAAfACADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD9U6K8w/ad+JGqfCD9n3x94y0S3W51fRtJmubRXXcqyAYV2Xuqk7iO4U14z+yV8JvAvxe/Z98IePNS1PU/FvjDXbBbvU/FMms3K6hDfHPnxxSxyA24ik3Rqke0AKOOTkWt/IOx9P8AirUtR0nw/eXOkaYNY1RVC2tk03kpLKxCrvkw2xASCzBWIUMQrEYPkfw4+L3j1PjbdfDL4jaBoltqE+iN4h0rWPDNzNLazQJMkMsMqTKHSRWlQgjKsG7EYrF+B8upfAP4SePvE3xS8V6prnk+ItRkGq6ojSXT2MEv2S1RY1UZLrArBUX5mlJGd2TL8EfjN4B+JnxJu9UsdWk1jxxq9mIhaw2FysWladCWdYTI8ap9+TLsDl5HUDKomBb/ANdge39dz3HVpNH1iWfw1qIt7039lK02nToHWa2OI5NykYKneFIPXJ96/NLxXp3iX/glJ8bbbXdBa71v9nTxjfiO90p2Mj6TcEZIQn+NVBKN/wAtEQo3zIr19d+INN+Kem/tW3XjfSNDtdd+Hlr4fh8PXOmRX8cWoyTmQ3JuoEk2xFV3pGyvIhIyQDgZ4/8Aaa8Fax+254V0X4e6BpU+j+DzrEF94g8TalJADFDECfs9tCjtI0z7h8zKqKB1bOAle6a3/wCD/kN21T2/4B9Z2t1DfWsNzbyLLBMgkjkU5DKRkEexBqWoLGyg0yxt7O2jEVtbxrFFGOiqowB+AFT1TtfQlXtqf//Z" alt="" width="20" height="19" />时，通常用n-1为底。这样是想让结果跟接近总体的方差，又称为无偏估计）

3）让总体的原点矩与样本的原点矩相等，解出参数。所得结果即为参数的矩估计值。这里有，mean = E(x) = α / (α+β)，var = D(x) = αβ / (α+β)²(α+β+1)。于是乎，我们可以求得α，β：

α = [mean*(1-mean)/var - 1] * mean

β = [mean*(1-mean)/var - 1] * (1-mean)

2. Fixed-point iteration

首先构造出似然函数，然后利用Fixed-point iteration来求得似然函数的最大值。

1）首先给出参数的一个初始值（通常可以使用矩估计得到的结果作为初始值）。

2）在初始值处，构造似然函数的一个紧的下界函数。这个下界函数可以求得其最大值处的闭式解，将此解作为新的估计用于下一次迭代中。

3）不断重复上述（2）的步骤，直至收敛。此时便可到达似然函数的stationary point。如果似然函数是convex的，那么此时就是唯一的最优解。

其实Fixed-point iteration的思想与EM类似。

首先给出两个不等式关系：

1）

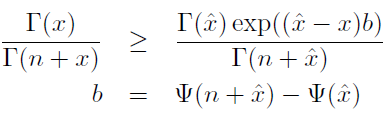
2）

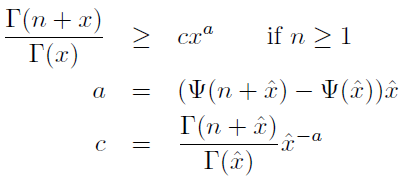
由此可以得到对数似然函数的一个下界：

想要得到此下界函数的最大值，可以分别对α，β求偏导，并令之等于零，此时便得到α和β各自的迭代公式：

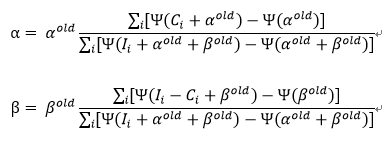
由此，每次迭代，参数都会达到此次下界函数的最大值处，同时也就使得对应的似然函数值也相应地不断增大，直至收敛到似然函数的最大值处。

3. EM

通过将概率参数作为隐含变量，任何估计概率参数的算法都可以使用EM进一步变成估计个数参数的算法。

（1）E-step：计算出隐含变量p在已观测数据（观测到的每个类别发生的次数，以及每个类别的超参数值的上一轮迭代的取值）下的后验分布，便可以得到完全数据的对数似然函数的期望值。

（2）M-step：对E-step中的期望值求最大值，便可得到相应的超参数的本轮迭代的更新值。

（3）不断重复地运行E-step和M-step，直至收敛。

回来我们这里的问题上，在有了观测到的每个类别发生的次数，以及每个类别的超参数值的上一轮迭代的取值后，隐含变量p的后验分布为：

而此时的完全数据的对数似然函数的期望为：

其中，

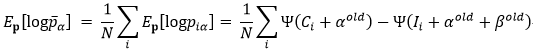
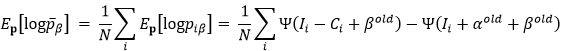
于是乎，我们可以对完全数据的对数似然函数的期望求最大值，从而得到α，β的更新值，有很多方法，直接求偏导，梯度下降，牛顿法等。

但是呢，此时我们并不需要非常精确地求得它的最大值，而是仅仅用牛顿法迭代一次。相比于精确地求得最大值，这种方法在每次迭代时只有一半的计算量，但是迭代次数会超过两倍。

牛顿法的迭代可见：

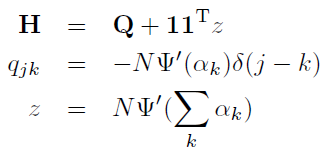
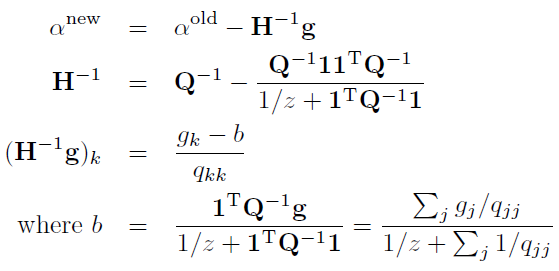
3. 代码实现

 #!/usr/bin/python

 # coding=utf-8

 import numpy

 import random

 import scipy.special as special

 import math

 from math import log

 class HyperParam(object):

     def __init__(self, alpha, beta):

         self.alpha = alpha

         self.beta = beta

     def sample_from_beta(self, alpha, beta, num, imp_upperbound):

         sample = numpy.random.beta(alpha, beta, num)

         I = []

         C = []

         for click_ratio in sample:

             imp = random.random() * imp_upperbound

             #imp = imp_upperbound

             click = imp * click_ratio

             I.append(imp)

             C.append(click)

         return I, C

     def update_from_data_by_FPI(self, tries, success, iter_num, epsilon):

         '''estimate alpha, beta using fixed point iteration'''

         for i in range(iter_num):

             new_alpha, new_beta = self.__fixed_point_iteration(tries, success, self.alpha, self.beta)

             if abs(new_alpha-self.alpha)<epsilon and abs(new_beta-self.beta)<epsilon:

                 break

             self.alpha = new_alpha

             self.beta = new_beta

     def __fixed_point_iteration(self, tries, success, alpha, beta):

         '''fixed point iteration'''

         sumfenzialpha = 0.0

         sumfenzibeta = 0.0

         sumfenmu = 0.0

         for i in range(len(tries)):

             sumfenzialpha += (special.digamma(success[i]+alpha) - special.digamma(alpha))

             sumfenzibeta += (special.digamma(tries[i]-success[i]+beta) - special.digamma(beta))

             sumfenmu += (special.digamma(tries[i]+alpha+beta) - special.digamma(alpha+beta))

         return alpha*(sumfenzialpha/sumfenmu), beta*(sumfenzibeta/sumfenmu)

     def update_from_data_by_moment(self, tries, success):

         '''estimate alpha, beta using moment estimation'''

         mean, var = self.__compute_moment(tries, success)

         #print 'mean and variance: ', mean, var

         #self.alpha = mean*(mean*(1-mean)/(var+0.000001)-1)

         self.alpha = (mean+0.000001) * ((mean+0.000001) * (1.000001 - mean) / (var+0.000001) - 1)

         #self.beta = (1-mean)*(mean*(1-mean)/(var+0.000001)-1)

         self.beta = (1.000001 - mean) * ((mean+0.000001) * (1.000001 - mean) / (var+0.000001) - 1)

     def __compute_moment(self, tries, success):

         '''moment estimation'''

         ctr_list = []

         var = 0.0

         for i in range(len(tries)):

             ctr_list.append(float(success[i])/tries[i])

         mean = sum(ctr_list)/len(ctr_list)

         for ctr in ctr_list:

             var += pow(ctr-mean, 2)

         return mean, var/(len(ctr_list)-1)

 def test():

     hyper = HyperParam(1, 1)

     #--------sample training data--------

     I, C = hyper.sample_from_beta(10, 1000, 10000, 1000)

     print I, C

     #--------estimate parameter using fixed-point iteration--------

     hyper.update_from_data_by_FPI(I, C, 1000, 0.00000001)

     print hyper.alpha, hyper.beta

     #--------estimate parameter using moment estimation--------

     hyper.update_from_data_by_moment(I, C)

     print hyper.alpha, hyper.beta

4. 参考文献

1. Click-Through Rate Estimation for Rare Events in Online Advertising

2. Estimating a Dirichlet distribution

本文由笨兔勿应所有，发布于http://www.cnblogs.com/bentuwuying。如果转载，请注明出处，在未经作者同意下将本文用于商业用途，将追究其法律责任。