POJ 1631 Bridging signals（LIS O(nlogn)算法）

Bridging signals

Description

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task? 

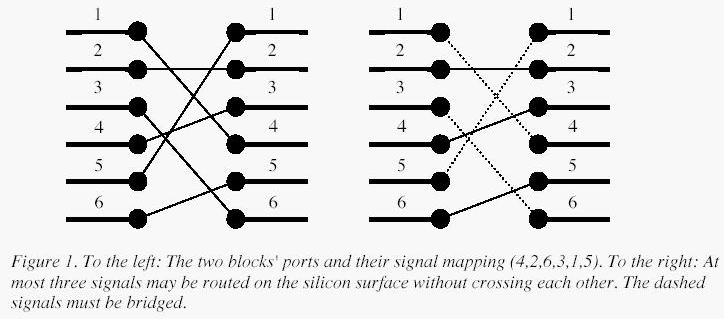
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number specifies which port on the right side should be connected to the i:th port on the left side.Two signals cross if and only if the straight lines connecting the two ports of each pair do.

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

题目大意：求最长上升子序列，序列长度最大为40000。

分析：如果用一般的LIS算法，时间复杂度高达n^2。这里引用《入门经典》复杂度为O(nlogn)的方法。
　　假设已经计算出的两个状态 a 和 b 满足Aa < Bb 且d(a)==d(b),则对于后续所有状态 i（即i>a且i>b）来说，a并不会比b差——如果b满足Ab < Ai的条件，a也满足，且二者的d值相同；但反过来却不一定了。换句话说，如果我们只保留a，一定不会丢失最优解。
　　这样，对于相同的d值，只需要保留A最小的一个。我们用g(i)表示d值为i的最小状态编号。根据上述推理证明
　　g(1)<=g(2)<=g(3)<=...<=g(n)
　　上述的g值是动态改变的。对于一个给定的状态i，我们只考虑在i之前已经计算过的状态j（即j<i）。在给定状态i时可以用二分查找得到满足g(k)>=Ai的第一个下标k，则d(i)=k,此时Ai<g(k),而d(i)=k,所以更新g(k)=Ai。（话说看的不是很明白）

 for(i=1; i<=n; i++) g[i] = INF;
        for(i=0; i<n; i++)
        {
            int k = lower_bound(g+1,g+n+1,A[i]) - g;
　　　　　　d[i]=k;
            g[k] = A[i];
        }
代码如下：

 # include<cstdio>
 # include<iostream>
 # include<algorithm>
 using namespace std;
 # define INF 0xffffff
 int n;
 int g[],A[];

 int main()
 {
     int i,T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         for(i=; i<n; i++)
             scanf("%d",&A[i]);
             int ans = ;
         for(i=; i<=n; i++)  g[i] = INF;
         for(i=; i<n; i++)
         {
             int k = lower_bound(g+,g+n+,A[i]) - g;
             g[k] = A[i];
             if(k>ans)
             ans = k;
         }
         printf("%d\n",ans);
     }
     return ;
 }

LIS nlogn算法大罗列！

网上有这一方面的总结 //n是原序列长度，a[]是原序列，D是a[]的值域大小

1. f[i]表示a[i]结尾的LIS长度，f[i] = max{f[j]}+1 : a[j]<a[i]

1.1 维护一个以a的值为下标，以f的值为值的树状数组优化转移。O(n log D)

1.2 g[x]表示长度为x的所有LIS中最小的末尾的值，可证g[x]单调递增，二分查找转移。O(n log n)

1.3 维护一个“最优”的LIS q，每次将q关于a[i]的lower_bound更新为a[i]，同时转移。O(n log n)

1.2代码如下：

 #include <iostream>
 using namespace std;

 int a[];
 int dp[];
 int b[], blen;
 int n;

 int main() {
     int ca,i;
     scanf("%d", &ca);
     while (ca--) {
         scanf("%d", &n);
         for (i = ; i <= n; ++i) {
             scanf("%d", a+i);
         }
         memset(b,,sizeof(b));
         memset(dp,,sizeof(dp));

         int left, right, mid;
         blen = ;
         int res = ;
         for (i = ; i <= n; ++i) {
             left = ;
             right = blen;
             int num = a[i];
             while (left <= right) {
                 mid = (left + right)/;
                 if (b[mid] < a[i]) {
                     left = mid + ;
                 }
                 else {
                     right = mid - ;
                 }
             }
             dp[i] = left;
             b[left] = a[i];
             if (blen < left)
                 blen = left;
             if (res < dp[i])
                 res = dp[i];
         }
         printf("%d\n", res);
     }
     return ;
 }